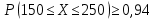Многоугольник распределения.171. В партии из шести деталей имеется четыре стандартных. Наудачу отобраны три детали. Составить закон распределения дискретной случайной величины X — числа стандартных деталей среди отобранных.

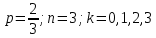
k	0	1	2	3
P(X = k)	0,037037	0,222222	0,444444	0,296296

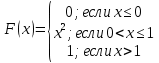
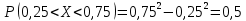
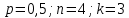
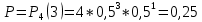
257. Случайная величина X задана функцией распределения:Найти вероятность того, что в результате четырех независимых испытаний величина X ровно три раза примет значение, принадлежащее интервалу (0,25, 0,75).Сначала найдем вероятность при одном испытании.Далее применяем формулу Бернулли.Ответ: 0,25261. Дискретная случайная величина задана законом распределения

X	3	4	7	10
P	0,2	0,1	0,4	0,3

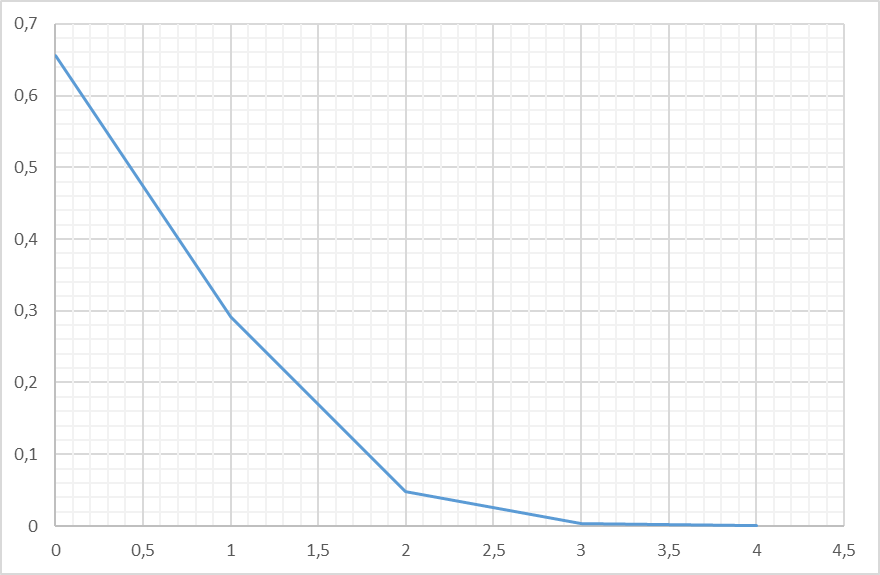
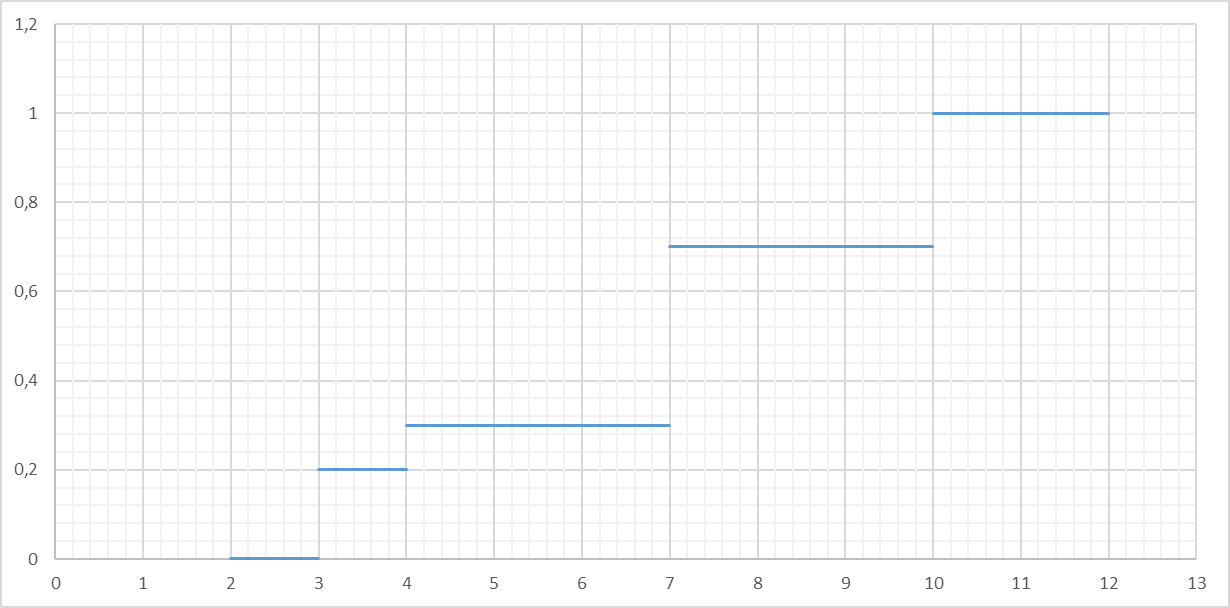
Найти функцию распределения и построить ее график.Дополним таблицу вероятностью с нарастающим итогом.

X	3	4	7	10
P	0,2	0,1	0,4	0,3
С нарастающим итогом	0,2	0,3	0,7	1

---

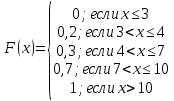
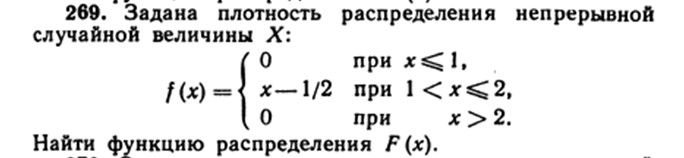
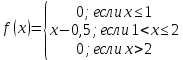
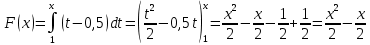
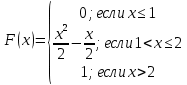
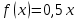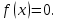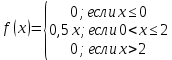
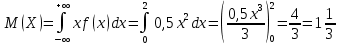
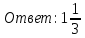
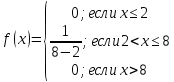
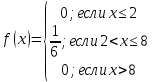
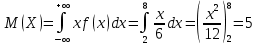
276. Случайная величина X задана плотностью распределения в интервале (0; 2); вне этого интервала / Найти математическое ожидание величины X.314. Найти математическое ожидание случайной величины X, распределенной равномерно в интервале (2, 8).Ответ: 5322. Математическое ожидание нормально распределенной случайной величины X равно а = З н среднее квадратическое отклонение ???? = 2. 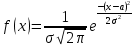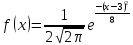Написать плотность вероятности X.323. 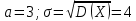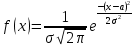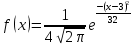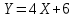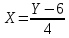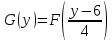Написать плотность вероятности нормально распределенной случайной величины Х, зная, что М{Х) = 3; D(X)=16.а)б)

---

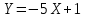
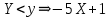
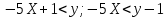
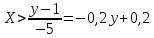
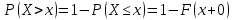
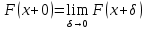
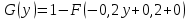
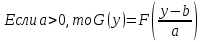
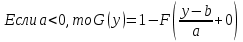
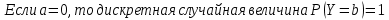
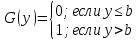
гдев)а)

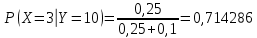
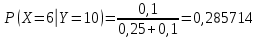
x	3	6
P(X = x)	0,714286	0,285714

б)

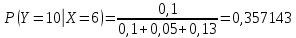
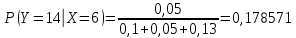
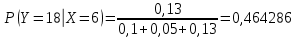
x	10	14	18
P(X = x)	0,357143	0,178571	0,464286

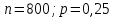
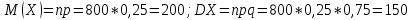
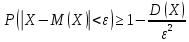
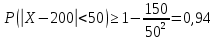
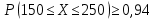
244. Вероятность появления события в каждом испытании равна 1/4. Используя неравенство Чебышева, оценить вероятность того, что число X появлений события заключено в пределах от 150 до 250, если будет произведено 800 испытаний.Согласно неравенству Чебышева:Ответ:

---

Смотрите также файлы

• Пропишите принципы организации индивидуальной логопедической работы с детьми. Цель.docx

• Программа среднего профессионального образования 46. 02. 01 Документационное обеспечение управления и архивоведение Дисциплина Управление персоналом (3 семестр) Практическое задание 1.doc

• Вещные права субъектов предпринимательской деятельности Вопрос Общая характеристика вещных прав предпринимателя.pdf

• 1. Морской транспорт и его значение, характеристика. Структурнофункиональная характеристика етс.rtf

• Информационнокоммуникационные технологии для профессиональной деятельности ответы синергия с ответами.docx