Файл: Методические указания к практическим занятиям для студентов направления подготовки.docx
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 10.01.2024
Просмотров: 152
Скачиваний: 1
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
СОДЕРЖАНИЕ
ПОСТРОЕНИЕ ПАСПОРТА ОБЪЕМНОЙ ПРОЧНОСТИ ГОРНОЙ ПОРОДЫ
Расчет нормальных тангенциальных напряжений на неровном контуре выработки кругового очертания
Приложение 1 – исходные данные для расчетно-графической работы №1
Приложение 2 – исходные данные для расчетно-графической работы №2
Приложение 3 – исходные данные для расчетно-графической работы №3
Приложение 4 – исходные данные для расчетно-графической работы №4
Приложение 5 – исходные данные для расчетно-графической работы №5
Расчет параметров напряженно-деформированного состояния массива горных пород в окрестности горной выработки кругового очертания
Цель работы: рассчитать величины и оценить закономерности распределения компонент напряжений и смещений в окрестности незакрепленной горной выработки кругового очертания, расположенной в изотропном линейно-упругом массиве.
Исходные данные:
Рассчитать компоненты напряжений σR, σθ, σz и τRθ в изотропном упругом массиве пород на контуре и в окрестности незакрепленной выработки кругового очертания при коэффициентах бокового распора λ=1 и λ=λ2. Для этих же условий рассчитать величины смешений контура выработки ur и uθ.
Для построения эпюр при λ=λ2 рассмотреть направления с угловой координатой θ=0, 45 и 900. Безразмерный радиус r=R/R0 (R – текущий радиус; R0 – радиус выработки) принимать в диапазоне от 1 до 12 (не менее 10 точек).
Расчетные положения:
В рамках данного расчетно-графического задания предполагается использование линейно-упругой модели массива пород. Для этой модели коэффициент бокового распора следует определять согласно гипотезе Динника:
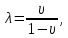
где
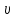 – коэффициент Пуассона массива горных пород.
– коэффициент Пуассона массива горных пород.Для определения компонент напряженного состояния в окрестности горной выработки воспользуемся решением задачи Кирша из теории упругости:
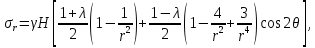
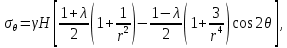
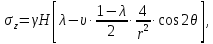
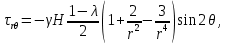

γH
где
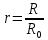 – приведенное расстояние до рассматриваемой точки массива в окрестности горной выработки
– приведенное расстояние до рассматриваемой точки массива в окрестности горной выработки
;
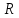 - расстояние до рассматриваемой точки массива в окрестности горной выработки;
- расстояние до рассматриваемой точки массива в окрестности горной выработки; 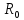 – радиус горной выработки;
– радиус горной выработки; 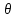 – угловая координата (см. рисунок 2).
– угловая координата (см. рисунок 2).








σR
σθ
τRθ
λγH
θ
2R0
θ=450
θ=900
θ=0
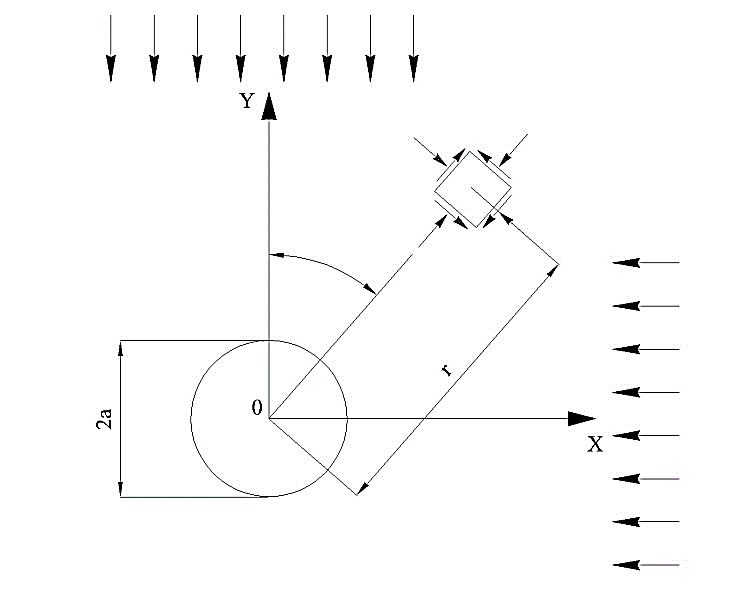
Рисунок 2 – Расчетная схема к задаче Кирша
Для построения эпюры распределения нормальных тангенциальных напряжений на контуре выработки необходимо задать приведенное расстояние до рассматриваемой точки массива в окрестности горной выработки равным 1 и преобразовать соответствующую формулу решения Кирша в следующий вид:
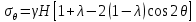 .
.Смещения точек массива в окрестности горной выработки следует определять по следующим формулам:
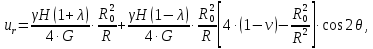
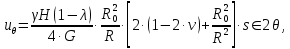
где
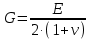 – модуль сдвига массива горных пород в окрестности горной выработки;
– модуль сдвига массива горных пород в окрестности горной выработки; 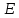 – модуль деформации массива горных пород в окрестности горной выработки.
– модуль деформации массива горных пород в окрестности горной выработки.Для построения эпюры распределения смещений на контуре выработки следует подставить в вышеприведенные формулы смещений
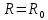 .
.Последовательность выполнения расчетно-графической работы:
-
Выполняется построение эпюр распределения ненулевых компонент напряжений для случая λ=1. -
Выполняется построение эпюры распределения нормальных тангенциальных напряжений на контуре незакрепленной горной выработки кругового очертания для случая λ=1. -
Выполняется построение эпюр распределения смещений породного контура выработки кругового очертания для случая λ=1. -
Выполняется построение эпюр распределения ненулевых компонент напряжений для направлений с угловой координатой θ=0, 45 и 900 для случая λ= λ2. -
Выполняется построение эпюры распределения нормальных тангенциальных напряжений на контуре незакрепленной горной выработки кругового очертания для случая λ= λ2. -
Выполняется построение эпюр распределения смещений породного контура выработки кругового очертания для случая λ= λ2.
- 1 2 3 4 5 6 7 8 9
Определение размеров зоны предельного состояния вокруг выработки в анизотропном (слоистом) массиве пород
Цель работы: рассчитать значения и оценить зависимость размеров зоны предельного состояния вокруг горизонтальной выработки от степени анизотропии массива пород и коэффициента бокового распора λ.
Исходные данные: незакрепленная протяженная выработка кругового очертания расположена на глубине H от поверхности в анизотропном (слоистом) упругопластическом массиве. Рассчитать и оценить зависимость радиуса зоны предельного состояния вокруг горизонтальной выработки от коэффициента бокового распора λ. Сравнить полученные зоны предельного состояния пород в анизотропном массиве со средними радиусами зон предельного состояния в изотропном массиве с крайними величинами сцепления (
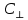 и
и 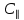 ) и λ=1.
) и λ=1.Расчетные положения:
Испытания образцов горных пород при одноосном сжатии перпендикулярно и параллельно слоистости показывают, что прочность в этих направлениях различна.
Для оценки степени анизотропии введем коэффициент
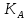 анизотропии, равный отношению предела прочности на сжатие перпендикулярно слоистости
анизотропии, равный отношению предела прочности на сжатие перпендикулярно слоистости 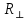 к пределу прочности параллельно слоистости
к пределу прочности параллельно слоистости 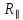 . Для пород средней устойчивости значение этого коэффициента изменяется от 2,5 до 1,77, для неустойчивых - от 2,66 до 2,57, а для весьма неустойчивых - около 3,0.
. Для пород средней устойчивости значение этого коэффициента изменяется от 2,5 до 1,77, для неустойчивых - от 2,66 до 2,57, а для весьма неустойчивых - около 3,0.Аппроксимацию сцепления в массиве пород около выработки представим зависимостью:
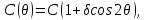
где
 - угловая координата точки относительно горизонтальной оси Y.
- угловая координата точки относительно горизонтальной оси Y.При
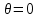 и 90 получим соответственно:
и 90 получим соответственно: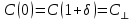 и
и 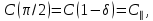
где
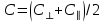
- среднее сцепление;
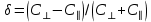 - показатель анизотропии;
- показатель анизотропии;  ,
,  - соответственно сцепление в массиве при действии нагрузки перпендикулярно слоистости (бок выработки) и параллельно слоистости (кровля выработки).
- соответственно сцепление в массиве при действии нагрузки перпендикулярно слоистости (бок выработки) и параллельно слоистости (кровля выработки).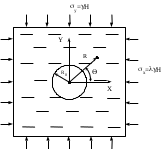
Для протяженной выработки круглого сечения расчетная схема может быть представлена отверстием в невесомой плоскости (рисунок 3), нагруженной на бесконечности напряжениями и , где - коэффициент бокового распора; Н – глубина заложения выработки; - объемный вес пород в массиве.
Рисунок 3 – Расчетная схема к определению размеров зоны предельного состояния
Решение плоской упругопластической задачи показывает, что безразмерный радиус
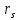 зоны неупругих деформаций вокруг выработки имеет вид:
зоны неупругих деформаций вокруг выработки имеет вид: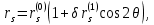
где для нулевого приближения (без учета анизотропии):
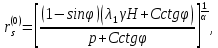
для первого приближения (с учетом анизотропии):
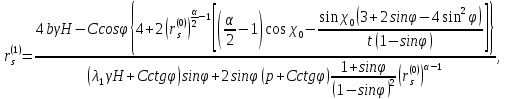
здесь
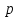 - отпор крепи по контуру выработки;
- отпор крепи по контуру выработки;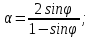
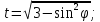
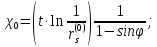
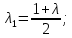
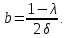
Последовательность выполнения расчетно-графической работы:
-
Выполнить расчет радиуса зоны предельного состояния вокруг горной выработки в изотропном упругопластическом массиве горных пород в нулевом приближении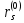 при
при 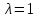 с учетом отпора крепи.
с учетом отпора крепи. -
Выполнить расчет поправки радиуса зоны предельного состояния вокруг горной выработки в слоистом упругопластическом массиве горных пород в первом приближении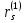 при заданном значении
при заданном значении 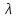 с учетом отпора крепи.
с учетом отпора крепи. -
Выполнить построение зоны предельного состояния вокруг горной выработки.