ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 10.01.2024
Просмотров: 13
Скачиваний: 1
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
Задание Д12. Исследование плоского движения твердого тела.
Определить значение постоянной силы
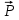, под действием которой качение без скольжения колеса массой m носит граничный характер, т.е. сцепление колеса с основанием находится на грани срыва.Найти также для этого случая уравнение движения центра масс колеса С, если в начальный момент времени его координата
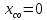и скорость 
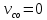.Исходные данные вариант 17:
,
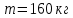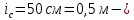радиус инерции колеса относительно оси, перпендикулярной его плоскости,
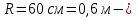радиус большой окружности,
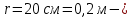радиус малой окружности,
,
,
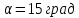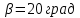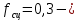коэффициент сцепления (коэффициент трения покоя), 
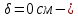коэффициент трения качения.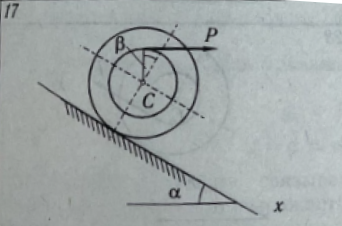
Решение
На колесо действует сила тяжести
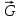, нормальная сила 
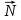, сила 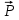, сила сцепления 
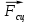. Силу сцепления направляем условно в сторону положительного направления оси х.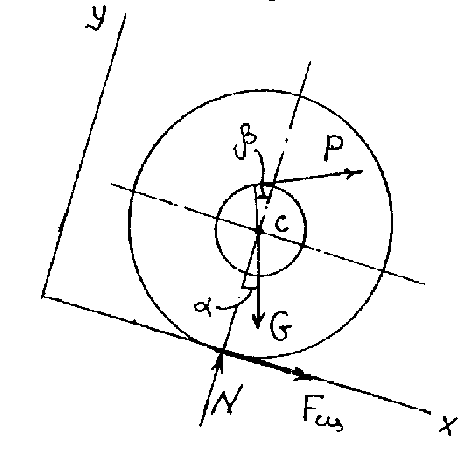 
Дифференциальные уравнения плоского движения колеса:
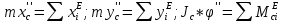
В нашем случае:
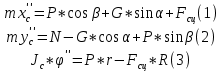
Положительным направлением отсчета угла поворота колеса принимаем направление по часовой стрелке, что соответствует движению центра колеса в положительном направлении х.
В соответствии с этим направлением по часовой стрелке принято положительным и при определении знаков моментов внешних сил в уравнении (3).
К дифференциальным уравнениям плоского движения колеса (1), (2), (3) добавим уравнения связей:
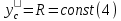
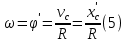
Уравнение (5) выражает условие качения колеса без скольжения.
Из (4) следует, что
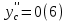.Дифференцируем (5) по времени:
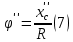
Подставляем (6) и (7) в (2) и (3) и учитывая, что
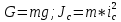
получаем:
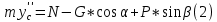
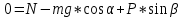
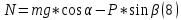
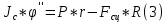
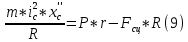
Значение
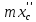из (1) подставляем в (9):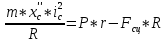
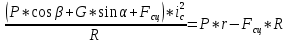
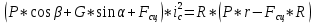
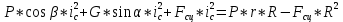
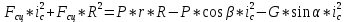
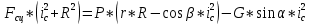
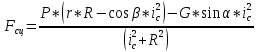
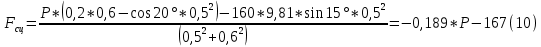
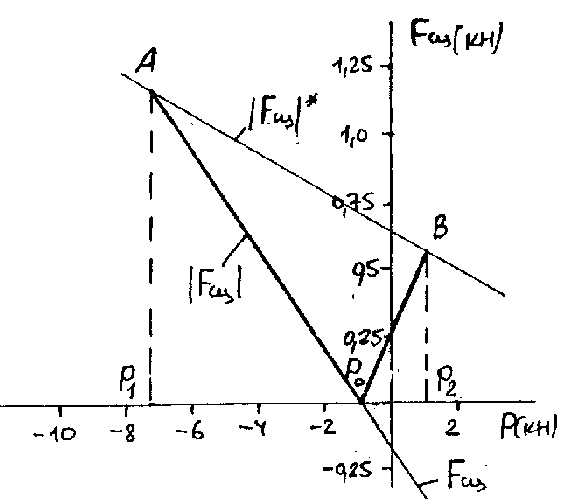
График зависимости
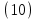показан на рисунке.График пересекает ось Р в точке
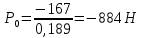.При Р >
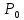
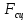> 0 – сила сцепления направлена, как показана на первом рисунке, в положительном направлении оси х. При Р <
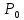
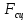< 0 – сила сцепления направлена в противоположную сторону. Модуль силы сцепления, обеспечивающий качение колеса без скольжения, подчиняется следующему ограничению:
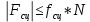(11) принимаем, что 
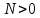всегда.Предельное значение модуля силы сцепления по выражению (11) и (8)
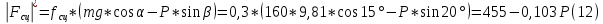
Граничные значения силы Р находим, используя (10) и (12) из условий:
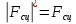
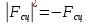
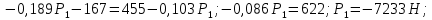
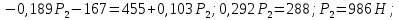
Точка А
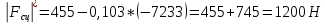
Точка В
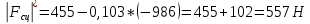
Дифференциальное уравнение движения центра колеса находим после исключения
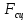из (1) и (9). Для этого умножаем уравнение (1) на R и складываем полученное уравнение с (9):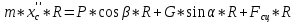
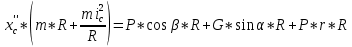
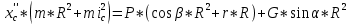
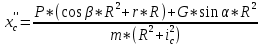
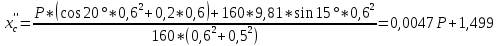
При
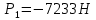
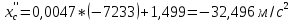
Интегрируем это дифференциальное уравнение дважды по времени:
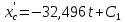
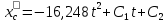
Учитывая начальные условия (
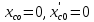) имеем 
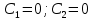.Окончательно получаем уравнение движения центра масс колеса С:
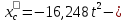колесо катиться влево;При
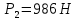
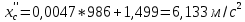
Интегрируем это дифференциальное уравнение дважды по времени:
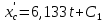
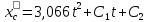
Учитывая начальные условия (
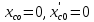) имеем 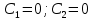.Окончательно получаем уравнение движения центра масс колеса С:
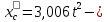колесо катиться вправо.