Файл: Контрольная работа дисциплина (модуль) наименование учебной дисциплины (модуля).docx
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 10.01.2024
Просмотров: 81
Скачиваний: 2
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
МИНИСТЕРСТВО НАУКИ И ВЫСШЕГО ОБРАЗОВАНИЯ РОССИЙСКОЙ ФЕДЕРАЦИИ ФЕДЕРАЛЬНОЕ ГОСУДАРСТВЕННОЕ БЮДЖЕТНОЕОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ ВЫСШЕГО ОБРАЗОВАНИЯ
«ДОНСКОЙ ГОСУДАРСТВЕННЫЙ ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ»(ДГТУ)Факультет «_______________________________________________________»наименование факультетаКафедра «_________________________________________________________»наименование кафедрыКОНТРОЛЬНАЯ РАБОТАДисциплина (модуль) «________________________________________________________________наименование учебной дисциплины (модуля)______________________________________________________________________________________________________________________»Направление подготовки/специальность ___________ ______________________________________коднаименование направления подготовки/специальности_____________________________________________________________________________________Направленность (профиль) ___________________________________________________________________________________________________________________________________________________________________Номер зачетной книжки ______________ Номер варианта ___1____ Группа _______________Обучающийся _______________________ _____________________________подпись, дата И.О. ФамилияКонтрольную работу проверил _____________________ _________________________________подпись, дата должность, И.О. ФамилияРостов-на-Дону 2023
, оценивает разброс опытных значений Y относительно линии регрессии.Рисунок 7. Вычисление дисперсийПолучаем и . значительно меньше , т. е. постулированная модель статистически значимо описывает процесс и может быть признана адекватной.
Рисунок 12. Произведение транспонированной матрицы Х на матрицу ХНайдем Рисунок 13. Обратная матрица матрице произведенияНайдем Рисунок 14. Произведение обратной матрицы на транспонированную матрицу ХНайдем Рисунок 15. Итоговая матрица коэффициентов ВПолучили Получаем модельВычислим значения этих функций Рисунок 16 – Вычисление значений Проверку адекватности полученной модели произведем путем сравнения двух дисперсий, одна из которых характеризует влияние на Y случайных факторов, а вторая, дисперсия адекватности , оценивает разброс опытных значений Y относительно линии регрессии.Рисунок 17. Вычисление дисперсийПолучаем меньше , т. е. постулированная модель статистически значимо описывает процесс и может быть признана адекватной.
«ДОНСКОЙ ГОСУДАРСТВЕННЫЙ ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ»(ДГТУ)Факультет «_______________________________________________________»наименование факультетаКафедра «_________________________________________________________»наименование кафедрыКОНТРОЛЬНАЯ РАБОТАДисциплина (модуль) «________________________________________________________________наименование учебной дисциплины (модуля)______________________________________________________________________________________________________________________»Направление подготовки/специальность ___________ ______________________________________коднаименование направления подготовки/специальности_____________________________________________________________________________________Направленность (профиль) ___________________________________________________________________________________________________________________________________________________________________Номер зачетной книжки ______________ Номер варианта ___1____ Группа _______________Обучающийся _______________________ _____________________________подпись, дата И.О. ФамилияКонтрольную работу проверил _____________________ _________________________________подпись, дата должность, И.О. ФамилияРостов-на-Дону 2023
ПРАКТИЧЕСКАЯ РАБОТА № 3. ОДНОФАКТОРНЫЙ РЕГРЕССИОННЫЙ АНАЛИЗ
Исследуется влияние скорости подачи на шероховатость поверхности при обработке стальной заготовки на токарном станке. В качестве постоянных параметров эксперимента используются: глубина резания t = 0,5 мм, диаметр обрабатываемой поверхности d = 50 мм, частота вращения шпинделя n = 1000 мин-1, Материал инструмента — Т15К6, материал детали — Сталь 20. Выполнить однофакторный регрессионный анализ по полученным экспериментальным данным. 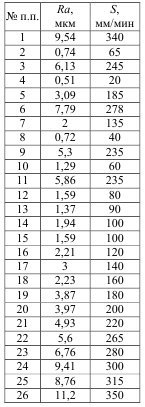Форма регрессионной зависимости Y=1 /( B0+B1*X)Рисунок 1. 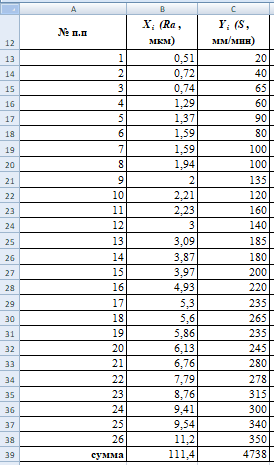Исходные зависимостиВведем эти данные в электронную таблицуРисунок 2. 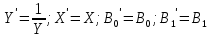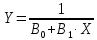Исходные данные в электронной таблицеВ результате замены переменных функция преобразовывается в линейную модель первого порядка 
.
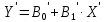Решаем следующую систему линейных алгебраических уравнений для определения неизвестныех коэффициентов уравнения регрессии B’0 и B’1:
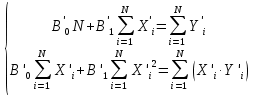
Для этого найдем 
, 
, 
, 
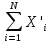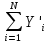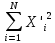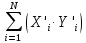в соответствующих столбцах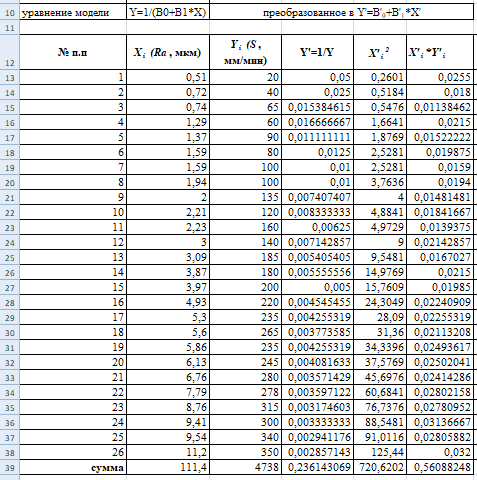
Рисунок 3. Промежуточные вычисления
Найдем коэффициенты 
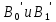
Рисунок 4. Вычисление коэффициентов 
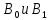
Подставим и найдем значения коэффициентов 
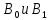
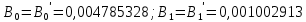
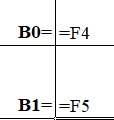
Рисунок 5 - Вычисление коэффициентов
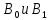
Подставим найденные значения коэффициентов в уравнение модели
Получаем
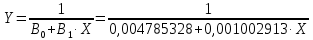
Вычислим значения этих функций 
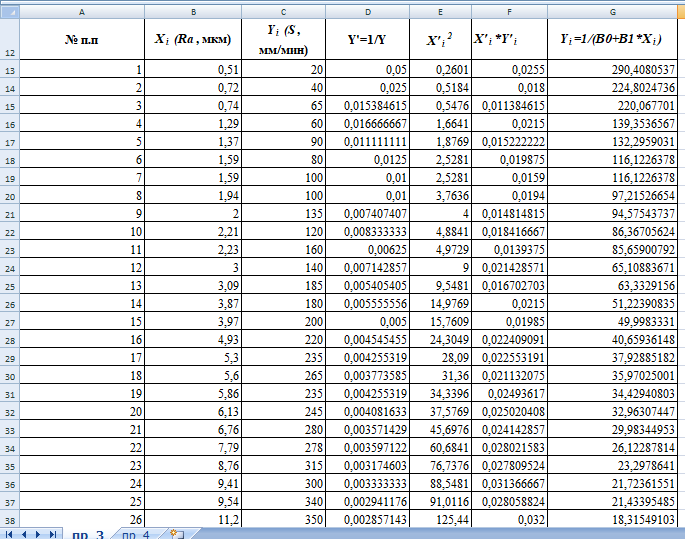
Рисунок 6 – Вычисление значений 
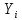
Проверку адекватности полученной модели произведем путем сравнения двух дисперсий, одна из которых 
характеризует влияние на Y случайных факторов, а вторая, дисперсия адекватности
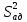, оценивает разброс опытных значений Y относительно линии регрессии.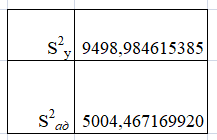Рисунок 7. Вычисление дисперсийПолучаем 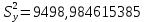и 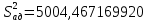. 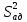значительно меньше , т. е. постулированная модель статистически значимо описывает процесс и может быть признана адекватной.
ПРАКТИЧЕСКАЯ РАБОТА № 4. МНОГОФАКТОРНЫЙ РЕГРЕССИОННЫЙ АНАЛИЗ
Исследуется влияние диаметра обработки d, скорости резания V, подачи S на шероховатость поверхности при обработке стальной заготовки на сверлильном станке. В качестве постоянных параметров эксперимента используются: материал детали — сталь 40, материал инструмента Р6М5. 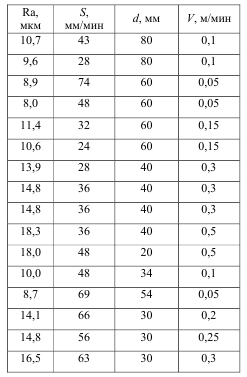Построить модель процесса с помощью многофакторного регрессионного анализа.Вид модели: Y=B0+B1*X1+B2*X2+B3*X3+B12*X1*X2 Экспериментальные данные представлены в таблице.Рисунок 8. 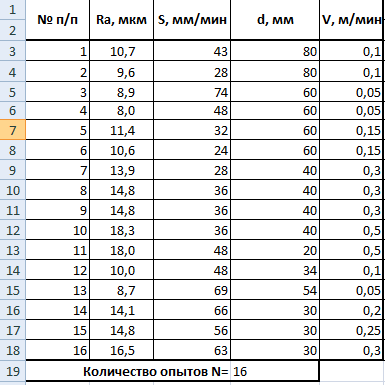Исходные зависимостиВведем эти данные в электронную таблицуРисунок 9. 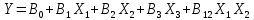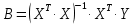Исходные данные в электронной таблицеИмеем функцию полинома первого порядка с учетом взаимного влияния факторов .Найдем матрицу оценок коэффициентов регрессииИмеем матрицу X с дополнительным единичным столбцом и матрицу YРисунок 10. 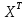Матрица Х и YНайдем Рисунок 11. 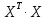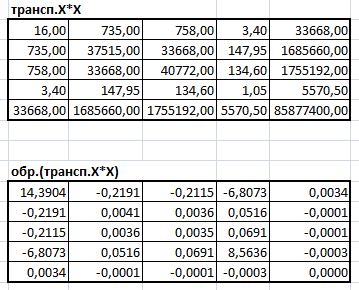Транспонированная матрица ХНайдемРисунок 12. 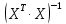Произведение транспонированной матрицы Х на матрицу ХНайдем Рисунок 13. 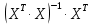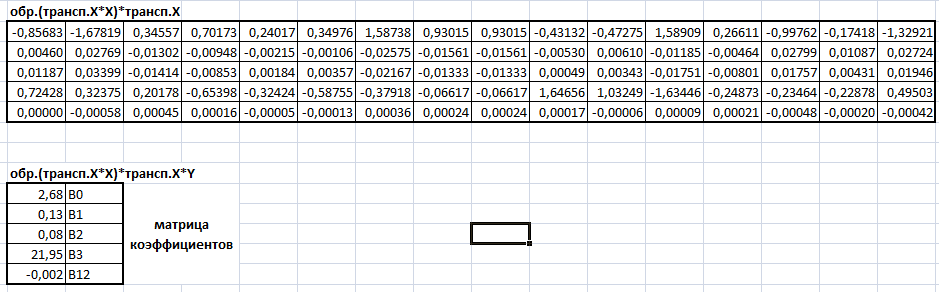Обратная матрица матрице произведенияНайдем Рисунок 14. 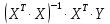Произведение обратной матрицы на транспонированную матрицу ХНайдем Рисунок 15. 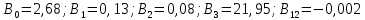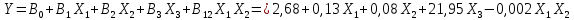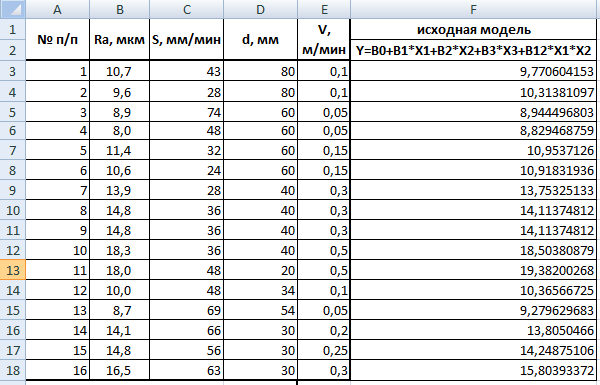Итоговая матрица коэффициентов ВПолучили Получаем модельВычислим значения этих функций Рисунок 16 – Вычисление значений Проверку адекватности полученной модели произведем путем сравнения двух дисперсий, одна из которых характеризует влияние на Y случайных факторов, а вторая, дисперсия адекватности , оценивает разброс опытных значений Y относительно линии регрессии.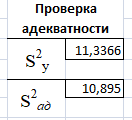Рисунок 17. Вычисление дисперсийПолучаем меньше , т. е. постулированная модель статистически значимо описывает процесс и может быть признана адекватной.