Файл: Справочник для опытных и как пособие для начинающих программистов. Компактдиск содержит исходные коды примеров из книги.doc
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 11.01.2024
Просмотров: 949
Скачиваний: 1
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
SharePoint Designer, MS Front Page и другими программами. При этом отступы и разные цвета позволяют выразительно увидеть структуру данного файла. XML-файл можно открыть табличным редактором MS Excel, и при этом он может отобразиться в виде таблицы. На рис. 7.7 приведен образец представления XML-файла в MS Word.
При использовании нами XML-файлов для данной задачи программирования простейшего табличного редактора совсем необязательно вникать в его структуру, тем более что при выборе имени файла для сохранения совершенно необязательно Устанавливать расширение файла xml, файл с любым расширением будет читаться Методом ReadXml, как XML-файл.
Программист может иметь доступ к полям таблицы. Например, доступ к левой верхней ячейке (полю) таблицы можно получить,, используя свойство объекта класса DataTable: Таблица.Rows.Item(0).Item(0). Однако запись этого поля, например, в последовательный файл будет некорректной даже при использовании дополнительной переменной из-за того, что технология ADO.NET предусматривает кэширование данных. Таким образом, чтение и запись данных для подобных лиц следует организовывать только через методы объекта DataSet.
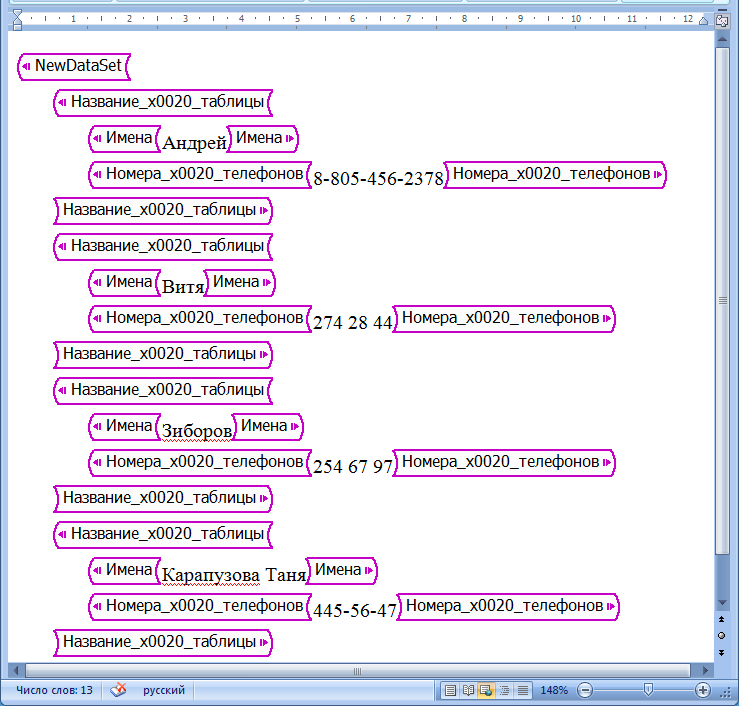
Рис. 7.7. Образец представления XML-файла в MS Word
Замечу, что данная программа может также являться инструментом для создания XML-файлов. Убедиться в работоспособности программы можно, открыв решение ТаблВвод-sln в папке ТаблВвод.
Пример 49. Решение системы линейных уравнений. Ввод коэффициентов через DataGridView
В инженерном деле, в экономических, научных расчетах часто встречается задача по решению системы линейных алгебраических уравнений (СЛАУ). Между тем, решение данной задачи последнее время редко приводится в книгах по языкам программирования. Данная программа приглашает пользователя ввести в текстовое поле количество неизвестных (т. е. размерность системы). Если пользователь справился с этим заданием, то это текстовое поле становится недоступным и появляется элемент управления сетка данных
DataGridView, куда пользователь имеет возможность ввести коэффициенты линейных уравнений и свободные члены. При целчке на кнопке Решить программа проверяет корректность введенных данных (не должно быть нечисловых символов, количество строк в матрице коэффициентов должно быть равно количеству неизвестных). Далее происходит непосредственное решение введенной системы методом Гаусса и вывод результатов вычислений с помощью MessageBox.
Таким образом, пользовательский интерфейс будет состоять (см. рис. 7.8) из формы, метки Label, текстового поля TextBox, элемента управления DataGridView и кнопки Button. В листинге 7.7 приведен программный код решения задачи.
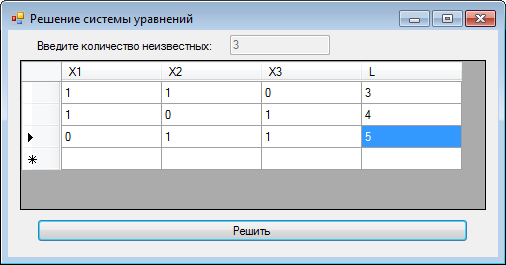
Рис. 7.8. Фрагмент табличного ввода данных
Листинг 7.7. Решение системы линейных уравнений
// Программа для решения системы линейных уравнений. Ввод коэффициентов
// предусмотрен через DataGridView
using System;
using System.Data;
using System.Windows.Forms;
// Другие директивы using удалены, поскольку они не используются в данной программе
namespace ГayccGrid
{
Public partial class Form1 : Form
{
int n; // - размерность СЛАУ
DataTable dt = new DataTable();
public Form1()
{
InitializeComponent();
base.Text = "Решение системы уравнений";
// Чтобы при старте программы фокус находился в текстовом поле:
textBox1.Tablndex = 0;
dataGridView1.Visible = false; // сетку данных пока не видно
ргlabel1.Text = "Ведите количество неизвестных:";
button1.Text = "Ввести"; // первоначальная надпись на кнопке
}
private void button1_Click(object sender, EventArgs e)
{
double[,] A = new double[n, n]; // - матрица коэффициентов
double[] L = new double[n]; // - вектор свободных членов
int i, j; bool Число_ли = false;
string tmp; // - временная рабочая переменная
if (button1.Text == "Ввести")
{
for (; ; )
{ // Бесконечный цикл, пока пользователь не введет именно число:
Число_ли = int.TryParse(textBox1.Text,
System.Globalization.NumberStyles.Integer,
System.Globalization.NumberFormatlnfo.Currentlnfо, out n) ;
if (Число_ли == false) return;
button1.Text = "Решить";
textBox1.Enabled = false; // теперь текстовое поле недоступно
dataGridView1.Visible = true; // сетку данных теперь уже видно
dataGridView1.DataSource = dt;
// Создаем "шапку" таблицы
for (i = 1; i <= n; i++)
{
tmp = "X" + Convert.ToString(i);
dt.Columns.Add(new DataColumn(tmp));
}
// Колонка правой части системы:
dt.Columns.Add(new DataColumn(" L"));
return;
}
}
else // buttonl.Text == "Решить")
{ // Нажали кнопку "Решить"
// dt.Rows.Count - количество рядов
if (dt.Rows.Count != n)
{
MessageBox.Show("Количество строк не равно количеству колонок");
return;
}
// Заполнение матрицы коэффициентов системы A[j, i]
for (j = 0; j <= n - 1; j++)
{
for (i = 0; i <= n - 1; i++)
{
A[j, i] = ВернутьЧисло(j, i, ref Число_ли);
if (Число_ли == false) return;
}
// Правая часть системы B(j, 0)
L[j] = ВернутьЧисло(j, i, ref Число_ли);
if (Число_ли == false) return;
} // j
}
gauss(n, A, ref L); // Решение системы A*x = L методом Гаусса
// L - вектор свободных членов системы, сюда же возвращается
// решение х
string s = "Неизвестные равны:\n";
for (j = 1; j <= n; j++)
{
tmp = L[j - 1].ToString();
s = s + "X" + j.ToString() + " = " + tmp + ";\n";
}
MessageBox.Show(s);
}
private void gauss(int n, double[,] A, ref double[] LL)
{ // n - размер матрицы
//A - матрица коэффициентов Линейных уравнений
// LL - правая часть, сюда возвращаются значения неизвестных
int i, j, 1=0;
Double c1, c2, c3;
for (i = 0; i <= n - 1; i++) // цикл по элементам строки
{
c1 = 0;
for (j = i; j <= n - 1; j++)
{
c2 = A[j, i];
if (Math.Abs(c2) > Math.Abs(c1))
{
1 = j; c1 = c2;
}
}
for (j = i; j <= n - 1; j++)
{
сЗ = A[1, j] / c1;
A[l, j] = A[i, j]; A[i, j] = c3;
} // j
c3 = LL[1] / c1; LL[1] = LL[i]; LL[i] = c3;
for (j = 0; j <= n - 1; j++)
{
if (j == i) continue;
for (1 = i + 1; 1 <= n - 1; 1++)
{
A[j, 1] = A[j, 1] - A[i, 1] * A[j, i] ;
} // 1
LL[j] = LL[j] - LL [i] * A[j, i] ;
} // j
} // i
}
private double ВернутьЧисло(int j, int i, ref bool Число_ли)
{ // j - номер строки, i - номер столбца
double rab; // - рабочая переменная
string tmp = dt .Rows [j][i].ToString ();
Число_ли = Double.TryParse(tmp, Sys tern.Globalization.NumberStyles.Number, System.Globalization.NumberFormatlnfo.Currentlnfo, out rab);
if (Число_ли == false)
{
tmp = String.Format("Номер строки {0}, номер столбца " +
"{1},\п в данном поле - не число", j + 1, i + 1)■ Mes sageBox.Show(tmp);
}
return rab;
}
}
}
Как видно их программного кода, при начальной загрузке программы польза ватель не видит (visible = false) сетку данных, а первоначальная надпись нa кнопке — "Ввести". При щелчке на кнопке, если пользователь корректно ввел количество неизвестных, меняем надпись на кнопке (она теперь будет "Решить"), по количеству неизвестных подготавливаем "шапку" таблицы и размерность сетки данных, куда пользователь будет вводить коэффициенты линейных уравнений и свободные члены.
После ввода коэффициентов и щелчка на кнопке Решить происходит проверка количества введенных рядов коэффициентов и проверка на нечисловые символы. После этого вызывается процедура решения СЛАУ методом Гаусса gauss, т. е. методом последовательного исключения
неизвестных. В основе процедуры gauss — цикл for по элементам строки матрицы системы. В этот внешний цикл вложены три внутренних цикла по строкам матрицы. После вызова процедуры gauss формируется строковая переменная s для вывода значений неизвестных, которая выводится посредством диалогового окна MessageBox (рис. 7.9).
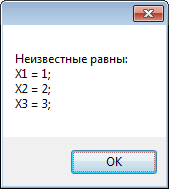
Рис. 7.9. Вывод неизвестных значений в диалоговое окно
Данная программа не предусматривает проверку на вырожденность СЛАУ, однако в этом случае в качестве значений неизвестных пользователь получает либо "бесконечность", либо константу NaN, значение которой является результатом деления на ноль. Программа не предусматривает ограничение сверху на размерность решаемой системы и должна работать при любой разумной размерности. Работа программы должна быть ограничена лишь размером оперативной памяти. Однако автор не тестировал эту программу на решение систем большой размерности. Если количество неизвестных равно одному, то программа также нормально функционирует.
Убедиться в работоспособности программы можно, открыв решение ГаусcGrid.sln в папке ГayccGrid.
ГЛАВА 8. Элемент управления WebBrowser
Пример 50. Отображение HTML-таблиц
В этом примере воспользуемся элементом управления WebBrowser для отображения таблицы, записанной на языке HTML с помощью элементарных тегов: <tr>, задающего строку в таблице, и <td>, задающего ячейку в таблице. Понятно, что, сформировав такой HTML-файл, содержащий таблицу, подлежащую выводу на экран, можно вывести этот файл в поле элемента управления WebBrowser с помощью метода Navigate объекта.
Покажем, как, задав на языке HTML какую-нибудь таблицу в строковой переменной, можно вывести эту таблицу в поле элемента управления WebBrowser, при этом не записывая на винчестер HTML-файл. Для этой цели воспользуемся простейшей таблицей из примера о формировании таблицы.
Приступим к программированию поставленной задачи. Запустим Visual Studio 2010 и выберем новый проект. Панель элементов Toolbox содержит в себе элемент WebBrowser, который перетаскиваем в форму. Текст программы приведен в листинге 8.1.
Листинг 8.1. Отображение таблиц с помощью элемента управления WebBrowser
//В программе для отображения таблицы используется элемент управления
// WebBrowser. Таблица записана на языке HTML с помощью элементарных
// тегов
При использовании нами XML-файлов для данной задачи программирования простейшего табличного редактора совсем необязательно вникать в его структуру, тем более что при выборе имени файла для сохранения совершенно необязательно Устанавливать расширение файла xml, файл с любым расширением будет читаться Методом ReadXml, как XML-файл.
Программист может иметь доступ к полям таблицы. Например, доступ к левой верхней ячейке (полю) таблицы можно получить,, используя свойство объекта класса DataTable: Таблица.Rows.Item(0).Item(0). Однако запись этого поля, например, в последовательный файл будет некорректной даже при использовании дополнительной переменной из-за того, что технология ADO.NET предусматривает кэширование данных. Таким образом, чтение и запись данных для подобных лиц следует организовывать только через методы объекта DataSet.

Рис. 7.7. Образец представления XML-файла в MS Word
Замечу, что данная программа может также являться инструментом для создания XML-файлов. Убедиться в работоспособности программы можно, открыв решение ТаблВвод-sln в папке ТаблВвод.
Пример 49. Решение системы линейных уравнений. Ввод коэффициентов через DataGridView
В инженерном деле, в экономических, научных расчетах часто встречается задача по решению системы линейных алгебраических уравнений (СЛАУ). Между тем, решение данной задачи последнее время редко приводится в книгах по языкам программирования. Данная программа приглашает пользователя ввести в текстовое поле количество неизвестных (т. е. размерность системы). Если пользователь справился с этим заданием, то это текстовое поле становится недоступным и появляется элемент управления сетка данных
DataGridView, куда пользователь имеет возможность ввести коэффициенты линейных уравнений и свободные члены. При целчке на кнопке Решить программа проверяет корректность введенных данных (не должно быть нечисловых символов, количество строк в матрице коэффициентов должно быть равно количеству неизвестных). Далее происходит непосредственное решение введенной системы методом Гаусса и вывод результатов вычислений с помощью MessageBox.
Таким образом, пользовательский интерфейс будет состоять (см. рис. 7.8) из формы, метки Label, текстового поля TextBox, элемента управления DataGridView и кнопки Button. В листинге 7.7 приведен программный код решения задачи.

Рис. 7.8. Фрагмент табличного ввода данных
Листинг 7.7. Решение системы линейных уравнений
// Программа для решения системы линейных уравнений. Ввод коэффициентов
// предусмотрен через DataGridView
using System;
using System.Data;
using System.Windows.Forms;
// Другие директивы using удалены, поскольку они не используются в данной программе
namespace ГayccGrid
{
Public partial class Form1 : Form
{
int n; // - размерность СЛАУ
DataTable dt = new DataTable();
public Form1()
{
InitializeComponent();
base.Text = "Решение системы уравнений";
// Чтобы при старте программы фокус находился в текстовом поле:
textBox1.Tablndex = 0;
dataGridView1.Visible = false; // сетку данных пока не видно
ргlabel1.Text = "Ведите количество неизвестных:";
button1.Text = "Ввести"; // первоначальная надпись на кнопке
}
private void button1_Click(object sender, EventArgs e)
{
double[,] A = new double[n, n]; // - матрица коэффициентов
double[] L = new double[n]; // - вектор свободных членов
int i, j; bool Число_ли = false;
string tmp; // - временная рабочая переменная
if (button1.Text == "Ввести")
{
for (; ; )
{ // Бесконечный цикл, пока пользователь не введет именно число:
Число_ли = int.TryParse(textBox1.Text,
System.Globalization.NumberStyles.Integer,
System.Globalization.NumberFormatlnfo.Currentlnfо, out n) ;
if (Число_ли == false) return;
button1.Text = "Решить";
textBox1.Enabled = false; // теперь текстовое поле недоступно
dataGridView1.Visible = true; // сетку данных теперь уже видно
dataGridView1.DataSource = dt;
// Создаем "шапку" таблицы
for (i = 1; i <= n; i++)
{
tmp = "X" + Convert.ToString(i);
dt.Columns.Add(new DataColumn(tmp));
}
// Колонка правой части системы:
dt.Columns.Add(new DataColumn(" L"));
return;
}
}
else // buttonl.Text == "Решить")
{ // Нажали кнопку "Решить"
// dt.Rows.Count - количество рядов
if (dt.Rows.Count != n)
{
MessageBox.Show("Количество строк не равно количеству колонок");
return;
}
// Заполнение матрицы коэффициентов системы A[j, i]
for (j = 0; j <= n - 1; j++)
{
for (i = 0; i <= n - 1; i++)
{
A[j, i] = ВернутьЧисло(j, i, ref Число_ли);
if (Число_ли == false) return;
}
// Правая часть системы B(j, 0)
L[j] = ВернутьЧисло(j, i, ref Число_ли);
if (Число_ли == false) return;
} // j
}
gauss(n, A, ref L); // Решение системы A*x = L методом Гаусса
// L - вектор свободных членов системы, сюда же возвращается
// решение х
string s = "Неизвестные равны:\n";
for (j = 1; j <= n; j++)
{
tmp = L[j - 1].ToString();
s = s + "X" + j.ToString() + " = " + tmp + ";\n";
}
MessageBox.Show(s);
}
private void gauss(int n, double[,] A, ref double[] LL)
{ // n - размер матрицы
//A - матрица коэффициентов Линейных уравнений
// LL - правая часть, сюда возвращаются значения неизвестных
int i, j, 1=0;
Double c1, c2, c3;
for (i = 0; i <= n - 1; i++) // цикл по элементам строки
{
c1 = 0;
for (j = i; j <= n - 1; j++)
{
c2 = A[j, i];
if (Math.Abs(c2) > Math.Abs(c1))
{
1 = j; c1 = c2;
}
}
for (j = i; j <= n - 1; j++)
{
сЗ = A[1, j] / c1;
A[l, j] = A[i, j]; A[i, j] = c3;
} // j
c3 = LL[1] / c1; LL[1] = LL[i]; LL[i] = c3;
for (j = 0; j <= n - 1; j++)
{
if (j == i) continue;
for (1 = i + 1; 1 <= n - 1; 1++)
{
A[j, 1] = A[j, 1] - A[i, 1] * A[j, i] ;
} // 1
LL[j] = LL[j] - LL [i] * A[j, i] ;
} // j
} // i
}
private double ВернутьЧисло(int j, int i, ref bool Число_ли)
{ // j - номер строки, i - номер столбца
double rab; // - рабочая переменная
string tmp = dt .Rows [j][i].ToString ();
Число_ли = Double.TryParse(tmp, Sys tern.Globalization.NumberStyles.Number, System.Globalization.NumberFormatlnfo.Currentlnfo, out rab);
if (Число_ли == false)
{
tmp = String.Format("Номер строки {0}, номер столбца " +
"{1},\п в данном поле - не число", j + 1, i + 1)■ Mes sageBox.Show(tmp);
}
return rab;
}
}
}
Как видно их программного кода, при начальной загрузке программы польза ватель не видит (visible = false) сетку данных, а первоначальная надпись нa кнопке — "Ввести". При щелчке на кнопке, если пользователь корректно ввел количество неизвестных, меняем надпись на кнопке (она теперь будет "Решить"), по количеству неизвестных подготавливаем "шапку" таблицы и размерность сетки данных, куда пользователь будет вводить коэффициенты линейных уравнений и свободные члены.
После ввода коэффициентов и щелчка на кнопке Решить происходит проверка количества введенных рядов коэффициентов и проверка на нечисловые символы. После этого вызывается процедура решения СЛАУ методом Гаусса gauss, т. е. методом последовательного исключения
неизвестных. В основе процедуры gauss — цикл for по элементам строки матрицы системы. В этот внешний цикл вложены три внутренних цикла по строкам матрицы. После вызова процедуры gauss формируется строковая переменная s для вывода значений неизвестных, которая выводится посредством диалогового окна MessageBox (рис. 7.9).

Рис. 7.9. Вывод неизвестных значений в диалоговое окно
Данная программа не предусматривает проверку на вырожденность СЛАУ, однако в этом случае в качестве значений неизвестных пользователь получает либо "бесконечность", либо константу NaN, значение которой является результатом деления на ноль. Программа не предусматривает ограничение сверху на размерность решаемой системы и должна работать при любой разумной размерности. Работа программы должна быть ограничена лишь размером оперативной памяти. Однако автор не тестировал эту программу на решение систем большой размерности. Если количество неизвестных равно одному, то программа также нормально функционирует.
Убедиться в работоспособности программы можно, открыв решение ГаусcGrid.sln в папке ГayccGrid.
ГЛАВА 8. Элемент управления WebBrowser
Пример 50. Отображение HTML-таблиц
В этом примере воспользуемся элементом управления WebBrowser для отображения таблицы, записанной на языке HTML с помощью элементарных тегов: <tr>, задающего строку в таблице, и <td>, задающего ячейку в таблице. Понятно, что, сформировав такой HTML-файл, содержащий таблицу, подлежащую выводу на экран, можно вывести этот файл в поле элемента управления WebBrowser с помощью метода Navigate объекта.
Покажем, как, задав на языке HTML какую-нибудь таблицу в строковой переменной, можно вывести эту таблицу в поле элемента управления WebBrowser, при этом не записывая на винчестер HTML-файл. Для этой цели воспользуемся простейшей таблицей из примера о формировании таблицы.
Приступим к программированию поставленной задачи. Запустим Visual Studio 2010 и выберем новый проект. Панель элементов Toolbox содержит в себе элемент WebBrowser, который перетаскиваем в форму. Текст программы приведен в листинге 8.1.
Листинг 8.1. Отображение таблиц с помощью элемента управления WebBrowser
//В программе для отображения таблицы используется элемент управления
// WebBrowser. Таблица записана на языке HTML с помощью элементарных
// тегов