Файл: Построение приближенных разверток развертывающихся поверхностей.doc
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 11.01.2024
Просмотров: 56
Скачиваний: 1
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
Построение приближенных разверток развертывающихся поверхностей
Мы уже указывали, что к развертывающимся поверхностям относятся только торсы (поверхности с ребром возврата, коническая и цилиндрическая поверхности).
Развертка любой развертывающейся поверхности (кроме гранных) является приближенной. Это объясняется тем, что при развертке поверхности последнюю аппроксимируют поверхностями вписанных или описанных многогранников, имеющих грани в форме прямоугольников или треугольников. Поэтому при графическом выполнении развертки поверхности всегда приходится производить разгибание или спрямление кривых линий, принадлежащих поверхности, что неизбежно приводит к потере точности.
Рассмотрим способы построения приближенных разверток поверхностей: цилиндрической, конической и с ребром возврата.
А. Построение развертки цилиндрической поверхности.
Для построения развертки цилиндрической поверхности используются те же способы нормального сечения и раскатки, которые применяются при развертывании боковой поверхности призмы.
В
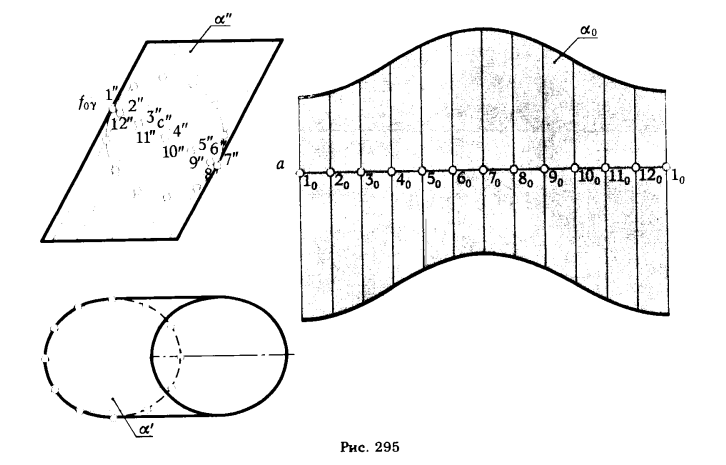обоих случаях цилиндрическую поверхность заменяют призматической поверхностью, вписанной (или описанной) в данную цилиндрическую. Затем задачу решают так же, как это было показано в примерах 1 и 2 предыдущего параграфа. На рис. 295 и 296 показано построение боковой поверхности цилиндра способом нормального сечения (рис. 295) и способом раскатки (рис. 296).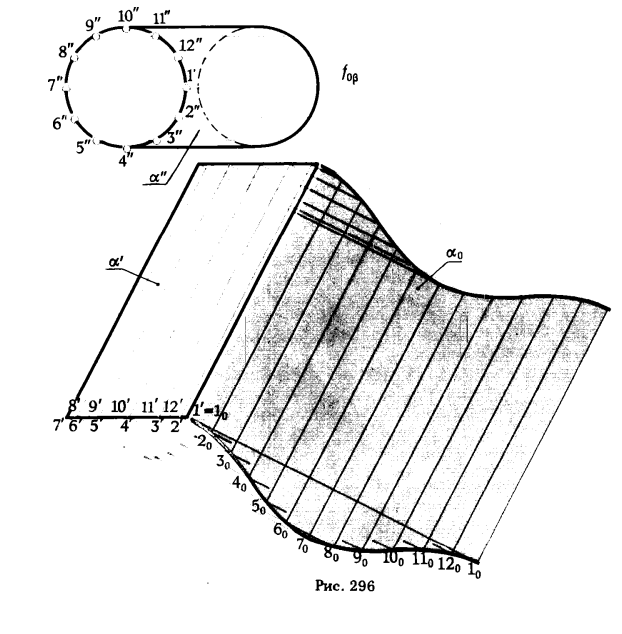
При построении развертки поверхности цилиндра вращения предпочтение следует отдать способу нормального сечения, так как в этом случае можно не прибегать к замене цилиндрической поверхности призматической.
Для того чтобы построить развертку поверхности прямого кругового цилиндра, выполняем следующие геометрические построения:
1. Рассекаем цилиндрическую поверхность α плоскостью γ, перпендикулярной к прямолинейной образующей цилиндрической поверхности.
2.Делим окружность с — линию сечения α ∩ γ на одинаковое число частей n.
3. Проводим в свободном месте чертежа прямую а и отмечаем на ней отрезок 1010 равный длине окружности сечения с.
4. Делим [1010] на такое же число одинаковых частей n, на которое была разделена окружность с.
5. Через точки деления 10, 20, 30,..., 120, 10 проводим прямые,перпендикулярные к прямой а , и откладываем на них от точек 10, 20,30,..., 120, 10 отрезки, равные длине соответствующих образующихнижней и верхней частей цилиндрической поверхности.
6. Соединив концы образующих плавной кривой, получим развертку цилиндрической поверхности.
На рис. 296 приведен пример построения развертки боковой поверхности эллиптического цилиндра способом раскатки. Необходимые геометрические построения выполняем в следующем порядке:
1. Делим окружность основания цилиндра на n равных частей (на рис. 296 n = 12).
2. Через точки деления проводим прямолинейные образующие цилиндрической поверхности — ребра призмы, которой мы заменяем цилиндрическую поверхность α.
3. Принимаем за плоскость развертки горизонтальную плоскость β, проходящую через ребро 1 призмы, тождественное 1-й образующей цилиндрической поверхности
Дальнейшие построения аналогичны выполненным на рис. 293 при построении развертки боковой поверхности призмы ABCDEF.
Б. Построение развертки конической поверхности.
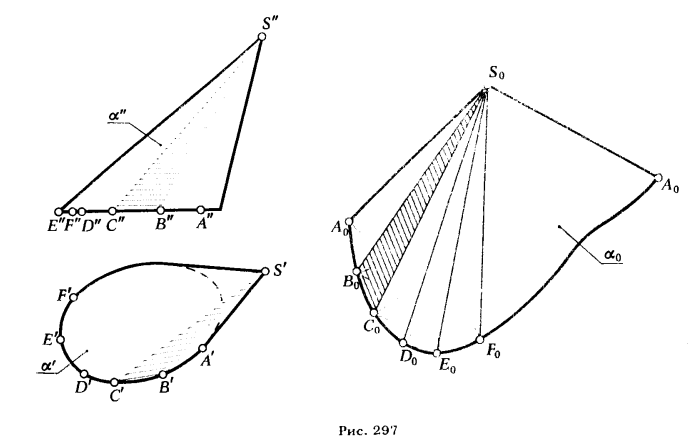
Задача на построение развертки конической поверхности решается так же, как в случае построения развертки боковой поверхности пирамиды — способом треугольников (см. рис. 294). Для этого коническая поверхность аппроксимируется вписанной в нее пирамидальной поверхностью.
На рис. 297 показана развертка поверхности пирамиды SABCDEF...,вписанной в заданную коническую поверхность α. Фигуру S0A0B0C0D0E0F0 ... A0 принимаем за приближенную развертку конической поверхности. Чем больше число граней у вписанной пирамиды, тем меньше будет разница между действительной и приближенной развертками конической поверхности.
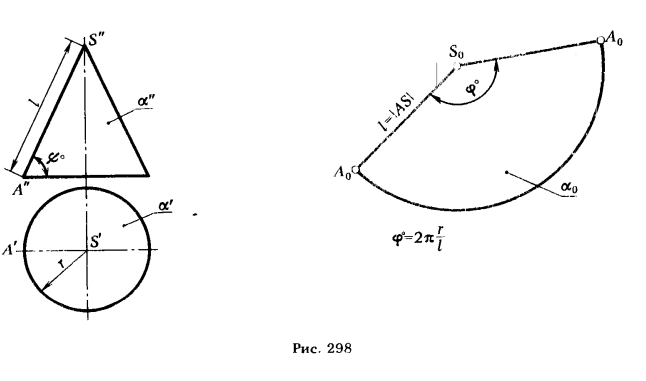
Если задана поверхность прямого кругового конуса (рис. 298), то развертка его боковой поверхности представляет круговой сектор, радиус которого равен длине образующей конической поверхности l = |SA|, а центральный угол
= 2πr/l, где r — радиус окружности основания конуса. Величина угла φ получается в радианах. На практике бывает целесообразно иметь его градусную величину. Это легко сделать, подставив в приведенное равенство значение величины l, выраженное через радиус основания конуса r и угол наклона образующей конической поверхности к плоскости π1 (∠ψ°). В этом случае l = r/cosψ°, тогда
= 2πrcosψ°/r - 360° cosψ°.На рис. 299 показано построение развертки поверхности прямого кругового усеченного конуса, вершина которого находится за пределами поля чертежа.
Решение этой задачи осуществляется следующим путем:
1) строим вспомогательный конус β, подобный данному конусу α, диаметр d основания конуса β следует выбирать так, чтобы отношение D/d (где D -- диаметр окружности основания конуса α) выражалось целым числом (на рис. 299 оно равно 2);
2) строим развертку боковой поверхности вспомогательного конуса β - S0A01020 ... 50A0;
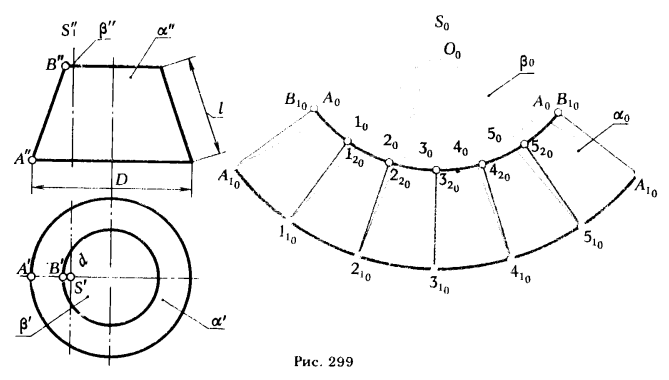
3) из произвольной точки О0, принадлежащей биссектрисе угла A0S0A0, проводим лучи [О0 А0), [О010), [О020), ..., [О0А0) и на них откладываем отрезки [О0А10] = k[O0A00, [О0110] = k[O010], [О0210] = k[О020],..., [О0 А10] = k[O0A0 ], где k = D/d = 2.
Для построения развертки поверхности α достаточно определить положение точки А10 и через нее провести дугу окружности радиусом, равным длине отрезка |О0A10] из центра в точке О0. Эта окружность пересечет лучи [О010), [О00), ... в точках 110, 20, ... Из точек А10, 110, 210, ... проводим прямые (A10B10 ), (110120), (210220), параллельные соответствующим прямым (A0S0), (10S0), (20S0), ..., и на них откладываем отрезки [А10 B10], [110,120], [210 220], ..., равные l — длине образующей АВ усеченного конуса α.
В. Построение развертки поверхности с ребром возврата.
Построение развертки поверхности с ребром возврата осуществляется путем аппроксимации ее отсеками конической поверхности с последующей заменой их плоскими треугольниками. В качестве иллюстрации решения такой задачи обратимся к следующему примеру:
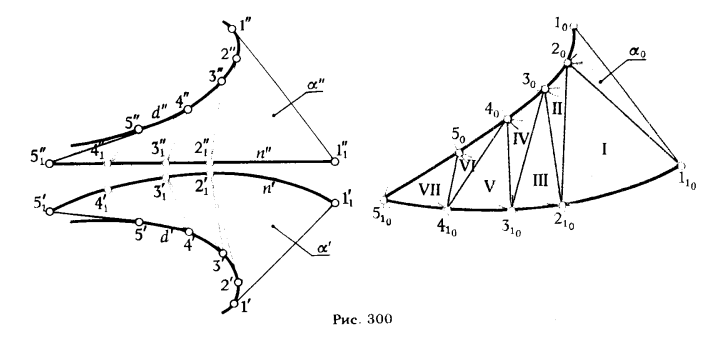
пусть на эпюре Монжа заданы проекции поверхности с ребром возврата α; построить ее развертку (рис. 300).
На ребре возврата d отмечаем ряд точек 1, 2, 3, 4, 5 и через их проекции проводим касательные к проекциям d' и d" — [ 111 ], [ 221 ] , [ 331 ], [ 441 ], [ 551 ] . В отсеках поверхностей, ограниченных этими касательными, проводим диагонали 211 , 321 , ..., которые делят каждый из криволинейных четырехугольников на два "треугольника".
Если расстояния между точками 1 и 2, 2 и З, З и 4, 4 и 5 будут достаточно малыми, то стороны "треугольников", противолежащие вершинам 11, 21, 31, 41 (и 110, 210, 310, 410), можно считать прямолинейными.
Для построения развертки многогранной поверхности, аппроксимирующей заданную поверхность α, определяем длины сторон этих треугольников. По трем сторонам строим треугольники, начиная с Δ1020110, к которому пристраиваем остальные в последовательности, указанной на рис. 300 римскими цифрами. Фигура 1020304050 510410310210110 — приближенная развертка поверхности α.
