Добавлен: 11.01.2024
Просмотров: 42
Скачиваний: 1
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
Задача 2
Решение
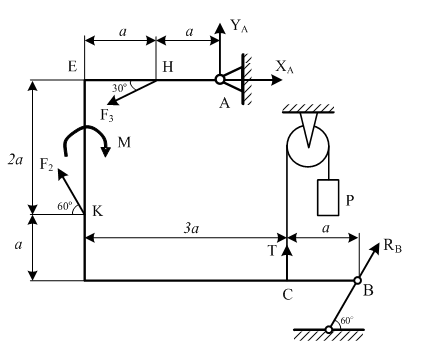
Рассмотрим равновесие жесткой рамы. На раму действуют силы: силы
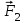 и
и 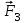 , пара сил с моментом М, натяжение троса
, пара сил с моментом М, натяжение троса 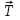 (
(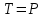 ) и реакции связей
) и реакции связей 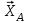 ,
, 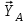 ,
, 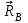 .
.Неизвестны реакции связей
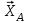 ,
, 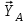 ,
, 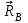 .
.Для полученной плоской системы сил составим три уравнения равновесия:
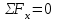 ,
, 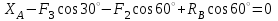 (1)
(1)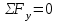 ,
, 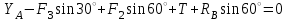 (2)
(2)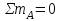 ,
, 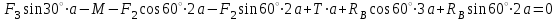 (3)
(3)Из уравнения (3):
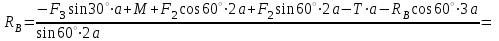
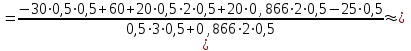 41,66 кН
41,66 кНИз уравнения (2):
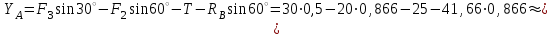 -63,4 кН
-63,4 кНИз уравнения (1):
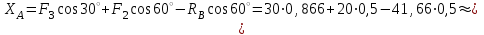 15,15 кН
15,15 кНРеакции, полученные со знаком «минус», в действительности имеют направление противоположное принятому на рисунке.
Проверка:
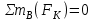
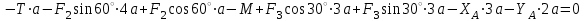
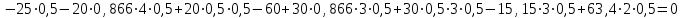
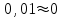
Ответ: ХА = 15,15 кН, YA = -63,4 кH, RB = 41,66 кH
Задача 3
Решение
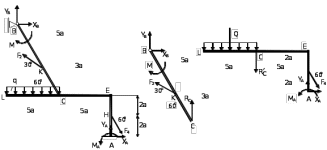
Для определения реакций расчленим систему и рассмотрим вначале равновесие стержня ВС.
На стержень действуют сила
 , пара сил с моментом М, реакция
, пара сил с моментом М, реакция 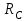 и составляющие
и составляющие 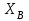 ,
, 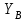 реакции опоры В.
реакции опоры В.Для полученной плоской системы сил составляем уравнения равновесия:
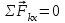 ;
; 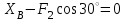 (1)
(1)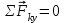 ;
; 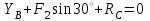 (2)
(2)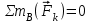 ;
; 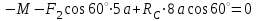 (3)
(3)Из (3):
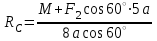 =
=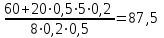 (кН)
(кН)Из (2):
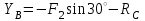 =
=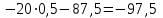 (кН)
(кН) Из (1):
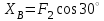 =
=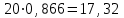 (кН)
(кН)Теперь рассмотрим равновесие угольника АЕL. На него действует сила
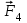 , равномерно распределенная нагрузка, которую заменим силой
, равномерно распределенная нагрузка, которую заменим силой 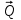 , приложенной в середине участка
, приложенной в середине участка 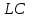 (
(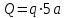 =20 кН), сила давления стержня ВС
=20 кН), сила давления стержня ВС 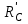 (направлена противоположно
(направлена противоположно 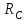 и численно
и численно 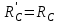 ) и реакция жесткой заделки А (
) и реакция жесткой заделки А ( ,
,  ,
, 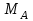 ).
).Для этой плоской системы сил тоже составим уравнения равновесия:
 ;
; 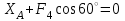 (4)
(4) ;
; 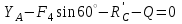 (5)
(5)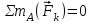 ;
; 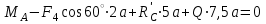 (6)
(6)Из (4):
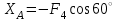 =
=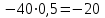 (кН)
(кН) Из (5):
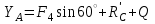 =
=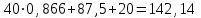 (кН)
(кН)Из (6):
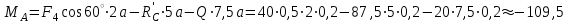 (кНм)
(кНм) Реакции, полученные со знаком «минус» в действительности имеют направление противоположное принятому на рисунке.
Проверка (для всей конструкции):
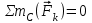
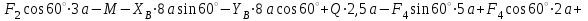
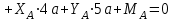
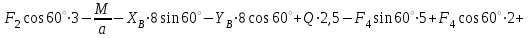
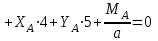
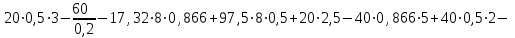
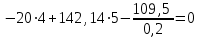

Ответ:
| МА | ХА | YA | RС | ХВ | YВ |
| кНм | кН | ||||
| –109,5 | –20 | 142,14 | 87,5 | 17,32 | –97,5 |
Задача 4
Решение
С
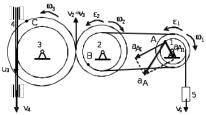 корости точек, лежащих на ободах колес радиуса
корости точек, лежащих на ободах колес радиуса 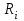 , обозначим через
, обозначим через 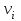 , а точек, лежащих на ободах колес радиуса
, а точек, лежащих на ободах колес радиуса 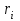
, через
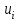 .
.Угловые скорости всех колес.
Колеса 3 и 2 находятся в зацеплении, следовательно,
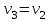 , то есть
, то есть 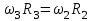 и отсюда
и отсюда 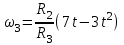 .
. При t1=2 c
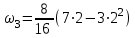 =1 (1/с).
=1 (1/с).Скорость
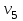
Т.к. колеса 2 и 1 связаны ременной передачей, то
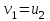 или
или 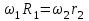 и
и 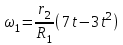 .
.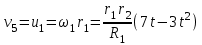 .
. При t1=2 c
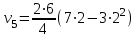 =6 (см/с)
=6 (см/с)Угловое ускорение
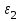 .
. Так как
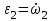 , то
, то 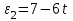 =
=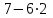 = –5 (1/с2).
= –5 (1/с2).Ускорение
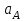 .
. Для т.А
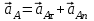 , где
, где 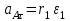 ,
, 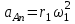 .
. Угловое ускорение
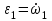 =
=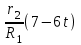 =
=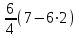 = –7,5 (1/с2).
= –7,5 (1/с2). Таким образом при t1=2 c
касательная составляющая
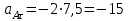 (см/с2),
(см/с2), нормальная составляющая
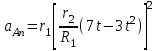 =
=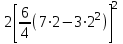 = 18 (см/с2),
= 18 (см/с2),полное ускорение
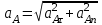 =
=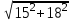
= 23,4 (см/с2).
Ускорение
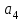 .
. Т.к. рейка 4 совершает поступательное движение, то
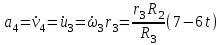 .
. Тогда
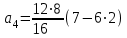 = –30 (см/с2).
= –30 (см/с2).Ответ:
| v5 | 3 | 2 | aА | a4 |
| см/с | 1/с | 1/с2 | см/с2 | |
| 6 | 1 | –5 | 23,4 | –30 |
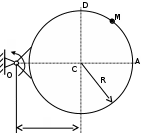 Задача 5
Задача 5Решение
Рассматриваем движение т.М как сложное, считая ее движение по окружности относительным, а вращение пластины – переносным. Тогда абсолютная скорость и абсолютное ускорение точки найдутся по формулам:
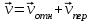 ,
,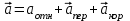 или в развернутом виде
или в развернутом виде 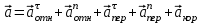 .
.Положение т.М:
При t=1с
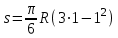 =
=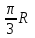 (см) – т.М находится в области положительных значений выше т.А.
(см) – т.М находится в области положительных значений выше т.А.Тогда АСМ=
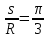 = 60о, а DСМ=30о.
= 60о, а DСМ=30о. Расстояние от оси вращения О до т.М :
 =104 (см).
=104 (см). Относительное движение.
Относительная скорость
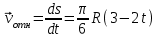 .
. При
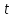 = 1 с
= 1 с 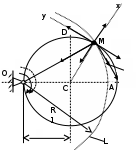
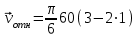 = 31,4 (см/с) – вектор направлен в сторону положительных значений
= 31,4 (см/с) – вектор направлен в сторону положительных значений 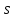 .
.Модуль относительной скорости