Добавлен: 11.01.2024
Просмотров: 43
Скачиваний: 1
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
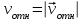 =31,4 см/с.
=31,4 см/с.Модуль относительного касательного ускорения
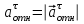 , где
, где 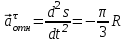 .
. При
 =1с
=1с 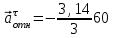 = –62,8 (см/с2).
= –62,8 (см/с2). Значит
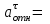 62,8 (см/с2).
62,8 (см/с2).Вектор
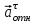 направлен в сторону отрицательных значений
направлен в сторону отрицательных значений  . Знаки
. Знаки 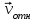 и
и 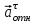 разные, следовательно, относительное движение т.М замедленное.
разные, следовательно, относительное движение т.М замедленное.Относительное нормальное ускорение
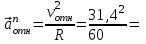 16,4 (см/с2).
16,4 (см/с2).Переносное движение.
Модуль переносной скорости
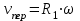 ,
, где R1 – радиус окружности L, описываемой той точкой тела, с которой совпадает в данный момент т.М
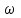 – модуль угловой скорости тела:
– модуль угловой скорости тела: 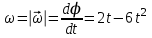 .
.При
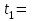 1 с
1 с 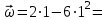 –4 1/с;
–4 1/с; 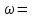 4 рад/с.
4 рад/с.Модуль переносной скорости:
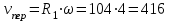 (см/с). Вектор
(см/с). Вектор 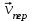 направлен по касательной к окружности L в сторону вращения тела.
направлен по касательной к окружности L в сторону вращения тела.Модуль переносного вращательного ускорения
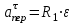 , где
, где 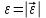 - модуль углового ускорения тела Д:
- модуль углового ускорения тела Д: 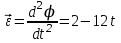
При
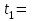 1 с
1 с 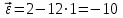 (1/с2); то есть переносное вращательное движение –ускоренное, так как знаки
(1/с2); то есть переносное вращательное движение –ускоренное, так как знаки
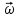 и
и 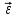 одинаковы.
одинаковы. Значит
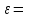 10 1/с2 и
10 1/с2 и 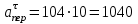 (см/с2).
(см/с2).Вектор
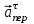 направлен в по
направлен в по  .
.Модуль переносного центростремительного ускорения
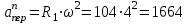 (см/с2).
(см/с2). Вектор
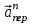 направлен от т .М к оси вращения.
направлен от т .М к оси вращения.Кориолисово ускорение
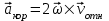 .
.Модуль кориолисова ускорения
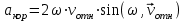 , где
, где 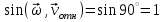 .
. Так как
 4 рад/с, а
4 рад/с, а 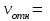 31,4см/с, то
31,4см/с, то 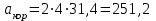 (см/с2).
(см/с2).Вектор
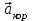 направлен в соответствии с правилом векторного произведения.
направлен в соответствии с правилом векторного произведения.Абсолютная скорость.
Абсолютную скорость т.М найдем как геометрическую сумму относительной и переносной скоростей. Векторы
 и
и  расположены под углом 150о (см. рисунок) друг к другу.
расположены под углом 150о (см. рисунок) друг к другу.Модуль абсолютной скорости
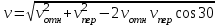
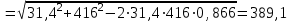 (см/с)
(см/с)Абсолютное ускорение.
Все векторы лежат в плоскости чертежа. Модуль абсолютного ускорения находим методом проекций:
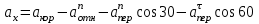 =
=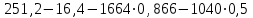 = –1726,2 (см/с2)
= –1726,2 (см/с2)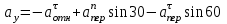 =
=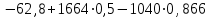 = –131,4(см/с2)
= –131,4(см/с2)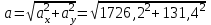 =1731 (см/с2)
=1731 (см/с2)