Файл: Урок 4 в теме Комплексные числа Базовый учебник.docx

Скачать файл
Заказать решение

ВУЗ: Не указан

Категория: Не указан

Дисциплина: Не указана

Добавлен: 11.01.2024

Просмотров: 29

Скачиваний: 2

ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.

ТЕХНОЛОГИЧЕСКАЯ КАРТА УРОКА

  1. Ф.И.О: Соболева Инна Ивановна

  2. Место работы: МБОУ «Хохольский лицей»

  3. Должность: учитель

  4. Предмет: математика

  5. Класс: 10

  6. Тема и номер урока в теме: Тригонометрическая запись комплексного числа. Урок №4 в теме «Комплексные числа»

  7. Базовый учебник:

  1. Алгебра и начала математического анализа 10 класс. Учебник для учащихся общеобразовательных учреждений (профильный уровень)/ А. Г. Мордкович, П.В.Семенов - М.: Мнемозина 2009 г.;

  2. Алгебра и начала математического анализа 10 класс. Задачник для учащихся общеобразовательных учреждений (профильный уровень)/ А. Г. Мордкович, П.В.Семенов - М.: Мнемозина 2009 г..

  1. Цель урока: формирование способности учащихся к новому способу действия, расширение понятийной базы за счет введения понятия тригонометрическая запись комплексного числа; изучение системы аналитических вычислений wxMaxima.

  2. Формируемые предметные результаты: умеют представлять в тригонометрической форме комплексное число; формулируют алгоритм записи числа в тригонометрической форме.

  3. Формируемые метапредметные результаты:

- личностные универсальные учебные действия: проявляют дисциплинированность, трудолюбие и упорство в достижении поставленных целей; развитие познавательных интересов, учебных мотивов; оценивание усваиваемого содержания, исходя из социальных и личностных ценностей, владеют навыками совместной деятельности.

- регулятивные универсальные учебные действия: умеютпоставить учебную задачу, определить последовательности промежуточных целей с учётом конечного результата, прогнозировать, контролировать и корректировать знания; осознают качество и уровень усвоения; проявляют способность к мобилизации сил и энергии.

- познавательные универсальные учебные действия: изучают система аналитических вычислений wxMaxima, как новый инструмента для решения математических задач; установление причинно-следственные связи; строят логической цепи рассуждений; выдвигают гипотезы и их обосновывают; самостоятельно создают способы решения проблем творческого и поискового характера.


  1. Тип урока: урок изучения и первичного закрепления новых знаний

  2. Формы работы учащихся: индивидуальная, фронтальная, парная

  3. Необходимое техническое оборудование: компьютеры по количеству учащихся, интерактивная доска, графическая оболочка wxMaxima, карточки с заданиями, раздаточный материал.

  4. Структура и ход урока:



№
Этап урока
Деятельность учителя
Деятельность учащихся
Формирование УУД

Познавательные
Регулятивные
Личностные и коммуникативные

1
2
3
4
5
6
7

1
Организационный момент: тема; цель; задачи; мотивация их принятия; планируемые результаты.

Проверяет готовность к уроку. Создаёт положительный эмоциональный настрой на учебную деятельность.
Включаются в деловой ритм урока.






самоопределение; планирование учебного сотрудничества с учителем и сверстниками

2
Актуализация знаний и умений


Организует повторение материала:

1) В какой координатной четверти расположены точки, соответствующие комплексным числам z1=1+2i; z2=-2+5i; z3=-3-2i; z4, если ?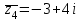

2) Решите уравнения:

а) zRe z=1;

б) z Re z =-1;

в) z Im z =i;

г) z Im z =-i
Отвечают устно на вопросы учителя.
моделирование; знание геометрической модели множества комплексных чисел
оценка (осознание качества и уровня усвоения)
развитие устной научной речи, умение слушать и говорить




Целеполагание и мотивация
Создаёт проблемную ситуацию.

Пусть точка С соответствует некоторому комплексному числу.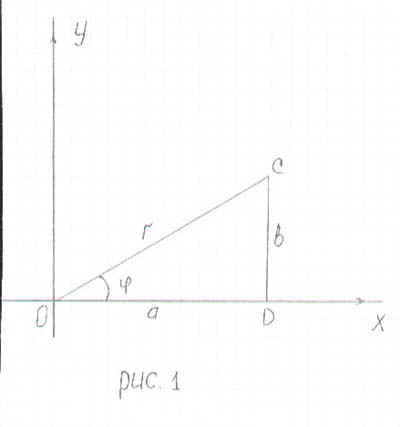

∆ОСD – прямоугольный 

а = ОСcos,

b = ОСsin.

Ответить на вопросы:

Если в алгебраическую запись комплексного числа подставить эти равенства, то мы сможем получить новую запись числа?

А как она, по-вашему мнению будет называться, если в ней присутствуют тригонометрические функции? Так какая же тема урока сегодня? Какая цель нашего урока?
Формулируют тему урока. Формулируют цель: изучение понятия тригонометрическая запись комплексного числа; изучение системы аналитических вычислений wxMaxima.
формулирование информационного запроса;

самостоятельное выделение-формулирование цели урока
уметь ставить учебную задачу на основе соотнесения того, что уже известно и усвоено, и того, что ещё неизвестно
проявление интереса к новому содержанию постановка вопросов; участие в коллективном обсуждении вопроса; уметь устанавливать связи между целью учебной деятельности и её мотивом; умеют аргументировать своё мнение

3

Усвоение новых знаний и способов действий
Разъясняет базовые знания:

Любое комплексное число (кроме нуля) 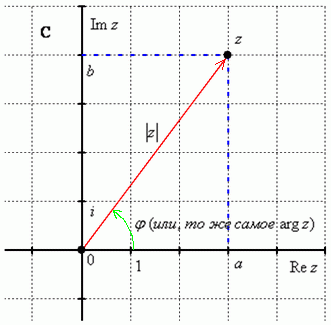 можно записать в тригонометрической форме:
, где  – это модуль комплексного числа, а  – аргумент комплексного числа. Изобразим на комплексной плоскости число . Для определённости и простоты объяснений расположим его в первой координатной четверти, т.е. считаем, что :


Модулем комплексного числа  называется расстояние от начала координат до соответствующей точки комплексной плоскости.

Модуль комплексного числа  стандартно обозначают:  или . По теореме Пифагора легко вывести формулу для нахождения модуля комплексного числа: .

Аргументом комплексного числа  называется угол  между положительной полуосью действительной оси  и радиус-вектором, проведенным из начала координат к соответствующей точке. Аргумент не определён для единственного числа: .

Аргумент комплексного числа  стандартно обозначают:  или . Из геометрических соображений получается следующая формула для нахождения аргумента:
. Формулы для нахождения аргумента будут разными, это зависит от того, в какой координатной четверти лежит число .

1) Если  (1-ая и 4-ая координатные четверти), то аргумент нужно находить по формуле .

2) Если  (2-ая координатная четверть), то аргумент нужно находить по формуле .

3) Если  (3-я координатная четверть), то аргумент нужно находить по формуле .
Фиксируют в тетради основные понятия.
знание понятие тригонометрической формы комплексного число, условия нахождения аргумента в зависимости от того, в какой координатной четверти лежит число .


умение аналитически мыслить, устанавливать причинно-следственные связи
умение планировать учебное сотрудничество с учителем и сверстниками

4

Организация первичного закрепления
Предлагает выполнить задания при комментированном решении. Рассмотрим простейшие примеры, когда комплексные числа располагаются на координатных осях.

1) Представим в тригонометрической форме число .

2) Представим в тригонометрической форме число .

3) Представим в тригонометрической форме число .

4) Представим в тригонометрической форме число .

Внимание! Ни в коем случае нельзя использовать четность косинуса, нечетность синуса и проводить дальнейшее «упрощение» записи.

5) Представим в тригонометрической форме число .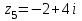
Работают в тетради индивидуально. По одному человеку выходят к доске.

1) Найдем его модуль и аргумент. Расчет по формуле: ,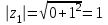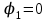

(число лежит на действительной положительной полуоси). Таким образом, число в тригонометрической форме: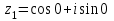


2) ,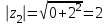  

3) ,

.

4) , ,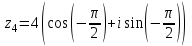



5) Поскольку 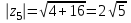 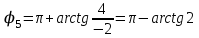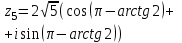(случай 2), то


Выполняют №34.11; №34.14; №34.23
построение логической цепи рассуждений; создание способов решения проблем
контроль (сличения способа действия и его результата с заданным эталоном); оценка (осознание того, что уже усвоено и что ещё подлежит усвоению); волевая саморегуляция
инициативное сотрудничество в поиске и сборе информации

5

Первичная проверка понимания учащимися нового учебного материала.
Выявляет пробелы изученного материала, корректирует выявленные пробелы, обеспечивая закрепление в памяти детей знаний и способов действий.

Самостоятельная работа в парах.Одна работа на двоих. Необходимо рационально распределить задания друг с другом, чтобы успеть выполнить работу.

Учитель выписывает правильные ответы на доску для конечной самопроверки.

Карточка 1: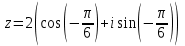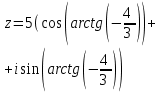



Карточка 2: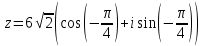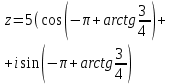
Решают типовых  задания.

Карточка 1:

Выполнить №34.1 (а,в)

Запишите комплексное число в стандартной тригонометрической форме:

а) , б) .

Карточка 2:

Выполнить №34.1 (б,г)

Запишите комплексное число в стандартной тригонометрической форме:

а) , б) .

Выполняют взаимопроверку, путём обмена тетрадями и проверяют по ответам, предложенным учителем и учебником.
умение структуировать знания
контроль, коррекция, самоконтроль и оценка одноклассника.
управление поведением партнера, контроль, коррекция, оценка действий партнера.

6

Закрепление изученного материала.
Сообщает, что контроль правильности выполнения задания можно осуществлять с помощью системы аналитических вычислений wxMaxima.

Разъясняет: Комплексное число в Maxima определено в алгебраической форме с помощью сложения действительной части выражения и произведения %i (мнимой единицы) и мнимой части. Вычисление модуля комплексного числа осуществляется функцией cabs. Аргумент комплексного выражения вычисляется при помощи функции carg. Комплексный аргумент - θ в пределах [−π, π] таким образом, что r exp (тета %i) = z где r - модуль комплексного числа z. Следует учитывать, что carg - вычислительная функция, не предназначенная для упрощения комплексных выражений.

Пример: Вычислить модуль и аргумент комплексных чисел а) 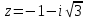; б) z=12;

в)z=-4; г) z=2+3i

Вычислим модуль данных чисел. а)Наберите: cabs(-1-%i*sqrt(3)) (модуль этого комплексного числа равен 2).

А теперь вычислим аргумент этих чисел. а)Наберите: carg(-1-%i*sqrt(3)) (аргумент числа ).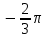
Ведут запись в тетради.

Набирают и получают:



Выполняют №34.24 в Maxima.
умение применять систему аналитических вычислений wxMaxima; установление причинно-следственных связей
преобразовывать практическую задачу в учебно-познавательную; совместно с учителем прогнозирование результата;
сотрудничество в поиске и сборе информации; оценивание усваиваемого содержания; осуществлять рефлексию своего отношения к содержанию темы

7

Обобщение и систематизация знаний.
Выявляет качество и уровень усвоения знаний и способов действий, а также недостатки в знаниях и способах действий, устанавливает причины выявленных недостатков.Контроль темы проводит в форме индивидуального выполнения проверочной работы.

Выполняют проверочную работу. Ведут запись в тетради. Делают проверку на комьютере в системе аналитических вычислений wxMaxima.
Вариант 1:

№1. Запишите комплексное число в стандартной тригонометрической форме: а)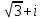

б) .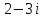

№2. Изобразите на координатной плоскости множество точек z, удовлетворяющих условию а) ;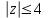

б) .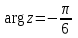

Вариант 2:

№1. Запишите комплексное число в стандартной тригонометрической форме: а)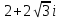

б) .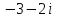

№2 . Изобразите на координатной плоскости множество точек z, удовлетворяющих условию а) ;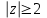

б) .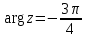
умение осознанно применять алгоритм
умение проявлять способность к мобилизации сил и энергии
уметь с достаточной полнотой и точностью выражать свои мысли в соответствии с задачами и условиями

8

Подведение итогов: диагностика результатов урока, рефлексия достижения цели.
Предлагает каждому учащемуся высказать свое мнение в виде фраз, начиная ее словами:

  1. сегодня я узнал…

  2. было трудно…

  3. я понял, что…

  4. теперь я могу… и ответить на вопросы: - Что понравилось на уроке? - Достигли ли мы поставленных целей?

Оценить отдельных учащихся.

Проверить и оценить выполнение письменной проверочной работы.

Осуществляют самооценку учебной деятельности, соотносят цель и результаты

Отвечают на вопросы учителя: что узнали, чему научились и т.д.



выделение и осознание степени усвоения материала
умение с достаточной полнотой и точностью выражать свои мысли и эмоции

9

Домашнее задание и инструктаж по его выполнению.
Обеспечивает понимания детьми цели, содержания и способов выполнения домашнего задания.

Д/ з: п. 34; №34.5; №34.15 (а,в); №34.22; №34.25
Записывают в дневники домашнее задание.

 






умение работать с учебником

Смотрите также файлы