Файл: Лабораторная работа 13 Изучение различных преобразователей двоичных сигналов Цель работы.docx
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 11.01.2024
Просмотров: 15
Скачиваний: 1
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
ЛАБОРАТОРНАЯ РАБОТА № 13
Изучение различных преобразователей двоичных сигналов
1. Цель работы
Изучение способов построения преобразователей сигналов двоичного кода на все сочетания в специальные и помехозащищенные коды и обратно.
2. Общие сведения
Преобразователями кодов называются устройства, служащие для перевода n-элементного параллельного кода на входе в m-элементный параллельный код на выходе. На рис.1 представлено условное обозна-чение преобразователя кодов. Частным случаем преобразователей кодов являются шифраторы и дешифраторы. Преобразователи кодов, не являющиеся шифраторам или дешифраторам, называют трансляторами кодов или, собственно, преобразователями кодов.
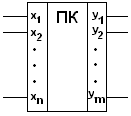
Рис.1. Условное обозначение преобразователя кодов
Обычный подход к построению транслятора кодов основан на представлении его в виде комбинационного устройства с несколькими входами и выходами. Рассмотрим этот метод на примере преобразования двоичного кода на все сочетания в равновесный код “2 из 4” (код “m из n”).
Пусть на вход преобразователя поступают комбинации двоичного кода для десятичных чисел [О, I, 2, 3, 4, 5], которым соответствуют комбинации кода “2 из 4” для десятичных чисел [3, 5, 9, 6, 10, I2]. Тогда преобразователь имеет три входа Х1, Х2 и Х3, соответствующие разрядам двоичного кода, и четыре выхода: y1‚ y2, y3, и y4, соответствующие разрядам кода “2 из 4”. Предполагается, что неиспользованные комбинации двоичного кода чисел {6, 7} на вход преобразователя не подаются и значение выходов при этом безразлично. На основании задания для разработки дискретного устройства составим таблицу истинности ТИ (табл.1).
Таблица 1
№
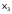
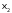
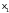
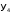
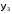
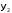
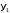
0
0
0
0
0
0
1
1
1
0
0
1
0
1
0
1
2
0
1
0
1
0
0
1
3
0
1
1
0
1
1
0
4
1
0
0
1
0
1
0
5
1
0
1
1
1
0
0
6
1
1
0
7
1
1
1
Таблица истинности имеет число столбцов, равное сумме входов и выходов и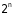 
строк, где n-число входов. Каждая строка таблицы истинности соответствует одному из входных наборов, причем десятичному номеру строки соответствует двоичный набор входных переменных.
По условию задачи входному набору 0 соответствует выходной набор 3. Это означает, что в данной строке в столбцах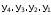 
проставляется код 0011, соответствующий числу 3; входному набору 1 соответствует выходной набор 5 - 0101 и т.д. Входные наборы {6, 7} не подаются, поэтому в строках, соответствующих этим наборам на пересечении со столбцами 
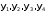, проставляется знак "
", означающий безразличное состояние (0 или I). В дальнейшем, на этапе минимизации целесообразно учитывать безразличные состояния, что позволяет получить более простые функции.
Составим по ТИ переключательные (выходные) функции схемы.
Функции выходов могут быть вычислены как по разрешенным наборам (в виде СДНФ), так и по запрещенным наборам (в виде СКНФ). Запишем выходные функции в виде СДНФ.
Произведем минимизацию функций по картам Карно. Особенностью минимизации является наличие в таблице истинности безразличных состояний. Ввиду недостижимости этих состояний при нормальной работе схемы им можно поставить в соответствие любое значение: либо 0, либо I. Для получения более простой функции целесообразно безразличным состояниям задавать такие значения, при которых в карте Карно получаются контуры с максимально возможным числом клеток.
Для примера имеем следующие карты Карно (рис.2). В карте функции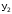 
клетка, соответствующая набору 
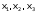, включена в контур с разрешенными наборами, следовательно, и на наборе 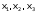функция 
.
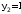Вид карты Карно для четырех и пяти переменных показан на рис.3.
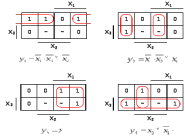
Рис.2. Карты Карно для трех переменных
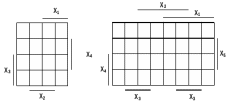
Рис.3. Карты Карно для четырех и пяти переменных
Реализация полученных функций преобразователя кодов производится в указанном преподавателем элементном базисе. В связи с этим реальная схема дискретного устройства должна быть пересчитана и составлена на заданный тип элементов. Реализацию следует производить в виде единой схемы, имеющей общие элементы для разных функций (см. рис. 4).
В данной лабораторной работе этот этап синтеза практически не рассматривается, а производится только сборка синтезированной схемы в поле программы Proteus 7.0. и её испытание.
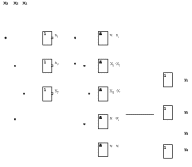
Рис.4. Схема преобразователя кодов
Для подключения цифровых, например, семисегментных свето-диодных индикаторов, требуется специальный преобразователь (рис.5) двоичного кода на все сочетания в код этого индикатора (к ним относятся, например, ИМС 7447 и 7448 из серии TTL74 – аналоги отечественных ИМС 514ИД1 и 514ИД2), когда число светящихся сегментов может быть от двух (для цифры 1) до семи (для цифры 8). Поскольку число входов преобразователя равно четырем (для кодирования десятичных чисел 0-9 достаточно иметь 4-х разрядный двоичный код), а число выходов равно семи (по числу сегментов), то таблица истинности этого преобразователя содержит 11 столбцов и 10 строк (число десятичных цифр). Система переключательных функций, описывающих схему преобразователя будет содержать семь уравнений.
Из рис.5 следует, что, например, в цифре 0 должны светиться все сегменты, кроме сегмента G. Студентам предлагается самим построить ТИ данного преобразователя кодов, составить по ТИ переключательные (выходные) функции схемы, используя карты Карно для четырех переменных, произвести минимизацию полученных ПФ, собрать синтезированную схему преобразователя в поле программы Proteus 7.0. и провести её испытание.
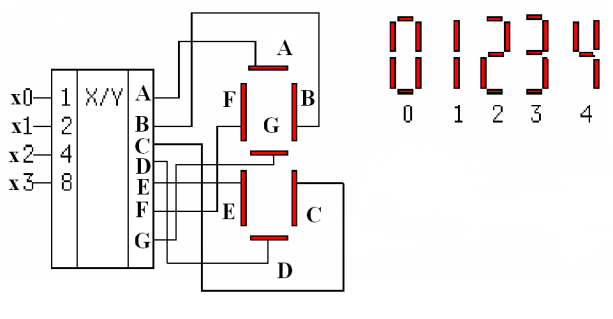
Рис. 5. Преобразоватеь кода “4 в 7” и подключение индикатора
3. Описание рабочего места
Работа выполняется на компьютере, в программе Proteus 7.0 Сигналы логического «0» и «1» от аргументов Х задаются в ручном режиме. Графические изображения элементов с заданным числом входов, реализующих исследуемые функции, выбираются из окна библиотеки компонентов (подкатегория Modeling Primitives). При составлении схем соединение элементов производится вручную с помощью «мыши». Значения сигналов определяются через логический пробник или осциллограф, которые можно подключать к выходам исследуемой схемы.
4. Задание к лабораторной работе
1. Изучить основные этапы синтеза комбинационных схем.
2. Изучить основные этапы синтеза преобразователей кодов.
3.Провести синтез преобразователя кодов для варианта, указанного преподавателем.
4. Составить и собрать схему преобразователя кодов на компьютере в поле программы Proteus 7.0 и провести анализ её работы.
Варианты заданий
Задание 1. Произвести синтез преобразователя кода из двоичного в код "2 из 5".
Преобразователь имеет четыре входа: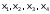 
, соответствующие разрядам двоичного кода, и пять выходов: 
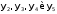, соответствующие разрядам кода "2 из 5".
Зависимость выходных комбинаций кода "2 из 3" от входных комбинаций двоичного кода представлена в табл.2.
Таблица 2
№
Вход преобразователя
Выход преобразователя
Запрещенные комби-нации
Двоичный код
Код “2 из 5”
Двоичный код
1
0,1,2,3,4,5,6,7,8,9
3,5,9,17,6,10,18,12,20,24
10,11,12,13,14
2
0,1,4,5,8,9,10,11,14,15
3,9,6,18,5,17,10,24,20,12
2,3,6,7,12,13
3
6,7,8,9,10,11,12,13,14,15
24,20,12,18,10,6,17,9,5,3
0,1,2,3,4,5
4
0,1,2,3,4,11,12,13,14,15
5,17,10,12,24,3,9,6,18,20
5,6,7,8,9,10
Предполагается, что неиспользуемые (запрещенные) комбинации двоичного кода на вход преобразователя не подаются и значение выходов при этом безразлично.
Задание 2. Произвести синтез преобразователя двоичного кода в код с проверкой на нечетность.
Преобразователь имеет четыре входа 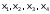, соответствующие разрядам двоичного кода, и пять выходов 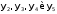, соответствующие разрядам кода с проверкой на нечетность. Предполагается, что запрещенные комбинации двоичного кода на вход преобразователя не подаются (табл.3).
Таблица 3
№
Вход преобразователя
Выход преобразователя
Запрещенные комбинации
Двоичный код
Код c проверкой на нечетность
Двоичный
код
1
0,1,2,3,4,5,6,7,8,9
16,1,2,19,4,21,22,7,8,25
10,11,12,13,14
2
0,1,4,5,8,9,10,11,14,15
22,7,8,25,26,11,28,13,14,31
2,3,6,7,12,13
3
6,7,8,9,10,11,12,13,14,15
16,1,21,9,4,11,28,13,14,31
0,1,2,3,4,5
4
0,1,2,3,4,11,12,13,14,15
16,1,4,21,8,25,28,13,14,31
5,6,7,8,9,10
Задание 3. Произвести синтез преобразователя двоичного кода в код для семисегментного светодиодного индикатора.
Преобразователь имеет четыре входа 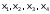, соответствующие разрядам двоичного кода, и семь выходов: 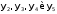, соответствующих количеству сегментов индикатора. Предполагается, что на вход преобразователя подаются только комбинации двоичного кода, соответствующие десятичным числам от 0 до 9.
Задание 4. Выбрать из библиотеки компонентов ИМС (серия TTL 74, подкатегория Decoders) по указанию преподавателя, один из преобразователей (7447, 7448 или 74247), исследовать его работу и составить таблицу истинности.
5. Указания к выполнению работы
1. Составить таблицу истинности преобразователя кодов по предложенному варианту (табл. 2 ÷ табл.4).
2. Составить по ТИ переключательные функции схемы в виде СДНФ.
3. Минимизировать полученные функции по картам Карно
4. По полученной минимизированной форме функции составить схему преобразователя.
5. Собрать составленную схему устройства в поле программы Proteus 7.0. Если рассматриваемая переменная входит в конъюнкцию со знаком инверсии, то сигнал на вход элемента И подаётся через инвертор.
6. Проанализировать работу схемы на соответствие заданной таблице истинности. Для этого, задавая значения входных сигналов аргументов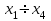 
при помощи логических имитаторов LOGIGSTATE, набрать по очереди все комбинации значений входных переменных и пользуясь логическими пробниками LOGICPROBE, многоканальным логическим анализатором LOGIC ANALIYSER или осциллографом, записать соответствующие значения выходов схемы.
6. Содержание отчёта
В отчете необходимо отразить: 1. Цель работы; 2. Заданную переключательную функцию в виде СДНФ; 3. Ход минимизации ПФ;
4.Полученную минимальную форму ПФ; 5. Схему минимизированной формы ПФ в заданном элементном базисе; 6. Результаты проверки схемы преобразователя (или ИМС) в виде таблицы истинности.
7. Контрольные вопросы
1. На каких законах алгебры логики основывается минимизация методом карт Карно?
2. Почему при минимизации безразличным состояниям в ТИ можно поставить в соответствие любое значение переменной – либо 0, либо 1?
3. Какие устройства называются трансляторами кодов?
4. Чему равно число столбцов таблицы истинности преобразователя двоичного кода на все сочетания в код “m из n”?
5. Почему преобразователь двоичного кода в код с проверкой на нечетность имеет четыре входа и пять выходов?
6. Какие устройства являются частными случаями преобразователей кодов?
ЛАБОРАТОРНАЯ РАБОТА № 13
Изучение различных преобразователей двоичных сигналов
1. Цель работы
Изучение способов построения преобразователей сигналов двоичного кода на все сочетания в специальные и помехозащищенные коды и обратно.
2. Общие сведения
Преобразователями кодов называются устройства, служащие для перевода n-элементного параллельного кода на входе в m-элементный параллельный код на выходе. На рис.1 представлено условное обозна-чение преобразователя кодов. Частным случаем преобразователей кодов являются шифраторы и дешифраторы. Преобразователи кодов, не являющиеся шифраторам или дешифраторам, называют трансляторами кодов или, собственно, преобразователями кодов.
Рис.1. Условное обозначение преобразователя кодов
Обычный подход к построению транслятора кодов основан на представлении его в виде комбинационного устройства с несколькими входами и выходами. Рассмотрим этот метод на примере преобразования двоичного кода на все сочетания в равновесный код “2 из 4” (код “m из n”).
Пусть на вход преобразователя поступают комбинации двоичного кода для десятичных чисел [О, I, 2, 3, 4, 5], которым соответствуют комбинации кода “2 из 4” для десятичных чисел [3, 5, 9, 6, 10, I2]. Тогда преобразователь имеет три входа Х1, Х2 и Х3, соответствующие разрядам двоичного кода, и четыре выхода: y1‚ y2, y3, и y4, соответствующие разрядам кода “2 из 4”. Предполагается, что неиспользованные комбинации двоичного кода чисел {6, 7} на вход преобразователя не подаются и значение выходов при этом безразлично. На основании задания для разработки дискретного устройства составим таблицу истинности ТИ (табл.1).
Таблица 1
№
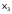
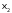
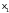
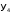
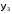
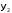
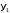
0
0
0
0
0
0
1
1
1
0
0
1
0
1
0
1
2
0
1
0
1
0
0
1
3
0
1
1
0
1
1
0
4
1
0
0
1
0
1
0
5
1
0
1
1
1
0
0
6
1
1
0
7
1
1
1
Таблица истинности имеет число столбцов, равное сумме входов и выходов и 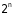строк, где n-число входов. Каждая строка таблицы истинности соответствует одному из входных наборов, причем десятичному номеру строки соответствует двоичный набор входных переменных.
По условию задачи входному набору 0 соответствует выходной набор 3. Это означает, что в данной строке в столбцах 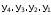проставляется код 0011, соответствующий числу 3; входному набору 1 соответствует выходной набор 5 - 0101 и т.д. Входные наборы {6, 7} не подаются, поэтому в строках, соответствующих этим наборам на пересечении со столбцами 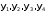, проставляется знак "
", означающий безразличное состояние (0 или I). В дальнейшем, на этапе минимизации целесообразно учитывать безразличные состояния, что позволяет получить более простые функции.
Составим по ТИ переключательные (выходные) функции схемы.
Функции выходов могут быть вычислены как по разрешенным наборам (в виде СДНФ), так и по запрещенным наборам (в виде СКНФ). Запишем выходные функции в виде СДНФ.
Произведем минимизацию функций по картам Карно. Особенностью минимизации является наличие в таблице истинности безразличных состояний. Ввиду недостижимости этих состояний при нормальной работе схемы им можно поставить в соответствие любое значение: либо 0, либо I. Для получения более простой функции целесообразно безразличным состояниям задавать такие значения, при которых в карте Карно получаются контуры с максимально возможным числом клеток.
Для примера имеем следующие карты Карно (рис.2). В карте функции 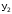клетка, соответствующая набору 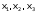, включена в контур с разрешенными наборами, следовательно, и на наборе 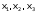функция .
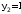Вид карты Карно для четырех и пяти переменных показан на рис.3.
Рис.2. Карты Карно для трех переменных
Рис.3. Карты Карно для четырех и пяти переменных
Реализация полученных функций преобразователя кодов производится в указанном преподавателем элементном базисе. В связи с этим реальная схема дискретного устройства должна быть пересчитана и составлена на заданный тип элементов. Реализацию следует производить в виде единой схемы, имеющей общие элементы для разных функций (см. рис. 4).
В данной лабораторной работе этот этап синтеза практически не рассматривается, а производится только сборка синтезированной схемы в поле программы Proteus 7.0. и её испытание.
Рис.4. Схема преобразователя кодов
Для подключения цифровых, например, семисегментных свето-диодных индикаторов, требуется специальный преобразователь (рис.5) двоичного кода на все сочетания в код этого индикатора (к ним относятся, например, ИМС 7447 и 7448 из серии TTL74 – аналоги отечественных ИМС 514ИД1 и 514ИД2), когда число светящихся сегментов может быть от двух (для цифры 1) до семи (для цифры 8). Поскольку число входов преобразователя равно четырем (для кодирования десятичных чисел 0-9 достаточно иметь 4-х разрядный двоичный код), а число выходов равно семи (по числу сегментов), то таблица истинности этого преобразователя содержит 11 столбцов и 10 строк (число десятичных цифр). Система переключательных функций, описывающих схему преобразователя будет содержать семь уравнений.
Из рис.5 следует, что, например, в цифре 0 должны светиться все сегменты, кроме сегмента G. Студентам предлагается самим построить ТИ данного преобразователя кодов, составить по ТИ переключательные (выходные) функции схемы, используя карты Карно для четырех переменных, произвести минимизацию полученных ПФ, собрать синтезированную схему преобразователя в поле программы Proteus 7.0. и провести её испытание.
Рис. 5. Преобразоватеь кода “4 в 7” и подключение индикатора
3. Описание рабочего места
Работа выполняется на компьютере, в программе Proteus 7.0 Сигналы логического «0» и «1» от аргументов Х задаются в ручном режиме. Графические изображения элементов с заданным числом входов, реализующих исследуемые функции, выбираются из окна библиотеки компонентов (подкатегория Modeling Primitives). При составлении схем соединение элементов производится вручную с помощью «мыши». Значения сигналов определяются через логический пробник или осциллограф, которые можно подключать к выходам исследуемой схемы.
4. Задание к лабораторной работе
1. Изучить основные этапы синтеза комбинационных схем.
2. Изучить основные этапы синтеза преобразователей кодов.
3.Провести синтез преобразователя кодов для варианта, указанного преподавателем.
4. Составить и собрать схему преобразователя кодов на компьютере в поле программы Proteus 7.0 и провести анализ её работы.
Варианты заданий
Задание 1. Произвести синтез преобразователя кода из двоичного в код "2 из 5".
Преобразователь имеет четыре входа: 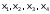, соответствующие разрядам двоичного кода, и пять выходов: 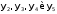, соответствующие разрядам кода "2 из 5".
Зависимость выходных комбинаций кода "2 из 3" от входных комбинаций двоичного кода представлена в табл.2.
Таблица 2
№
Вход преобразователя
Выход преобразователя
Запрещенные комби-нации
Двоичный код
Код “2 из 5”
Двоичный код
1
0,1,2,3,4,5,6,7,8,9
3,5,9,17,6,10,18,12,20,24
10,11,12,13,14
2
0,1,4,5,8,9,10,11,14,15
3,9,6,18,5,17,10,24,20,12
2,3,6,7,12,13
3
6,7,8,9,10,11,12,13,14,15
24,20,12,18,10,6,17,9,5,3
0,1,2,3,4,5
4
0,1,2,3,4,11,12,13,14,15
5,17,10,12,24,3,9,6,18,20
5,6,7,8,9,10
Предполагается, что неиспользуемые (запрещенные) комбинации двоичного кода на вход преобразователя не подаются и значение выходов при этом безразлично.
Задание 2. Произвести синтез преобразователя двоичного кода в код с проверкой на нечетность.
Преобразователь имеет четыре входа 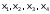, соответствующие разрядам двоичного кода, и пять выходов 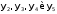, соответствующие разрядам кода с проверкой на нечетность. Предполагается, что запрещенные комбинации двоичного кода на вход преобразователя не подаются (табл.3).
Таблица 3
№
Вход преобразователя
Выход преобразователя
Запрещенные комбинации
Двоичный код
Код c проверкой на нечетность
Двоичный
код
1
0,1,2,3,4,5,6,7,8,9
16,1,2,19,4,21,22,7,8,25
10,11,12,13,14
2
0,1,4,5,8,9,10,11,14,15
22,7,8,25,26,11,28,13,14,31
2,3,6,7,12,13
3
6,7,8,9,10,11,12,13,14,15
16,1,21,9,4,11,28,13,14,31
0,1,2,3,4,5
4
0,1,2,3,4,11,12,13,14,15
16,1,4,21,8,25,28,13,14,31
5,6,7,8,9,10
Задание 3. Произвести синтез преобразователя двоичного кода в код для семисегментного светодиодного индикатора.
Преобразователь имеет четыре входа 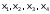, соответствующие разрядам двоичного кода, и семь выходов: 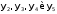, соответствующих количеству сегментов индикатора. Предполагается, что на вход преобразователя подаются только комбинации двоичного кода, соответствующие десятичным числам от 0 до 9.
Задание 4. Выбрать из библиотеки компонентов ИМС (серия TTL 74, подкатегория Decoders) по указанию преподавателя, один из преобразователей (7447, 7448 или 74247), исследовать его работу и составить таблицу истинности.
5. Указания к выполнению работы
1. Составить таблицу истинности преобразователя кодов по предложенному варианту (табл. 2 ÷ табл.4).
2. Составить по ТИ переключательные функции схемы в виде СДНФ.
3. Минимизировать полученные функции по картам Карно
4. По полученной минимизированной форме функции составить схему преобразователя.
5. Собрать составленную схему устройства в поле программы Proteus 7.0. Если рассматриваемая переменная входит в конъюнкцию со знаком инверсии, то сигнал на вход элемента И подаётся через инвертор.
6. Проанализировать работу схемы на соответствие заданной таблице истинности. Для этого, задавая значения входных сигналов аргументов 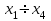при помощи логических имитаторов LOGIGSTATE, набрать по очереди все комбинации значений входных переменных и пользуясь логическими пробниками LOGICPROBE, многоканальным логическим анализатором LOGIC ANALIYSER или осциллографом, записать соответствующие значения выходов схемы.
6. Содержание отчёта
В отчете необходимо отразить: 1. Цель работы; 2. Заданную переключательную функцию в виде СДНФ; 3. Ход минимизации ПФ;
4.Полученную минимальную форму ПФ; 5. Схему минимизированной формы ПФ в заданном элементном базисе; 6. Результаты проверки схемы преобразователя (или ИМС) в виде таблицы истинности.
7. Контрольные вопросы
1. На каких законах алгебры логики основывается минимизация методом карт Карно?
2. Почему при минимизации безразличным состояниям в ТИ можно поставить в соответствие любое значение переменной – либо 0, либо 1?
3. Какие устройства называются трансляторами кодов?
4. Чему равно число столбцов таблицы истинности преобразователя двоичного кода на все сочетания в код “m из n”?
5. Почему преобразователь двоичного кода в код с проверкой на нечетность имеет четыре входа и пять выходов?
6. Какие устройства являются частными случаями преобразователей кодов?
ЛАБОРАТОРНАЯ РАБОТА № 13
Изучение различных преобразователей двоичных сигналов
1. Цель работы
Изучение способов построения преобразователей сигналов двоичного кода на все сочетания в специальные и помехозащищенные коды и обратно.
2. Общие сведения
Преобразователями кодов называются устройства, служащие для перевода n-элементного параллельного кода на входе в m-элементный параллельный код на выходе. На рис.1 представлено условное обозна-чение преобразователя кодов. Частным случаем преобразователей кодов являются шифраторы и дешифраторы. Преобразователи кодов, не являющиеся шифраторам или дешифраторам, называют трансляторами кодов или, собственно, преобразователями кодов.
Рис.1. Условное обозначение преобразователя кодов
Обычный подход к построению транслятора кодов основан на представлении его в виде комбинационного устройства с несколькими входами и выходами. Рассмотрим этот метод на примере преобразования двоичного кода на все сочетания в равновесный код “2 из 4” (код “m из n”).
Пусть на вход преобразователя поступают комбинации двоичного кода для десятичных чисел [О, I, 2, 3, 4, 5], которым соответствуют комбинации кода “2 из 4” для десятичных чисел [3, 5, 9, 6, 10, I2]. Тогда преобразователь имеет три входа Х1, Х2 и Х3, соответствующие разрядам двоичного кода, и четыре выхода: y1‚ y2, y3, и y4, соответствующие разрядам кода “2 из 4”. Предполагается, что неиспользованные комбинации двоичного кода чисел {6, 7} на вход преобразователя не подаются и значение выходов при этом безразлично. На основании задания для разработки дискретного устройства составим таблицу истинности ТИ (табл.1).
Таблица 1
№
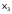
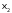
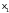
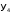
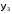
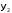
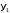
0
0
0
0
0
0
1
1
1
0
0
1
0
1
0
1
2
0
1
0
1
0
0
1
3
0
1
1
0
1
1
0
4
1
0
0
1
0
1
0
5
1
0
1
1
1
0
0
6
1
1
0
7
1
1
1
Таблица истинности имеет число столбцов, равное сумме входов и выходов и 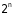строк, где n-число входов. Каждая строка таблицы истинности соответствует одному из входных наборов, причем десятичному номеру строки соответствует двоичный набор входных переменных.
По условию задачи входному набору 0 соответствует выходной набор 3. Это означает, что в данной строке в столбцах 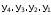проставляется код 0011, соответствующий числу 3; входному набору 1 соответствует выходной набор 5 - 0101 и т.д. Входные наборы {6, 7} не подаются, поэтому в строках, соответствующих этим наборам на пересечении со столбцами 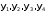, проставляется знак "
", означающий безразличное состояние (0 или I). В дальнейшем, на этапе минимизации целесообразно учитывать безразличные состояния, что позволяет получить более простые функции.
Составим по ТИ переключательные (выходные) функции схемы.
Функции выходов могут быть вычислены как по разрешенным наборам (в виде СДНФ), так и по запрещенным наборам (в виде СКНФ). Запишем выходные функции в виде СДНФ.
Произведем минимизацию функций по картам Карно. Особенностью минимизации является наличие в таблице истинности безразличных состояний. Ввиду недостижимости этих состояний при нормальной работе схемы им можно поставить в соответствие любое значение: либо 0, либо I. Для получения более простой функции целесообразно безразличным состояниям задавать такие значения, при которых в карте Карно получаются контуры с максимально возможным числом клеток.
Для примера имеем следующие карты Карно (рис.2). В карте функции 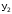клетка, соответствующая набору 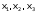, включена в контур с разрешенными наборами, следовательно, и на наборе 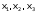функция .
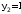Вид карты Карно для четырех и пяти переменных показан на рис.3.
Рис.2. Карты Карно для трех переменных
Рис.3. Карты Карно для четырех и пяти переменных
Реализация полученных функций преобразователя кодов производится в указанном преподавателем элементном базисе. В связи с этим реальная схема дискретного устройства должна быть пересчитана и составлена на заданный тип элементов. Реализацию следует производить в виде единой схемы, имеющей общие элементы для разных функций (см. рис. 4).
В данной лабораторной работе этот этап синтеза практически не рассматривается, а производится только сборка синтезированной схемы в поле программы Proteus 7.0. и её испытание.
Рис.4. Схема преобразователя кодов
Для подключения цифровых, например, семисегментных свето-диодных индикаторов, требуется специальный преобразователь (рис.5) двоичного кода на все сочетания в код этого индикатора (к ним относятся, например, ИМС 7447 и 7448 из серии TTL74 – аналоги отечественных ИМС 514ИД1 и 514ИД2), когда число светящихся сегментов может быть от двух (для цифры 1) до семи (для цифры 8). Поскольку число входов преобразователя равно четырем (для кодирования десятичных чисел 0-9 достаточно иметь 4-х разрядный двоичный код), а число выходов равно семи (по числу сегментов), то таблица истинности этого преобразователя содержит 11 столбцов и 10 строк (число десятичных цифр). Система переключательных функций, описывающих схему преобразователя будет содержать семь уравнений.
Из рис.5 следует, что, например, в цифре 0 должны светиться все сегменты, кроме сегмента G. Студентам предлагается самим построить ТИ данного преобразователя кодов, составить по ТИ переключательные (выходные) функции схемы, используя карты Карно для четырех переменных, произвести минимизацию полученных ПФ, собрать синтезированную схему преобразователя в поле программы Proteus 7.0. и провести её испытание.
Рис. 5. Преобразоватеь кода “4 в 7” и подключение индикатора
3. Описание рабочего места
Работа выполняется на компьютере, в программе Proteus 7.0 Сигналы логического «0» и «1» от аргументов Х задаются в ручном режиме. Графические изображения элементов с заданным числом входов, реализующих исследуемые функции, выбираются из окна библиотеки компонентов (подкатегория Modeling Primitives). При составлении схем соединение элементов производится вручную с помощью «мыши». Значения сигналов определяются через логический пробник или осциллограф, которые можно подключать к выходам исследуемой схемы.
4. Задание к лабораторной работе
1. Изучить основные этапы синтеза комбинационных схем.
2. Изучить основные этапы синтеза преобразователей кодов.
3.Провести синтез преобразователя кодов для варианта, указанного преподавателем.
4. Составить и собрать схему преобразователя кодов на компьютере в поле программы Proteus 7.0 и провести анализ её работы.
Варианты заданий
Задание 1. Произвести синтез преобразователя кода из двоичного в код "2 из 5".
Преобразователь имеет четыре входа: 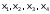, соответствующие разрядам двоичного кода, и пять выходов: 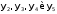, соответствующие разрядам кода "2 из 5".
Зависимость выходных комбинаций кода "2 из 3" от входных комбинаций двоичного кода представлена в табл.2.
Таблица 2
№
Вход преобразователя
Выход преобразователя
Запрещенные комби-нации
Двоичный код
Код “2 из 5”
Двоичный код
1
0,1,2,3,4,5,6,7,8,9
3,5,9,17,6,10,18,12,20,24
10,11,12,13,14
2
0,1,4,5,8,9,10,11,14,15
3,9,6,18,5,17,10,24,20,12
2,3,6,7,12,13
3
6,7,8,9,10,11,12,13,14,15
24,20,12,18,10,6,17,9,5,3
0,1,2,3,4,5
4
0,1,2,3,4,11,12,13,14,15
5,17,10,12,24,3,9,6,18,20
5,6,7,8,9,10
Предполагается, что неиспользуемые (запрещенные) комбинации двоичного кода на вход преобразователя не подаются и значение выходов при этом безразлично.
Задание 2. Произвести синтез преобразователя двоичного кода в код с проверкой на нечетность.
Преобразователь имеет четыре входа 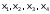, соответствующие разрядам двоичного кода, и пять выходов 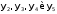, соответствующие разрядам кода с проверкой на нечетность. Предполагается, что запрещенные комбинации двоичного кода на вход преобразователя не подаются (табл.3).
Таблица 3
№
Вход преобразователя
Выход преобразователя
Запрещенные комбинации
Двоичный код
Код c проверкой на нечетность
Двоичный
код
1
0,1,2,3,4,5,6,7,8,9
16,1,2,19,4,21,22,7,8,25
10,11,12,13,14
2
0,1,4,5,8,9,10,11,14,15
22,7,8,25,26,11,28,13,14,31
2,3,6,7,12,13
3
6,7,8,9,10,11,12,13,14,15
16,1,21,9,4,11,28,13,14,31
0,1,2,3,4,5
4
0,1,2,3,4,11,12,13,14,15
16,1,4,21,8,25,28,13,14,31
5,6,7,8,9,10
Задание 3. Произвести синтез преобразователя двоичного кода в код для семисегментного светодиодного индикатора.
Преобразователь имеет четыре входа 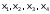, соответствующие разрядам двоичного кода, и семь выходов: 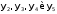, соответствующих количеству сегментов индикатора. Предполагается, что на вход преобразователя подаются только комбинации двоичного кода, соответствующие десятичным числам от 0 до 9.
Задание 4. Выбрать из библиотеки компонентов ИМС (серия TTL 74, подкатегория Decoders) по указанию преподавателя, один из преобразователей (7447, 7448 или 74247), исследовать его работу и составить таблицу истинности.
5. Указания к выполнению работы
1. Составить таблицу истинности преобразователя кодов по предложенному варианту (табл. 2 ÷ табл.4).
2. Составить по ТИ переключательные функции схемы в виде СДНФ.
3. Минимизировать полученные функции по картам Карно
4. По полученной минимизированной форме функции составить схему преобразователя.
5. Собрать составленную схему устройства в поле программы Proteus 7.0. Если рассматриваемая переменная входит в конъюнкцию со знаком инверсии, то сигнал на вход элемента И подаётся через инвертор.
6. Проанализировать работу схемы на соответствие заданной таблице истинности. Для этого, задавая значения входных сигналов аргументов 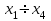при помощи логических имитаторов LOGIGSTATE, набрать по очереди все комбинации значений входных переменных и пользуясь логическими пробниками LOGICPROBE, многоканальным логическим анализатором LOGIC ANALIYSER или осциллографом, записать соответствующие значения выходов схемы.
6. Содержание отчёта
В отчете необходимо отразить: 1. Цель работы; 2. Заданную переключательную функцию в виде СДНФ; 3. Ход минимизации ПФ;
4.Полученную минимальную форму ПФ; 5. Схему минимизированной формы ПФ в заданном элементном базисе; 6. Результаты проверки схемы преобразователя (или ИМС) в виде таблицы истинности.
7. Контрольные вопросы
1. На каких законах алгебры логики основывается минимизация методом карт Карно?
2. Почему при минимизации безразличным состояниям в ТИ можно поставить в соответствие любое значение переменной – либо 0, либо 1?
3. Какие устройства называются трансляторами кодов?
4. Чему равно число столбцов таблицы истинности преобразователя двоичного кода на все сочетания в код “m из n”?
5. Почему преобразователь двоичного кода в код с проверкой на нечетность имеет четыре входа и пять выходов?
6. Какие устройства являются частными случаями преобразователей кодов?
ЛАБОРАТОРНАЯ РАБОТА № 13
Изучение различных преобразователей двоичных сигналов
1. Цель работы
Изучение способов построения преобразователей сигналов двоичного кода на все сочетания в специальные и помехозащищенные коды и обратно.
2. Общие сведения
Преобразователями кодов называются устройства, служащие для перевода n-элементного параллельного кода на входе в m-элементный параллельный код на выходе. На рис.1 представлено условное обозна-чение преобразователя кодов. Частным случаем преобразователей кодов являются шифраторы и дешифраторы. Преобразователи кодов, не являющиеся шифраторам или дешифраторам, называют трансляторами кодов или, собственно, преобразователями кодов.
Рис.1. Условное обозначение преобразователя кодов
Обычный подход к построению транслятора кодов основан на представлении его в виде комбинационного устройства с несколькими входами и выходами. Рассмотрим этот метод на примере преобразования двоичного кода на все сочетания в равновесный код “2 из 4” (код “m из n”).
Пусть на вход преобразователя поступают комбинации двоичного кода для десятичных чисел [О, I, 2, 3, 4, 5], которым соответствуют комбинации кода “2 из 4” для десятичных чисел [3, 5, 9, 6, 10, I2]. Тогда преобразователь имеет три входа Х1, Х2 и Х3, соответствующие разрядам двоичного кода, и четыре выхода: y1‚ y2, y3, и y4, соответствующие разрядам кода “2 из 4”. Предполагается, что неиспользованные комбинации двоичного кода чисел {6, 7} на вход преобразователя не подаются и значение выходов при этом безразлично. На основании задания для разработки дискретного устройства составим таблицу истинности ТИ (табл.1).
Таблица 1
№
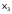
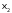
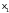
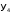
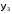
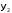
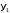
0
0
0
0
0
0
1
1
1
0
0
1
0
1
0
1
2
0
1
0
1
0
0
1
3
0
1
1
0
1
1
0
4
1
0
0
1
0
1
0
5
1
0
1
1
1
0
0
6
1
1
0
7
1
1
1
Таблица истинности имеет число столбцов, равное сумме входов и выходов и 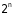строк, где n-число входов. Каждая строка таблицы истинности соответствует одному из входных наборов, причем десятичному номеру строки соответствует двоичный набор входных переменных.
По условию задачи входному набору 0 соответствует выходной набор 3. Это означает, что в данной строке в столбцах 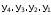проставляется код 0011, соответствующий числу 3; входному набору 1 соответствует выходной набор 5 - 0101 и т.д. Входные наборы {6, 7} не подаются, поэтому в строках, соответствующих этим наборам на пересечении со столбцами 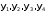, проставляется знак "
", означающий безразличное состояние (0 или I). В дальнейшем, на этапе минимизации целесообразно учитывать безразличные состояния, что позволяет получить более простые функции.
Составим по ТИ переключательные (выходные) функции схемы.
Функции выходов могут быть вычислены как по разрешенным наборам (в виде СДНФ), так и по запрещенным наборам (в виде СКНФ). Запишем выходные функции в виде СДНФ.
Произведем минимизацию функций по картам Карно. Особенностью минимизации является наличие в таблице истинности безразличных состояний. Ввиду недостижимости этих состояний при нормальной работе схемы им можно поставить в соответствие любое значение: либо 0, либо I. Для получения более простой функции целесообразно безразличным состояниям задавать такие значения, при которых в карте Карно получаются контуры с максимально возможным числом клеток.
Для примера имеем следующие карты Карно (рис.2). В карте функции 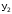клетка, соответствующая набору 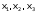, включена в контур с разрешенными наборами, следовательно, и на наборе 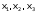функция .
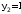Вид карты Карно для четырех и пяти переменных показан на рис.3.
Рис.2. Карты Карно для трех переменных
Рис.3. Карты Карно для четырех и пяти переменных
Реализация полученных функций преобразователя кодов производится в указанном преподавателем элементном базисе. В связи с этим реальная схема дискретного устройства должна быть пересчитана и составлена на заданный тип элементов. Реализацию следует производить в виде единой схемы, имеющей общие элементы для разных функций (см. рис. 4).
В данной лабораторной работе этот этап синтеза практически не рассматривается, а производится только сборка синтезированной схемы в поле программы Proteus 7.0. и её испытание.
Рис.4. Схема преобразователя кодов
Для подключения цифровых, например, семисегментных свето-диодных индикаторов, требуется специальный преобразователь (рис.5) двоичного кода на все сочетания в код этого индикатора (к ним относятся, например, ИМС 7447 и 7448 из серии TTL74 – аналоги отечественных ИМС 514ИД1 и 514ИД2), когда число светящихся сегментов может быть от двух (для цифры 1) до семи (для цифры 8). Поскольку число входов преобразователя равно четырем (для кодирования десятичных чисел 0-9 достаточно иметь 4-х разрядный двоичный код), а число выходов равно семи (по числу сегментов), то таблица истинности этого преобразователя содержит 11 столбцов и 10 строк (число десятичных цифр). Система переключательных функций, описывающих схему преобразователя будет содержать семь уравнений.
Из рис.5 следует, что, например, в цифре 0 должны светиться все сегменты, кроме сегмента G. Студентам предлагается самим построить ТИ данного преобразователя кодов, составить по ТИ переключательные (выходные) функции схемы, используя карты Карно для четырех переменных, произвести минимизацию полученных ПФ, собрать синтезированную схему преобразователя в поле программы Proteus 7.0. и провести её испытание.
Рис. 5. Преобразоватеь кода “4 в 7” и подключение индикатора
3. Описание рабочего места
Работа выполняется на компьютере, в программе Proteus 7.0 Сигналы логического «0» и «1» от аргументов Х задаются в ручном режиме. Графические изображения элементов с заданным числом входов, реализующих исследуемые функции, выбираются из окна библиотеки компонентов (подкатегория Modeling Primitives). При составлении схем соединение элементов производится вручную с помощью «мыши». Значения сигналов определяются через логический пробник или осциллограф, которые можно подключать к выходам исследуемой схемы.
4. Задание к лабораторной работе
1. Изучить основные этапы синтеза комбинационных схем.
2. Изучить основные этапы синтеза преобразователей кодов.
3.Провести синтез преобразователя кодов для варианта, указанного преподавателем.
4. Составить и собрать схему преобразователя кодов на компьютере в поле программы Proteus 7.0 и провести анализ её работы.
Варианты заданий
Задание 1. Произвести синтез преобразователя кода из двоичного в код "2 из 5".
Преобразователь имеет четыре входа: 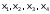, соответствующие разрядам двоичного кода, и пять выходов: 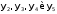, соответствующие разрядам кода "2 из 5".
Зависимость выходных комбинаций кода "2 из 3" от входных комбинаций двоичного кода представлена в табл.2.
Таблица 2
№
Вход преобразователя
Выход преобразователя
Запрещенные комби-нации
Двоичный код
Код “2 из 5”
Двоичный код
1
0,1,2,3,4,5,6,7,8,9
3,5,9,17,6,10,18,12,20,24
10,11,12,13,14
2
0,1,4,5,8,9,10,11,14,15
3,9,6,18,5,17,10,24,20,12
2,3,6,7,12,13
3
6,7,8,9,10,11,12,13,14,15
24,20,12,18,10,6,17,9,5,3
0,1,2,3,4,5
4
0,1,2,3,4,11,12,13,14,15
5,17,10,12,24,3,9,6,18,20
5,6,7,8,9,10
Предполагается, что неиспользуемые (запрещенные) комбинации двоичного кода на вход преобразователя не подаются и значение выходов при этом безразлично.
Задание 2. Произвести синтез преобразователя двоичного кода в код с проверкой на нечетность.
Преобразователь имеет четыре входа 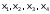, соответствующие разрядам двоичного кода, и пять выходов 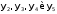, соответствующие разрядам кода с проверкой на нечетность. Предполагается, что запрещенные комбинации двоичного кода на вход преобразователя не подаются (табл.3).
Таблица 3
№
Вход преобразователя
Выход преобразователя
Запрещенные комбинации
Двоичный код
Код c проверкой на нечетность
Двоичный
код
1
0,1,2,3,4,5,6,7,8,9
16,1,2,19,4,21,22,7,8,25
10,11,12,13,14
2
0,1,4,5,8,9,10,11,14,15
22,7,8,25,26,11,28,13,14,31
2,3,6,7,12,13
3
6,7,8,9,10,11,12,13,14,15
16,1,21,9,4,11,28,13,14,31
0,1,2,3,4,5
4
0,1,2,3,4,11,12,13,14,15
16,1,4,21,8,25,28,13,14,31
5,6,7,8,9,10
Задание 3. Произвести синтез преобразователя двоичного кода в код для семисегментного светодиодного индикатора.
Преобразователь имеет четыре входа 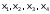, соответствующие разрядам двоичного кода, и семь выходов: 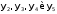, соответствующих количеству сегментов индикатора. Предполагается, что на вход преобразователя подаются только комбинации двоичного кода, соответствующие десятичным числам от 0 до 9.
Задание 4. Выбрать из библиотеки компонентов ИМС (серия TTL 74, подкатегория Decoders) по указанию преподавателя, один из преобразователей (7447, 7448 или 74247), исследовать его работу и составить таблицу истинности.
5. Указания к выполнению работы
1. Составить таблицу истинности преобразователя кодов по предложенному варианту (табл. 2 ÷ табл.4).
2. Составить по ТИ переключательные функции схемы в виде СДНФ.
3. Минимизировать полученные функции по картам Карно
4. По полученной минимизированной форме функции составить схему преобразователя.
5. Собрать составленную схему устройства в поле программы Proteus 7.0. Если рассматриваемая переменная входит в конъюнкцию со знаком инверсии, то сигнал на вход элемента И подаётся через инвертор.
6. Проанализировать работу схемы на соответствие заданной таблице истинности. Для этого, задавая значения входных сигналов аргументов 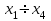при помощи логических имитаторов LOGIGSTATE, набрать по очереди все комбинации значений входных переменных и пользуясь логическими пробниками LOGICPROBE, многоканальным логическим анализатором LOGIC ANALIYSER или осциллографом, записать соответствующие значения выходов схемы.
6. Содержание отчёта
В отчете необходимо отразить: 1. Цель работы; 2. Заданную переключательную функцию в виде СДНФ; 3. Ход минимизации ПФ;
4.Полученную минимальную форму ПФ; 5. Схему минимизированной формы ПФ в заданном элементном базисе; 6. Результаты проверки схемы преобразователя (или ИМС) в виде таблицы истинности.
7. Контрольные вопросы
1. На каких законах алгебры логики основывается минимизация методом карт Карно?
2. Почему при минимизации безразличным состояниям в ТИ можно поставить в соответствие любое значение переменной – либо 0, либо 1?
3. Какие устройства называются трансляторами кодов?
4. Чему равно число столбцов таблицы истинности преобразователя двоичного кода на все сочетания в код “m из n”?
5. Почему преобразователь двоичного кода в код с проверкой на нечетность имеет четыре входа и пять выходов?
6. Какие устройства являются частными случаями преобразователей кодов?
ЛАБОРАТОРНАЯ РАБОТА № 13
Изучение различных преобразователей двоичных сигналов
1. Цель работы
Изучение способов построения преобразователей сигналов двоичного кода на все сочетания в специальные и помехозащищенные коды и обратно.
2. Общие сведения
Преобразователями кодов называются устройства, служащие для перевода n-элементного параллельного кода на входе в m-элементный параллельный код на выходе. На рис.1 представлено условное обозна-чение преобразователя кодов. Частным случаем преобразователей кодов являются шифраторы и дешифраторы. Преобразователи кодов, не являющиеся шифраторам или дешифраторам, называют трансляторами кодов или, собственно, преобразователями кодов.
Рис.1. Условное обозначение преобразователя кодов
Обычный подход к построению транслятора кодов основан на представлении его в виде комбинационного устройства с несколькими входами и выходами. Рассмотрим этот метод на примере преобразования двоичного кода на все сочетания в равновесный код “2 из 4” (код “m из n”).
Пусть на вход преобразователя поступают комбинации двоичного кода для десятичных чисел [О, I, 2, 3, 4, 5], которым соответствуют комбинации кода “2 из 4” для десятичных чисел [3, 5, 9, 6, 10, I2]. Тогда преобразователь имеет три входа Х1, Х2 и Х3, соответствующие разрядам двоичного кода, и четыре выхода: y1‚ y2, y3, и y4, соответствующие разрядам кода “2 из 4”. Предполагается, что неиспользованные комбинации двоичного кода чисел {6, 7} на вход преобразователя не подаются и значение выходов при этом безразлично. На основании задания для разработки дискретного устройства составим таблицу истинности ТИ (табл.1).
Таблица 1
№
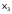
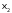
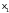
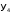
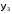
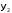
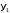
0
0
0
0
0
0
1
1
1
0
0
1
0
1
0
1
2
0
1
0
1
0
0
1
3
0
1
1
0
1
1
0
4
1
0
0
1
0
1
0
5
1
0
1
1
1
0
0
6
1
1
0
7
1
1
1
Таблица истинности имеет число столбцов, равное сумме входов и выходов и 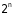строк, где n-число входов. Каждая строка таблицы истинности соответствует одному из входных наборов, причем десятичному номеру строки соответствует двоичный набор входных переменных.
По условию задачи входному набору 0 соответствует выходной набор 3. Это означает, что в данной строке в столбцах 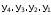проставляется код 0011, соответствующий числу 3; входному набору 1 соответствует выходной набор 5 - 0101 и т.д. Входные наборы {6, 7} не подаются, поэтому в строках, соответствующих этим наборам на пересечении со столбцами 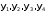, проставляется знак "
", означающий безразличное состояние (0 или I). В дальнейшем, на этапе минимизации целесообразно учитывать безразличные состояния, что позволяет получить более простые функции.| № | | | | | | | |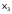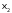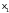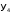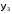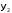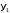
| 0 | 0 | 0 | 0 | 0 | 0 | 1 | 1 |
| 1 | 0 | 0 | 1 | 0 | 1 | 0 | 1 |
| 2 | 0 | 1 | 0 | 1 | 0 | 0 | 1 |
| 3 | 0 | 1 | 1 | 0 | 1 | 1 | 0 |
| 4 | 1 | 0 | 0 | 1 | 0 | 1 | 0 |
| 5 | 1 | 0 | 1 | 1 | 1 | 0 | 0 |
| 6 | 1 | 1 | 0 | | | | |
| 7 | 1 | 1 | 1 | | | | |
Составим по ТИ переключательные (выходные) функции схемы.
Функции выходов могут быть вычислены как по разрешенным наборам (в виде СДНФ), так и по запрещенным наборам (в виде СКНФ). Запишем выходные функции в виде СДНФ.
Произведем минимизацию функций по картам Карно. Особенностью минимизации является наличие в таблице истинности безразличных состояний. Ввиду недостижимости этих состояний при нормальной работе схемы им можно поставить в соответствие любое значение: либо 0, либо I. Для получения более простой функции целесообразно безразличным состояниям задавать такие значения, при которых в карте Карно получаются контуры с максимально возможным числом клеток.
Для примера имеем следующие карты Карно (рис.2). В карте функции
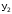клетка, соответствующая набору 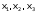, включена в контур с разрешенными наборами, следовательно, и на наборе 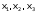функция 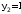. Вид карты Карно для четырех и пяти переменных показан на рис.3.
Рис.2. Карты Карно для трех переменных
Рис.3. Карты Карно для четырех и пяти переменных
Реализация полученных функций преобразователя кодов производится в указанном преподавателем элементном базисе. В связи с этим реальная схема дискретного устройства должна быть пересчитана и составлена на заданный тип элементов. Реализацию следует производить в виде единой схемы, имеющей общие элементы для разных функций (см. рис. 4).
В данной лабораторной работе этот этап синтеза практически не рассматривается, а производится только сборка синтезированной схемы в поле программы Proteus 7.0. и её испытание.
Рис.4. Схема преобразователя кодов
Для подключения цифровых, например, семисегментных свето-диодных индикаторов, требуется специальный преобразователь (рис.5) двоичного кода на все сочетания в код этого индикатора (к ним относятся, например, ИМС 7447 и 7448 из серии TTL74 – аналоги отечественных ИМС 514ИД1 и 514ИД2), когда число светящихся сегментов может быть от двух (для цифры 1) до семи (для цифры 8). Поскольку число входов преобразователя равно четырем (для кодирования десятичных чисел 0-9 достаточно иметь 4-х разрядный двоичный код), а число выходов равно семи (по числу сегментов), то таблица истинности этого преобразователя содержит 11 столбцов и 10 строк (число десятичных цифр). Система переключательных функций, описывающих схему преобразователя будет содержать семь уравнений.
Из рис.5 следует, что, например, в цифре 0 должны светиться все сегменты, кроме сегмента G. Студентам предлагается самим построить ТИ данного преобразователя кодов, составить по ТИ переключательные (выходные) функции схемы, используя карты Карно для четырех переменных, произвести минимизацию полученных ПФ, собрать синтезированную схему преобразователя в поле программы Proteus 7.0. и провести её испытание.
Рис. 5. Преобразоватеь кода “4 в 7” и подключение индикатора
3. Описание рабочего места
Работа выполняется на компьютере, в программе Proteus 7.0 Сигналы логического «0» и «1» от аргументов Х задаются в ручном режиме. Графические изображения элементов с заданным числом входов, реализующих исследуемые функции, выбираются из окна библиотеки компонентов (подкатегория Modeling Primitives). При составлении схем соединение элементов производится вручную с помощью «мыши». Значения сигналов определяются через логический пробник или осциллограф, которые можно подключать к выходам исследуемой схемы.
4. Задание к лабораторной работе
1. Изучить основные этапы синтеза комбинационных схем.
2. Изучить основные этапы синтеза преобразователей кодов.
3.Провести синтез преобразователя кодов для варианта, указанного преподавателем.
4. Составить и собрать схему преобразователя кодов на компьютере в поле программы Proteus 7.0 и провести анализ её работы.
Варианты заданий
Задание 1. Произвести синтез преобразователя кода из двоичного в код "2 из 5".
Преобразователь имеет четыре входа:
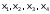, соответствующие разрядам двоичного кода, и пять выходов: 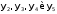, соответствующие разрядам кода "2 из 5".Зависимость выходных комбинаций кода "2 из 3" от входных комбинаций двоичного кода представлена в табл.2.
Таблица 2
| № | Вход преобразователя | Выход преобразователя | Запрещенные комби-нации |
| Двоичный код | Код “2 из 5” | Двоичный код | |
| 1 | 0,1,2,3,4,5,6,7,8,9 | 3,5,9,17,6,10,18,12,20,24 | 10,11,12,13,14 |
| 2 | 0,1,4,5,8,9,10,11,14,15 | 3,9,6,18,5,17,10,24,20,12 | 2,3,6,7,12,13 |
| 3 | 6,7,8,9,10,11,12,13,14,15 | 24,20,12,18,10,6,17,9,5,3 | 0,1,2,3,4,5 |
| 4 | 0,1,2,3,4,11,12,13,14,15 | 5,17,10,12,24,3,9,6,18,20 | 5,6,7,8,9,10 |
Предполагается, что неиспользуемые (запрещенные) комбинации двоичного кода на вход преобразователя не подаются и значение выходов при этом безразлично.
Задание 2. Произвести синтез преобразователя двоичного кода в код с проверкой на нечетность.
Преобразователь имеет четыре входа
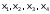, соответствующие разрядам двоичного кода, и пять выходов 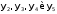, соответствующие разрядам кода с проверкой на нечетность. Предполагается, что запрещенные комбинации двоичного кода на вход преобразователя не подаются (табл.3).Таблица 3
| № | Вход преобразователя | Выход преобразователя | Запрещенные комбинации |
| Двоичный код | Код c проверкой на нечетность | Двоичный код | |
| 1 | 0,1,2,3,4,5,6,7,8,9 | 16,1,2,19,4,21,22,7,8,25 | 10,11,12,13,14 |
| 2 | 0,1,4,5,8,9,10,11,14,15 | 22,7,8,25,26,11,28,13,14,31 | 2,3,6,7,12,13 |
| 3 | 6,7,8,9,10,11,12,13,14,15 | 16,1,21,9,4,11,28,13,14,31 | 0,1,2,3,4,5 |
| 4 | 0,1,2,3,4,11,12,13,14,15 | 16,1,4,21,8,25,28,13,14,31 | 5,6,7,8,9,10 |
Задание 3. Произвести синтез преобразователя двоичного кода в код для семисегментного светодиодного индикатора.
Преобразователь имеет четыре входа
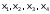, соответствующие разрядам двоичного кода, и семь выходов: 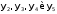, соответствующих количеству сегментов индикатора. Предполагается, что на вход преобразователя подаются только комбинации двоичного кода, соответствующие десятичным числам от 0 до 9.Задание 4. Выбрать из библиотеки компонентов ИМС (серия TTL 74, подкатегория Decoders) по указанию преподавателя, один из преобразователей (7447, 7448 или 74247), исследовать его работу и составить таблицу истинности.
5. Указания к выполнению работы
1. Составить таблицу истинности преобразователя кодов по предложенному варианту (табл. 2 ÷ табл.4).
2. Составить по ТИ переключательные функции схемы в виде СДНФ.
3. Минимизировать полученные функции по картам Карно
4. По полученной минимизированной форме функции составить схему преобразователя.
5. Собрать составленную схему устройства в поле программы Proteus 7.0. Если рассматриваемая переменная входит в конъюнкцию со знаком инверсии, то сигнал на вход элемента И подаётся через инвертор.
6. Проанализировать работу схемы на соответствие заданной таблице истинности. Для этого, задавая значения входных сигналов аргументов
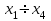при помощи логических имитаторов LOGIGSTATE, набрать по очереди все комбинации значений входных переменных и пользуясь логическими пробниками LOGICPROBE, многоканальным логическим анализатором LOGIC ANALIYSER или осциллографом, записать соответствующие значения выходов схемы. 6. Содержание отчёта
В отчете необходимо отразить: 1. Цель работы; 2. Заданную переключательную функцию в виде СДНФ; 3. Ход минимизации ПФ;
4.Полученную минимальную форму ПФ; 5. Схему минимизированной формы ПФ в заданном элементном базисе; 6. Результаты проверки схемы преобразователя (или ИМС) в виде таблицы истинности.
7. Контрольные вопросы
1. На каких законах алгебры логики основывается минимизация методом карт Карно?
2. Почему при минимизации безразличным состояниям в ТИ можно поставить в соответствие любое значение переменной – либо 0, либо 1?
3. Какие устройства называются трансляторами кодов?
4. Чему равно число столбцов таблицы истинности преобразователя двоичного кода на все сочетания в код “m из n”?
5. Почему преобразователь двоичного кода в код с проверкой на нечетность имеет четыре входа и пять выходов?
6. Какие устройства являются частными случаями преобразователей кодов?