Файл: 1 статистический анализ случайных величин статистический анализ одномерной последовательности случайных величин Цель работы.docx

Тогда дисперсия для группированного ряда определится так:D = ______________________________________________.Среднее квадратическое отклонение группированного ряда.Среднее квадратическое отклонение – (дать определение).Среднее квадратическое отклонение рассчитывается по формуле:σ = 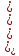,где ?????Для заданных исходных данных получим:σ = ______ = _______.Коэффициент вариации группированного рядаКоэффициент вариации – (дать определение).Коэффициент вариации определяется по формуле:δ =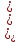где ??????.Для заданных исходных данных получим:δ = ________= ______.Средствами программы Excel рассчитаны характеристики описательной статистики группированного ряда (в качестве исходных данных необходимо применять данные таблицы 1.3), числовые значения которых приведены на рисунке 1.6.Рисунок 1.6 – Характеристики описательной статистикиВывод. (приводится сравнение расчетных значений, выполненных вручную и выполненной с помощью ПК)________________________________________________________

2. 
   Интервальный статистический ряд
   

Интервальный ряд – (дать определение) . Для построения интервального ряда примем количество интерваловt = ______ Ширина интервалов определяется по формуле:r_t =__________,где - ??????. При заданных исходных данных получим:r_t= ___________.В таблице 1.6 показаны значения границ интервалов и средние значения величин кажого интервала . Таблица 1.6 – Значения границ интервалов

Номер интервала, t	Значение левой границе интервала	Значение правой границе интервала	Среднее значение случайной величины в интервале
1
2
3
4
5
6
7
8
9
10

---

Интервальный ряд представлен в таблице 1.7.Таблица 1.7 - Интервальный ряд

Номер интервала	Среднее значение xi	Частоты попадания в интервал	Накопленная частота
1
2
3
4
5
6
7
8
9
10

Графическое представление статистических характеристик рядаГистограмма интервального ряда.Гистограмма по средним значениям интервального ряда показана на рисунке 1.7.Полигон интервального ряда.Полигон для интервального ряда показан на рис. 1.8Кумулята интервального ряда.Кумулята для интервального ряда показан на рисунке 1.9.Огива интервального ряда.Огива для интервального ряда показана на рисунке 1.10.Рисунок 1.7 - Гистограмма для интервального рядаРисунок 1.8 – Полигон для интервального рядаРисунок 1.9 – Кумулята для группированного ряда

---

Рисунок 1.10 – Огива для интервального ряда Статистические характеристики интервального ряда.Объем выборки интервального ряда.При заданных значениях интервального ряда получим объём выборки:N= ___________________________.= _________,Относительная частота интервального ряда.Для первого значения интервального ряда получим:W = ___________________________.= _________,Значения относительных частот приведены в таблице 1.8. Таблица 1.8- Относительные частоты для группированного ряда

Частота	Сумма n	Относительная частота W	Сумма относительной частоты

Среднее арифметическое интервального ряда.Для заданных исходных данных получим:X_ср= __________________________ = ___________,Средневзвешенное интервального ряда.Для заданных исходных данных получим:X_св = ______________________ = _____,Мода интервального ряда.Мода для интервального ряда и для заданного ряда случайных величин имеет значение:M = __________.Медиана интервального ряда.Медиана для интервального ряда имеет значение:Me = ______ = ______.Дисперсия интервального ряда.Расчетные значения дисперсии для группированного ряда приведены в таблице 1.9.Таблица 1.9 – Расчет дисперсии ряда

Номер интервала	Среднее значение xt	Частоты ni	Среднее арифметическое	(xi-xср.ар)2*nt	1/(n-1)
1
2
3
4
5
6
7
8
9
10

---

Тогда дисперсия для интервального ряда примет значение:D = ____________________________________.Среднее квадратическое отклонение интервального рядаДля заданных исходных данных получим:σ = ______ = _______.Коэффициент вариации интервального рядаДля заданных исходных данных получим:δ = ________= ______.Характеристики описательной статистики интервального ряда.Средствами программы Excel рассчитаны характеристики описательной статистики заданного ряда (для корректного расчета данных характеристик необходимо построить полный интервальный ряд для средних значений случайной величины в табл. 1.10).Таблица 1. 10- Полный интервальный ряд

Численные средние значения интервального ряда

Числовые значения, рассчитанные в программе Excel, приведены на рисунке 1.11.Рисунок 1.11 – Характеристики описательной статистикиВывод. (аналогично разделу 3.1)________________________________________________________

---

2.1 Статистический анализ двумерной последовательности случайных величин

Цель работы. Освоить компетенции выполнения статистического анализа двумерных данных, выявить зависимость (связь) между случайными величинами.

2.1.1 Исходные данныеВ качестве исходных данных принято двух последовательных случайных величин : первая – (дать название)_____________________________________;вторая - (дать название)_____________________________________.Исходные данные представлены в таблице 2.1. Таблица 2.1 – Исходные данные

Название (обозначение) 1 случайной величины	Название (обозначение) 2 случайной величины 2		Название (обозначение) 1 случайной величины	Название (обозначение) 2 случайной величины

---