Файл: 1 статистический анализ случайных величин статистический анализ одномерной последовательности случайных величин Цель работы.docx

Экспериментальные значения целевой функции.

Номер опыта	Y1	Y2	Y3	Y4	Y5
1
2
3
4
5
6
7
8

Расчет среднего арифметического результатов каждого опыта.

Номер опыта	Y1	Y2	Y3	Y4	Y5	Yср
1
2
3
4
5
6
7
8

---

Дисперсия среднего арифметического для каждой строки матрицы эксперимента (каждого опыта).

Дисперсия среднего арифметического определяется формулой:


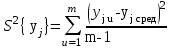
где ?????.

Номер опыта	Y1	Y2	Y3	Y4	Y5	Yср	S2y
1
2
3
4
5
6
7
8

Оценка однородности построчных дисперсий.

Расчетное значение критерия Кохрена.

Критерий Кохрена показывает, какую долю в общей сумме построчных дисперсий занимает максимальная из них, и определяется по формуле:



где ?????.
Максимальное значение дисперсии результатов опыта:

---

S²_ymax= __________ = __________.
Сумма всех построчных дисперсий:
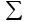S² _y = ________________________________________________ = _____.
Расчетное значение критерия Кохрена:
Gp= _______.
В случае идеальной однородности построчных дисперсий коэффициент Gp стремился бы к значению 1/N , где N – число опытов (количество строк в матрице планирования).

Табличное значение критерия Кохрена.

Уровень значимости.
 = ______.
Степень числителя (f₁):
f1= m –1= ________,
где m – количество параллельных опытов в строке матриц
Степень свободы знаменателя (f2):
f2 = N = ______,
где N – общее число опытов в матрице.
Табличное значение критерия Кохрена
Gт = _________.
Вывод ________________________________________________________
Вид уравнения регрессии, принятого для построения модели функции отклика.

Рекомендуется полиномиальная модель функции отклика
y = ______________________________________________________.
Коэффициенты регрессии.

Значения коэффициентов регрессии определяются по формулам:

;

и так далее для всех коэффициентов.
Таблица - Значения коэффициентов регрессии.

b0	b1	b2	b3	b12	b23	b13	b123

Статистическая значимость коэффициентов регрессии.

---

Расчетные значения критерия Стьюдента.

Оценка производится по t-критерию Стьюдента. Проверяется отклонение от нуля найденной оценки.

Для каждого коэффициента b_k вычисляется расчетное значение критерия Стьюдента:

;

;

;

,

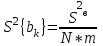где b_k – коэффициент уравнения регрессии;

S{b_k} – оценку дисперсию коэффициентов, найденных по экспериментальным данным;

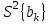- дисперсия коэффициентов, найденных по экспериментальным данным;

- дисперсия воспроизводимости.
S²_b = _______________________________________ = _____________.
S²_{bk} = ___________________ = ______________.
S{bk} = ____________________.
Расчетные значения критерия Стьюдента

t0	t1	t2	t3	t12	t23	t13	t123

Табличные значения критерия Стьюдента.

Уровень статистической значимости.
 = ______________.
Степень свободы
f = _____________.
Функция отклика со статистически значимыми коэффициентами.

Функция отклика со статистически значимыми коэффициентами имеет вид:
y = __________________________
Значения функции отклика для каждого опыта по новой функции отклика со статистически значимыми коэффициентами.

Номер опыта	Y’
1
5
7
3
6
2
4
8

---

Проверка адекватности новой функции отклика со статистически значимыми коэффициентами.

Расчетное значение критерия Фишера (F- критерия).

Адекватность модели проверяют по критерию Фишера , расчетное значение которого определяется по формуле:

F_p= S²_ад/S²_в ;
;

,

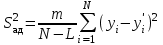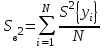где ????
S²_ад = ______________ = _________;
S²_в = _______________ = _________;
F_p = _______________ = __________.
Уровень значимости  = ___________.
Степень свободы адекватности:
f_ад = ___________ = ______.
Степень свободы воспроизводимости:
f_в = ___________ = _______.
Табличное значение критерия Фишера.
F_т = ________.
Вывод ________________________________________________________
Функция отклика со статистически значимыми коэффициентами и натуральными факторами.

Функция отклика со статистически значимыми коэффициентами и натуральными факторами имеет вид:
y = ___________.
Заключение _________________________________________________________

Литература

1. 
   Сидняев Н.И. Теория планирования эксперимента и анализ статистических данных: учебн. пособ. / Н.И. Сидняев. – М.: Изд-во Юрайт, 2011.- 399 с.
   

1. 
   2.Гмурман В.Е. Теория вероятностей и математическая статистика: учеб.пособ.-12-е изд., перераб. / В.Е. Гмурман.- М.: Изд-во Юрайт, 2010.- 479 с.
   
2. 
   Гмурман В.Е. Руководство к решению задач по теории вероятностей и математической статистике: Учебн. пособ. -12-е изд., перераб. / В.Е. Гмурман. – М.: Высшобраз.,2006. – 476 с.
   
3. 
   Боровков, А.А. Математическая статистика: Учебник / А. А. Боровков. – Изд. 4-е, стер. – Санкт-Петербург; М.; Краснодар: Лань, 2010. – 703 с. (электронный ресурс).
   
4. 
   Адлер Ю.П., Маркова Е.В., Грановский Ю.В. Планирование эксперимента при поиске оптимальных условий. М.: Наука, 1976.
   
5. 
   Асатурян В.И. Теория планирования эксперимента: Учеб. пособие для втузов. М.: Радио и связь, 1983.
   
6. 
   Налимов В.В. Теория эксперимента. М.: Наука, 1971.
   
7. 
   Планирование и организация измерительного эксперимента / Е.Т. Володаpский, Б.Н. Малиновский, Ю.М. Туз.-К.: В.ш. Головное изд-во, 1987.
   

---