Файл: Лабораторная работа показатели надежности восстанавливаемого объекта.docx
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 11.01.2024
Просмотров: 62
Скачиваний: 1
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
ЛАБОРАТОРНАЯ РАБОТА 5.
Показатели надежности восстанавливаемого объекта
Цель: приобретение навыков расчета показателей надежности восстанавливаемого объекта.
Задачи:
-
ознакомиться с показателями восстанавливаемого объекта.
Основные теоретические сведения
Восстанавливаемыйобъект – это объект, для которого в рассматриваемой ситуации проведение восстановления работоспособного состояния предусмотрено в научно-технической и (или) конструкторской документации.
Средняя наработка на отказ
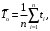 (1)
(1)где ti – наработка между i-1 и i-м отказами, ч;
n(t) – суммарное число отказов за время t.
Среднее время восстановления
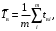 (2)
(2)m– число отказов, последствия которых устранены;
tвi – время восстановления работоспособного состояния после i-го отказа.
Коэффициент готовности
Вероятность того, что изделие будет работоспособно в произвольный момент времени, кроме периодов, когда применение изделия по назначению исключено
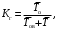 (3)
(3)где
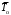 – средняя наработка на отказ;
– средняя наработка на отказ;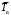 – среднее время восстановления.
– среднее время восстановления.Коэффициент технического использования
Характеризует долю времени нахождения элемента в работоспособном состоянии относительно рассматриваемой продолжительности эксплуатации
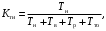 (4)
(4)где Tн– суммарная наработка изделия в рассматриваемый промежуток времени;
Tв, Tpи Tто– суммарное время, затраченное на восстановление, ремонт и ТО изделия за тот же период.
Примеры решения задач
Пример 1. В течение некоторого периода времени производилось наблюдение за работой одного объекта. За весь период зарегистрировано
n=15 отказов. До начала наблюдений объект проработал 258 ч, к концу наблюдения наработка составила 1233 ч. Определить среднюю наработку на отказ
 .
.Решение
Наработка за указанный период составила
∆t=t2–t1=1233–258=975 ч.
Наработка на отказ по статистическим данным (1)
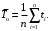
Приняв
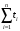 = 975 ч, определим среднюю наработку на отказ
= 975 ч, определим среднюю наработку на отказ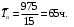
Пример 2. В аппаратуре было зафиксировано 8 отказов. Время восстановления составило: t1 = 12 мин, t2 = 23 мин, t3 = 15 мин, t4= 9 мин, t5= 17 мин, t6 = 28 мин, t7 = 25 мин, t8 = 31 мин. Определить среднее время восстановления аппаратуры
 .
.Решение
Среднее время восстановления аппаратуры (2)
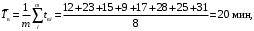
Пример 3. Система состоит из 5 приборов. Отказ каждого прибора ведет к отказу системы. Известно, что первый отказал 34 раза в течение 952 ч работы, второй – 24 раза в течение 960 ч работы, а остальные приборы в течение 210 ч работы отказали 4, 6 и 5 раз соответственно. Требуется определить наработку на отказ системы в целом, если справедлив экспоненциальный закон надежности1 для каждого из пяти приборов, среднее число исправно работающих изделий в интервале ∆tравно пяти. Построить функцию надежности P(t) и функцию распределения отказов Q(t)2. Определить вероятность безотказной работы при t=100 ч.
Решение
Суммарная интенсивность отказов системы:
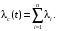
Определим интенсивность отказов для каждого прибора:
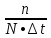
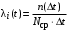 ,
,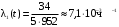 ,
, 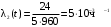 ,
, 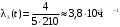
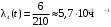 ,
, 
.
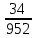
Интенсивность отказов системы будет
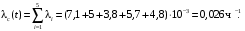
Средняя наработка на отказ системы равна
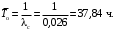
Для экспоненциального закона
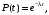
Следовательно
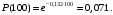
Пример 4. Аппаратура имела среднюю наработку на отказ
 =65 ч и среднее время восстановления
=65 ч и среднее время восстановления  =20 мин. Определить коэффициент готовности Кг.
=20 мин. Определить коэффициент готовности Кг.Решение
Коэффициент готовности (3)
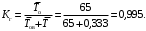
Пример 5. Известно, что интенсивность отказов λ=0,026 ч–1, а среднее время восстановления
 =20 мин. Требуется вычислить коэффициент готовности и функцию готовности изделия. Закон распределения экспоненциальный.
=20 мин. Требуется вычислить коэффициент готовности и функцию готовности изделия. Закон распределения экспоненциальный.Решение
Коэффициент готовности
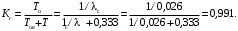
Пример 6. Определить коэффициент технического использования машины, если известно, что машину эксплуатируют в течение года Тэ=8760 ч. За этот период эксплуатации машины суммарное время восстановления отказов составило Tв=40 ч. Время проведения регламента ТО составляет Tто=20 ч. Суммарное время, затраченное на ремонтные работы за период эксплуатации, составляет 15 суток (Тр =15·24=360 ч).
Решение
Определим суммарное время наработки машины:
Tн=Тэ – (Tв+Tр+Tто)=8760 – (40+360+20)=8340.
Определим коэффициент технического использования (4)
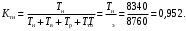
Пример 7. При эксплуатации сложной технической системы получены статистические данные по среднему времени наработки на отказ элементов tо и времения восстановления одного элемента, которые сведены в таблицу (табл. 1). Определить коэффициент готовности системы.
Таблица 1
Статистические данные
| Номер элемента | Число отказов ni | Число устраненных отказов тi | Время, ч | |
| tвi | tо | |||
| | 2 | 2 | 1 | 200 |
| | 5 | 5 | 2 | 300 |
| | 6 | 6 | 4 | 400 |
| | 4 | 4 | 3 | 300 |
| | 8 | 8 | 2 | 600 |
| | 10 | 10 | 5 | 700 |
| Итого | 35 | 35 | 17 | 2500 |
Наработка на отказ (1)
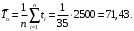
Среднее время восстановления (2)
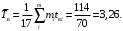
Коэффициент готовности изделия определяется по формуле (3).
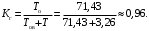
Задание
Задача 1. В течение некоторого периода времени производилось наблюдение за работой одного объекта. За весь период зарегистрированоn=10 отказов. До начала наблюдений объект проработал 258 ч, к концу наблюдения наработка составила 1000 ч. Определить среднюю наработку на отказ
 .
.Задача 2. В аппаратуре было зафиксировано 8 отказов. Время восстановления составило: t1=10 мин, t2=20 мин, t3=16 мин, t4=10 мин, t5=10 мин, t6=24 мин, t7=24 мин, t8=30 мин. Определить среднее время восстановления аппаратуры
 .
.Задача 3. Система состоит из 5 приборов. Отказ каждого прибора ведет к отказу системы. Известно, что первый отказал 30 раза в течение 950 ч работы, второй – 20 раз в течение 1000 ч работы, а остальные приборы в течение 210 ч работы отказали 3, 2 и 5 раз соответственно. Требуется определить наработку на отказ системы
 в целом, если справедлив экспоненциальный закон надежности для каждого из пяти приборов, среднее число исправно работающих изделий в интервале ∆tравно пяти. Определить вероятность безотказной работы при t=100 ч.
в целом, если справедлив экспоненциальный закон надежности для каждого из пяти приборов, среднее число исправно работающих изделий в интервале ∆tравно пяти. Определить вероятность безотказной работы при t=100 ч.Задача 4. Аппаратура имела среднюю наработку на отказ
 =74,2 ч и среднее время восстановления
=74,2 ч и среднее время восстановления  =18 мин. Требуется определить коэффициент готовности Кг.
=18 мин. Требуется определить коэффициент готовности Кг.Задача 5. Известно, что интенсивность отказов λ= 0,02 ч–1, а среднее время восстановления
 =18 мин. Требуется вычислить коэффициент готовности. Закон распределения экспоненциальный.
=18 мин. Требуется вычислить коэффициент готовности. Закон распределения экспоненциальный.Задача 6. Определить коэффициент технического использования машины, если известно, что машину эксплуатируют в течение года Тэ=9010 ч. За этот период эксплуатации машины суммарное время восстановления отказов составило Tв=50 ч. Время проведения регламента составляет
Tто=10 ч. Суммарное времяTр, затраченное на ремонтные работы за период эксплуатации составляет 10 суток.
Задача 7. При эксплуатации сложной технической системы получены статистические данные, которые сведены в таблицу (2). Определить коэффициент готовности системы.
Таблица 2
Статистические данные
| Номер элемента | Число устраненных отказов тi | Число отказов ni | Время, ч | |
| tв | tо | |||
| | 2 | 2 | 1 | 100 |
| | 5 | 5 | 2 | 200 |
| | 5 | 2 | 3 | 300 |
| | 4 | 4 | 2 | 100 |
| | 6 | 4 | 1 | 500 |
| | 6 | 4 | 1 | 500 |
Вопросы
-
Обоснуйте актуальность рассмотрения вопросов надежности ТС. Почему данные вопросы важны особенно важны для РФ? -
Поясните почему неисправное состояние может быть работоспособным. -
При обозначении заданного момента времени τ выберите правильную форму записи:
-
вероятность безотказной работы – Р(t<τ) или Р(t>τ); -
вероятность отказа – Q(t<τ) или Q(t>τ).
-
Поясните необходимость определения (по возможности) закона распределения вероятности отказа. -
Нарисуйте принятую для большинства сложных ТС кривую интенсивности отказов. Поясните ее вид.
1 - функция плотности распределения –
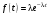 ;
;- функция распределения вероятности отказов –
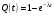 ;
;- математическое ожидание –
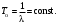
2
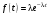
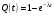
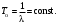 при выполнении на компьютере
при выполнении на компьютере