Файл: Баранова Олеся Александровна Учитель Бондарь Галина Владимировна Оглавление Введение Основная часть Теоретические сведения Мои исследования Собственное решение.doc
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 11.01.2024
Просмотров: 67
Скачиваний: 1
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
Трисектрисой угла называется каждый из двух лучей, делящих этот угол на три равные части.
Теорема Морли. Точки пересечения смежных трисектрис углов произвольного треугольника являются вершинами равностороннего (правильного) треугольника.
Доказательство. Нужно доказать, что треугольник XYZ - равносторонний.
Обратиться к приложению – рисунок 8.
Используя обозначения, приведённые в рисунке, поскольку в трeугольнике ABC сумма углов 3 α + 3 β + 3 γ =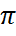
, имеем α + β + γ + 
Возьмём произвольный равносторонний треугольник XYZ. Пусть P, Q, R – точки на высотах треугольника ABC, такие что:
∟ XPY = ∟XPZ = α +
∟ YQZ = ∟YQX = β +
∟ZRX = ∟ZRY = γ +
Пусть A — точка пересечения QZ и RY, B — точка пересечения PX и PZ, и C — точка пересечения PY и QX. Тогда в четырехугольнике XRAQ:
∟AQX = 2 ß +
∟ARX = 2γ +
∟QXR = 2α + β + γ +
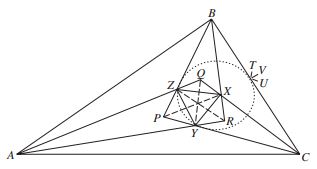
Обратиться к приложению – рисунок 9.
Следовательно, ∟ZAY = α .
Аналогично, ∟ XBZ = β и ∟YCX = γ .
Проведем окружность с центром в точке X, касающуюся PB. Так как PX — биссектриса ∟BPC, то эта окружность также касается PC. Теперь проведем касательные к окружности BT и CU. Обозначим через V точку пересечения этих касательных. Тогда
∟ XBT = ∟ XBZ = β и ∟XCU = ∟XCY = γ.
Тогда сумма углов P, B и C в четырехугольнике PBVC равна 2 α +
+ 2 β + 2 γ = 
,
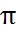Откуда ∟ TVU = 0 . Другими словами, BTUVC — прямая, так что точки T, U, и V совпадают. Следовательно, ∟ XBC = 3, ∟ XCB = γ . Аналогично определяются углы треугольников YCA и ZAB , откуда получаем, что углы треугольника ABC равны 3
α, 3 β и 3 γ . Если необходимо, этот треугольник можно заменить подобным ему, который будет совпадать с треугольником ABC.
4. Вывод
Несмотря на то, что уже тысячи лет великие умы человечества ищут способы осуществления трисекции угла с помощью циркуля и линейки, до сих пор решения не найдено. Это говорит о том, что она действительно не осуществима для большинства углов. Но всё равно находятся те, кто пытается предложить свой вариант решения, но впоследствии они опровергаются из-за какого-то маленького недочёта. Я оказалась в числе тех, кто остался не равнодушным к этой задачи и кто потратил своё время на поиск своего, уникального решения. Я не жалею, я однажды открыла для себя задачу о трисекции угла, ведь, благодаря процессу построения чертежей и выполнению доказательства, человек ищет какие-то алгоритмы, которые помогает ему мыслить логически. А без логики человеку в современном мире приходится очень тяжело. Я считаю, что каждому необходимо хотя бы пытаться находить различные способы решения одной и той же задачи, так как это развивает человека, заставляет его мыслить рационально. Надеюсь, что в следующей моей работе я представлю во внимание ещё более интересную неразрешимую или ещё не доказанную задачу, постараюсь в ней разобраться и найти какие-нибудь пути её разрешения
5. Список литературы
1. Архимед. Достижения в математике [Электронный ресурс]. – Режим доступа: http://www.univer.omsk.su/omsk/Edu/Math/aarhimed.htm
2. Архимед. Научная деятельность. Математика [Электронный ресурс]. – Режим доступа: http://ru.wikipedia.org/wiki/Архимед.
3. Архимедова спираль [Электронный ресурс]. – Режим доступа: http://ru.wikipedia.org/wiki/Архимедова_спираль.
4. Квадратриса. Кинематическое определение. Применение [Электронный ресурс]. – Режим доступа: http://ru.wikipedia.org/wiki/Квадратриса.
5. Квадратура круга [Текст]: история одной головоломки. // Занимательные головоломки. – 2012. - №3 (3 марта). – С. 13-14. 6. Конхоида Никомеда [Электронный ресурс]. – Режим доступа: http://ru.wikipedia.org/wiki/Конхоида_Никомеда.
7. Невсис. Применение [Электронный ресурс]. – Режим доступа: http://ru.wikipedia.org/wiki/Невсис.
6. Приложение
Рисунок 1. Улитка Паскаля.
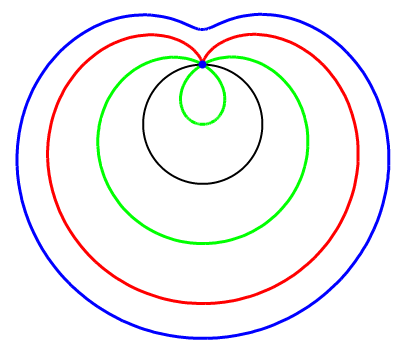
Три улитки паскаля, конхоиды чёрной окружности: зелёная a>l, красная (кардиоида) a=l и синяя a
В случае l=2a, улитка Паскаля также называется
трисектриса. Такое название она получила из-за того, что если на плоскости задана трисектриса, то трисекцию угла можно построить с помощью циркуля и линейки.
Рисунок 2. Квадратриса.
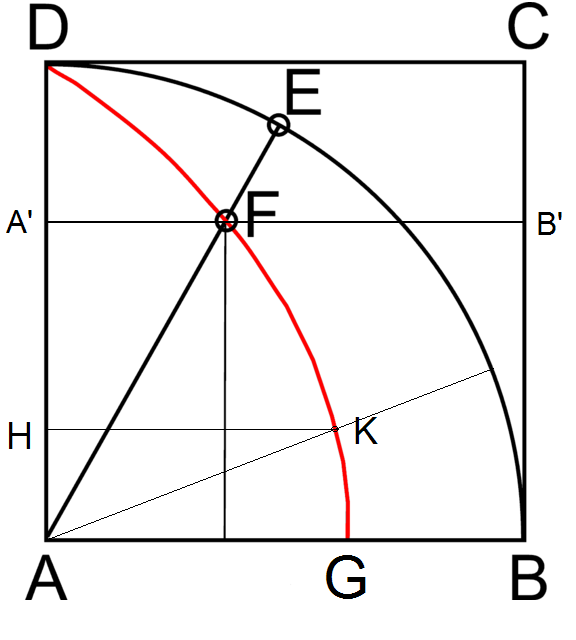
Рисунок 3. Конхоида Никомеда.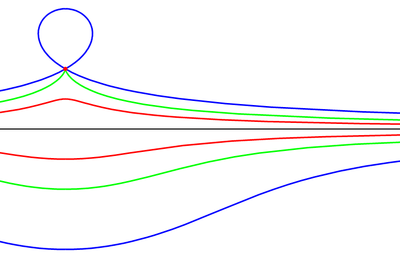
Три конхоиды прямой с общим центром.
Красная l = 2/а
Зелёная l = а
Синяя l = 2а
Рисунок 4. Архимедова спираль.
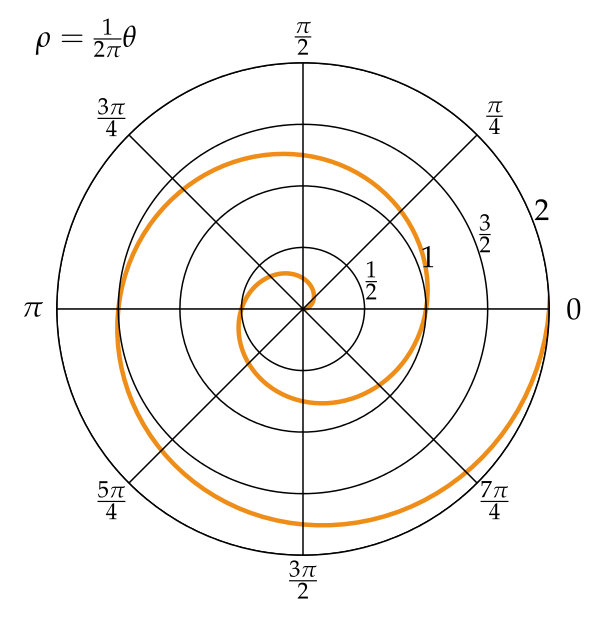
Рисунок 5. Невсис.
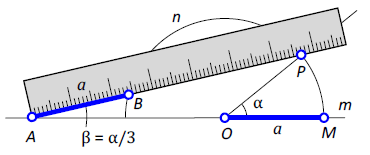
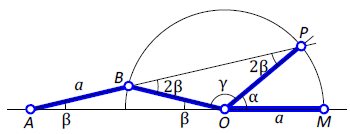
Рисунок 6. Папирофлексия.
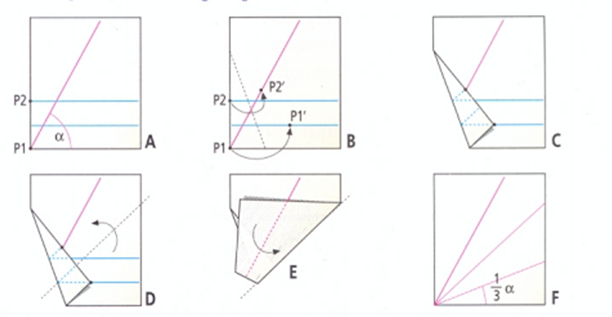
Рисунок 7. Чертёж к решению.
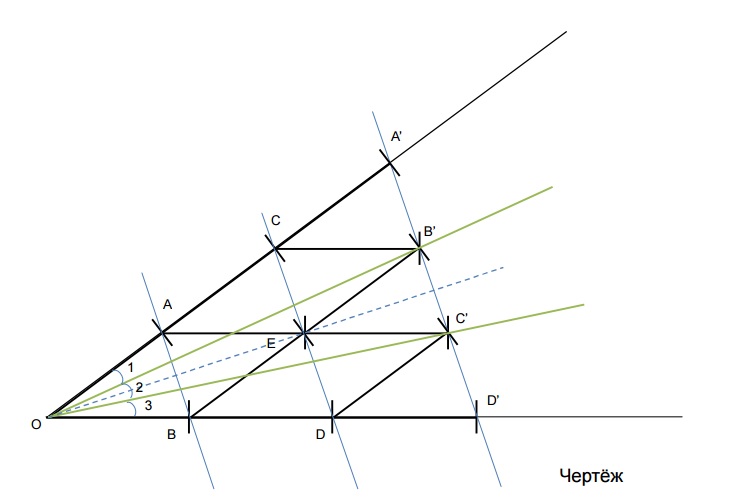
Рисунок 8. К Теореме Морлея.
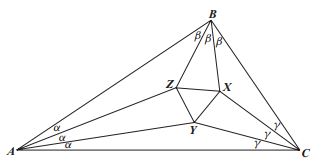
Рисунок 9. К теореме Морлея 2.
Теорема Морли. Точки пересечения смежных трисектрис углов произвольного треугольника являются вершинами равностороннего (правильного) треугольника.
Доказательство. Нужно доказать, что треугольник XYZ - равносторонний.
Обратиться к приложению – рисунок 8.
Используя обозначения, приведённые в рисунке, поскольку в трeугольнике ABC сумма углов 3 α + 3 β + 3 γ =
, имеем α + β + γ + Возьмём произвольный равносторонний треугольник XYZ. Пусть P, Q, R – точки на высотах треугольника ABC, такие что:
∟ XPY = ∟XPZ = α +
∟ YQZ = ∟YQX = β +
∟ZRX = ∟ZRY = γ +
Пусть A — точка пересечения QZ и RY, B — точка пересечения PX и PZ, и C — точка пересечения PY и QX. Тогда в четырехугольнике XRAQ:
∟AQX = 2 ß +
∟ARX = 2γ +
∟QXR = 2α + β + γ +
Обратиться к приложению – рисунок 9.
Следовательно, ∟ZAY = α .
Аналогично, ∟ XBZ = β и ∟YCX = γ .
Проведем окружность с центром в точке X, касающуюся PB. Так как PX — биссектриса ∟BPC, то эта окружность также касается PC. Теперь проведем касательные к окружности BT и CU. Обозначим через V точку пересечения этих касательных. Тогда
∟ XBT = ∟ XBZ = β и ∟XCU = ∟XCY = γ.
Тогда сумма углов P, B и C в четырехугольнике PBVC равна 2 α +
+ 2 β + 2 γ = ,Откуда ∟ TVU = 0 . Другими словами, BTUVC — прямая, так что точки T, U, и V совпадают. Следовательно, ∟ XBC = 3, ∟ XCB = γ . Аналогично определяются углы треугольников YCA и ZAB , откуда получаем, что углы треугольника ABC равны 3
α, 3 β и 3 γ . Если необходимо, этот треугольник можно заменить подобным ему, который будет совпадать с треугольником ABC.
4. Вывод
Несмотря на то, что уже тысячи лет великие умы человечества ищут способы осуществления трисекции угла с помощью циркуля и линейки, до сих пор решения не найдено. Это говорит о том, что она действительно не осуществима для большинства углов. Но всё равно находятся те, кто пытается предложить свой вариант решения, но впоследствии они опровергаются из-за какого-то маленького недочёта. Я оказалась в числе тех, кто остался не равнодушным к этой задачи и кто потратил своё время на поиск своего, уникального решения. Я не жалею, я однажды открыла для себя задачу о трисекции угла, ведь, благодаря процессу построения чертежей и выполнению доказательства, человек ищет какие-то алгоритмы, которые помогает ему мыслить логически. А без логики человеку в современном мире приходится очень тяжело. Я считаю, что каждому необходимо хотя бы пытаться находить различные способы решения одной и той же задачи, так как это развивает человека, заставляет его мыслить рационально. Надеюсь, что в следующей моей работе я представлю во внимание ещё более интересную неразрешимую или ещё не доказанную задачу, постараюсь в ней разобраться и найти какие-нибудь пути её разрешения
5. Список литературы
1. Архимед. Достижения в математике [Электронный ресурс]. – Режим доступа: http://www.univer.omsk.su/omsk/Edu/Math/aarhimed.htm
2. Архимед. Научная деятельность. Математика [Электронный ресурс]. – Режим доступа: http://ru.wikipedia.org/wiki/Архимед.
3. Архимедова спираль [Электронный ресурс]. – Режим доступа: http://ru.wikipedia.org/wiki/Архимедова_спираль.
4. Квадратриса. Кинематическое определение. Применение [Электронный ресурс]. – Режим доступа: http://ru.wikipedia.org/wiki/Квадратриса.
5. Квадратура круга [Текст]: история одной головоломки. // Занимательные головоломки. – 2012. - №3 (3 марта). – С. 13-14. 6. Конхоида Никомеда [Электронный ресурс]. – Режим доступа: http://ru.wikipedia.org/wiki/Конхоида_Никомеда.
7. Невсис. Применение [Электронный ресурс]. – Режим доступа: http://ru.wikipedia.org/wiki/Невсис.
6. Приложение
Рисунок 1. Улитка Паскаля.
Три улитки паскаля, конхоиды чёрной окружности: зелёная a>l, красная (кардиоида) a=l и синяя a
В случае l=2a, улитка Паскаля также называется
трисектриса. Такое название она получила из-за того, что если на плоскости задана трисектриса, то трисекцию угла можно построить с помощью циркуля и линейки.
Рисунок 2. Квадратриса.
Рисунок 3. Конхоида Никомеда.
Три конхоиды прямой с общим центром.
Красная l = 2/а
Зелёная l = а
Синяя l = 2а
Рисунок 4. Архимедова спираль.
Рисунок 5. Невсис.
Рисунок 6. Папирофлексия.
Рисунок 7. Чертёж к решению.
Рисунок 8. К Теореме Морлея.
Рисунок 9. К теореме Морлея 2.