1 способ. Обозначим белые - Б1, Б2, Б3, алые - А1,А2, чайные - Ч1, Ч2, Ч3,Ч4
Перечислим возможные варианты
Б1-А1-Ч1, Б1-А1-Ч2, Б1-А1-Ч3, Б1-А1-Ч4, Б1-А2-Ч1,Б1-А2-Ч2, Б1-А2-Ч3, Б1-А2-Ч4
Б2- А1-Ч1, Б2-А1-Ч2, Б2-А1-Ч3, Б2-А1-Ч4, Б2-А2-Ч1,Б2-А2-Ч2, Б2-А2-Ч3, Б2-А2-Ч4
Б3- А1-Ч1, Б3-А1-Ч2, Б3-А1-Ч3, Б3-А1-Ч4, Б3-А2-Ч1,Б3-А2-Ч2, Б3-А2-Ч3, Б3-А2-Ч4

Ответ: 24 варианта.

2способ. Дерево возможностей



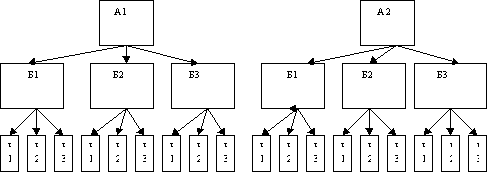
 3 способ. Используя правило умножения, получаем: 2х3х4=24

20. К 60-летию Победы группа школьников отправилась по местам боевых действий в Смоленской области. Они планировали осуществить поход по маршруту деревни Сосновка-Быковка- Масловка- Видово. Из С в Б можно проплыть по реке или пройти пешком, из Б в М- пешком или на автобусе, из М в В - по реке, пешком или автобусе. Сколько вариантов похода есть у щкольников?

1 способ. Обозначим СБ - путь из Сосновки в Бытовку, ВГ - путь из Быковки в Масловку, МВ - путь из Масловки в Видово.
По реке -Р, пешком - П, на автобусе - А
Перечислим возможные варианты:
СБР- БМП-МВР, СБР- БМП-МВП, СБР- БМП-МВА
СБР-БМА-МВР, СБР-БМА-МВП, СБР-БМА-МВА
СБА- БМП-МВР, СБА- БМП-МВП, СБА- БМП-МВА
СБА-БМА-МВР, СБА-БМА-МВП, СБА-БМА-МВА
Ответ: 12 вариантов.

2 способ. Дерево возможностей



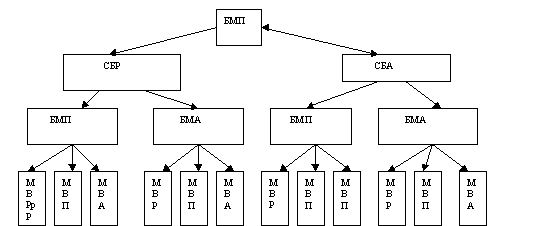
Список использованной литературы:

1. 
   Бахтина, Т. П. Готовимся к олимпиадам, турнирам и математическим боям / Т. П. Бахтина. — Мн.: АВЕРСЭВ, 2002. — 253 с.
   
2. 
   Горбачев, Н.В. Сборник олимпиадных задач по математике / Н. В. Горбачев. — Москва: Просвещение, 2004. — 600 с.
   
3. 
   Клименченко, Д. В. Задачи по математике для любознательных / Д. В. Клименченко. — Москва: Просвещение, 1992. — 192 с.
   
4. 
   Шарыгин, И. Ф. Задачи на смекалку / И. Ф. Шарыгин, А. В. Шевкин. — М.: Просвещение, 2003. — 93 с.
   
5. 
   Петраков А.С.«Математика для любознательных», Москва:Просвещение, 2002г.
   
6. 
   Атанасян Л.С. Геометрия 7-9. М.: Просвещение, 2005. - 335 с.
   
7. 
   Гусев В.А., Медяник А.И. Дидактические материалы по геометрии для 7 класса. М.: Просвещение, 1991. – 80с.
   
8. 
   Далингер В.А. Планиметрические задачи на построение. Омск: Изд-во ОГПИ, 1999. - 78 с.
   
9. 
   Ильина Н.И. Геометрические построения на плоскости. М.: Школа - пресс, 1997. - 172 с.
   
10. 
    Манин И.Ю. О разрешимости задач на построение с помощью циркуля и линейки // Энциклопедия элементарной математики. М.: Физматгиз, 1963. Т. 4: Геометрия. С. 205-227.
    
11. 
    Олимпиадные задания по математике. 5–8класс/авт.-сост. С.П. Ковалева.–Волгоград: Учитель, 2007.–88с.
    
12. 
    Погорелов А.В. Геометрия, 7–11. М.: Просвещение, 1992
    
13. 
    Прасолов В.В. Три классические задачи на построение. М.: Наука, 1992. 80 с.
    
14. 
    Энциклопедия для детей. Т. 11. Математика/Ред. коллегия: М.Аксенова, В.Володин и др. – М.: Аванта+, 2005.
    
15. 
    Коренева В.Е. Решение задач на построение методом спрямления. Математика в школе.1995г. №5
    
16. 
    Клименченко С.В., Цикунова Т.Д. Задачи на построение треугольников по некоторым данным точкам. Математика в школе. 1990г. №1
    
17. 
    Белошистая А.В. Задачи на построение в школьном курсе геометрии. Математика в школе. 2002г. №9
    

---

---

Смотрите также файлы

• 8 семестр Приложение 1 Образовательная автономная некоммерческая организация.docx

• Виды отпусков сотрудников органов внутренних дел и порядок их оформления.docx

• 8сынып География пнінен 3тосана арналан жиынты баалауды тапсырмалары.docx

• Гиперсілтемелер Сабаты масаты.pptx

• Производственная практика по специальности 44. 02. 01 Дошкольное образование.docx