Файл: Урок 37. Формулы приведения. Перечень вопросов, рассматриваемых в теме формулы приведения.docx
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 11.01.2024
Просмотров: 50
Скачиваний: 1
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
В остальных формулах, где в левой части присутствуют
или 
, синус меняется на косинус и наоборот, а тангенс на котангенс.Формул приведений много и их не обязательно каждый раз выводить и запоминать.
Для этого придумали мнемоническое правило.
-
Если в левой части присутствуют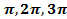
и т.д. синусы, косинусы и тангенсы не меняются.
Если в левой части присутствуют
или , синус меняется на косинус, косинус на синус, тангенс на котангенс.-
Знак в правой части ставим тот же, который имело исходное число в левой части, при условии
.
Существует легенда про рассеянного математика, который всё время забывал менять или не менять синус на косинус и наоборот. Он смотрел на свою сообразительную лошадь и она кивала головой вдоль той оси, где стояли числа
и , 
. (рис. 3)
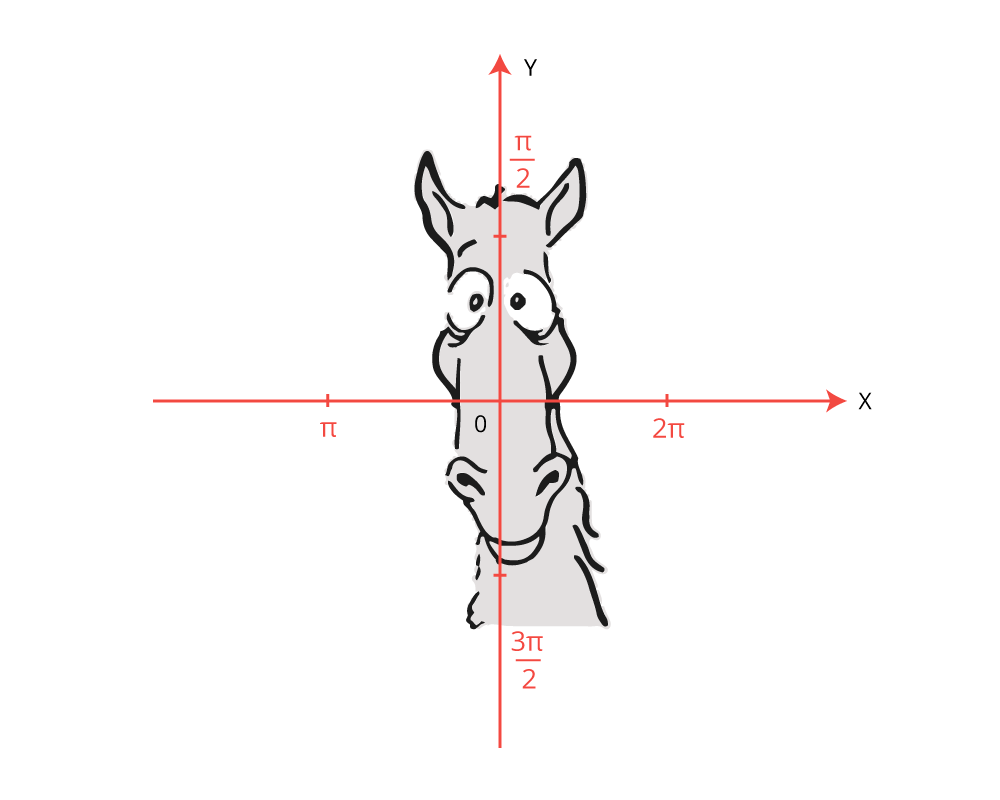
Рисунок 3 – «правило лошади»
Если аргумент содержал
или 
, лошадь кивала вдоль оси Оу. Это означало «да, менять». А если 
, кивала вдоль оси Ох – «не менять».Так же помните: чётные числа вида
и т.д. находятся на оси Ох справа от нуля на единичной окружности, а нечётные 
и т. д. слева от нуля.Если в выражении перед
стоит плюс, то точка перемещается по окружности по часовой стрелке, если стоит минус, то против часовой стрелке.Примеры и разбор решения заданий тренировочного модуля
Пример 1: упростите выражение
.
находится на оси Ох, слева от нуля, косинус не меняем. Перед минус, точка перемещается против часовой стрелке и попадает во вторую четверть, здесь косинусы отрицательные (рис.4)
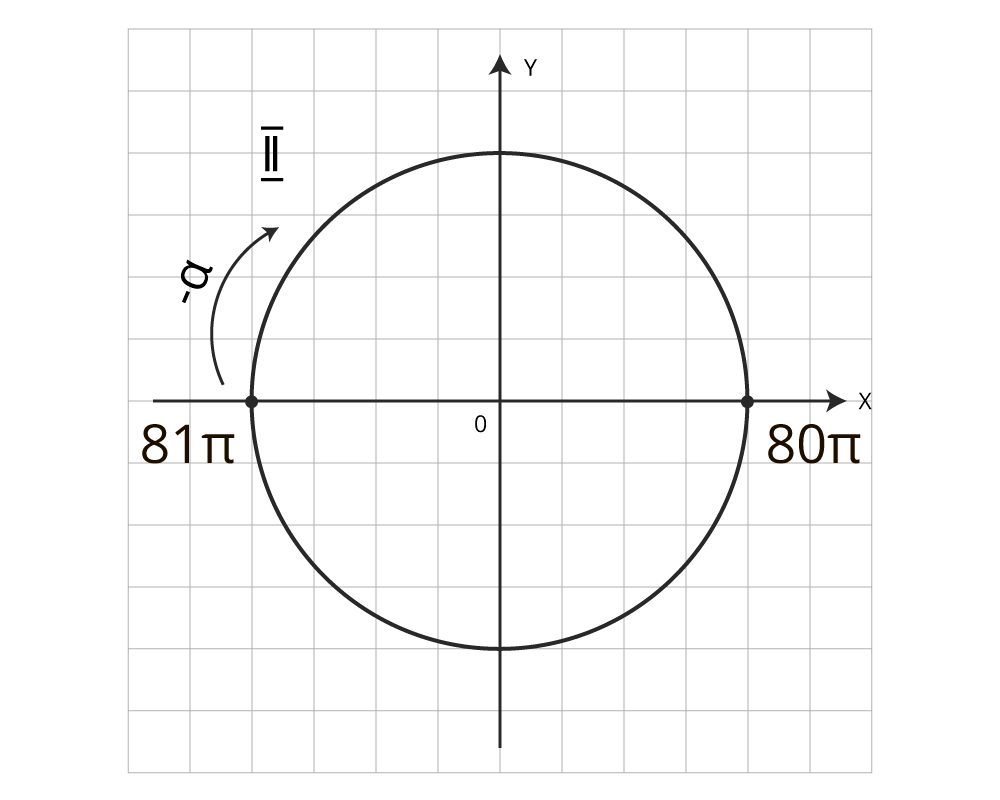
Рисунок 4 – перемещение точки по единичной окружности
Значит
=
.Пример 2: вычислите
Преобразуем выражение в скобке:
. 
находится слева на оси Ох, синус не меняем. Угол в третьей четверти, синусы отрицательные.