Файл: Курсовой проект тема Студент Колтыга И. А. Руководитель Смирнов Н. Н.doc
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 11.01.2024
Просмотров: 96
Скачиваний: 1
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
(30)
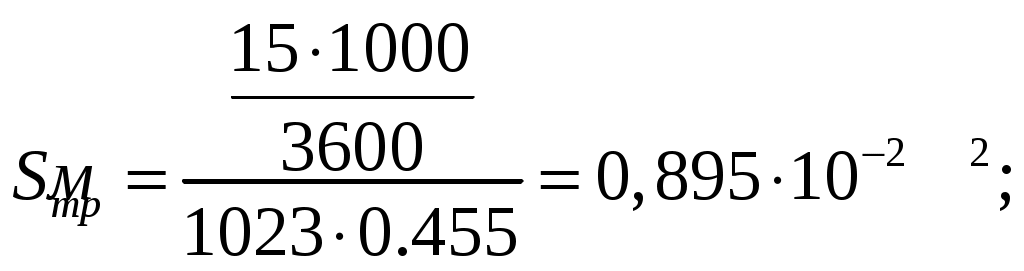
4.3.2 Ориентировочный выбор подогревателя.
Для обеспечения турбулентного режима номинальная площадь проходного сечения должна быть меньше рассчитанной. Коэффициент теплоотдачи от конденсирующегося пара не зависит от режима течения в межтрубном пространстве, следовательно, необязательно рассчитывать скорость движения пара и проходное сечение межтрубного пространства
Выбор теплообменных аппаратов производится по проходному сечению трубного пространства / 3, табл. 2.3 /.
4.3.3. Параметры подогревателя необходимые для уточнённого расчёта.
Подача горячего теплоносителя - в межтрубное пространство
Направление потоков – противоток
Расположение аппарата - горизонтальное
Расположение труб – шахматное
Наличие перегородок – есть
Аппарат шестиходовой
.
5. Подробный расчет теплообменного аппарата
5.1 Теплоотдача в трубах
По (/1/, табл. 4.1, стр. 151) находим, что теплоотдача для раствора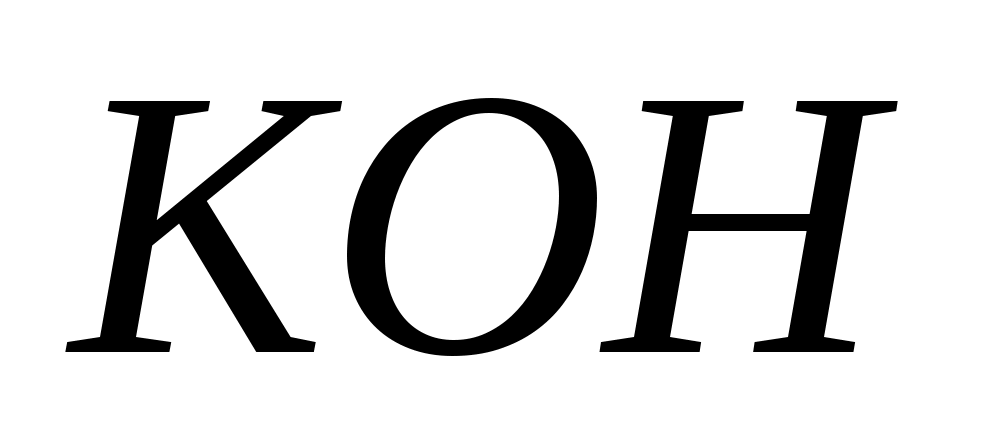 описывается уравнением:
описывается уравнением:

где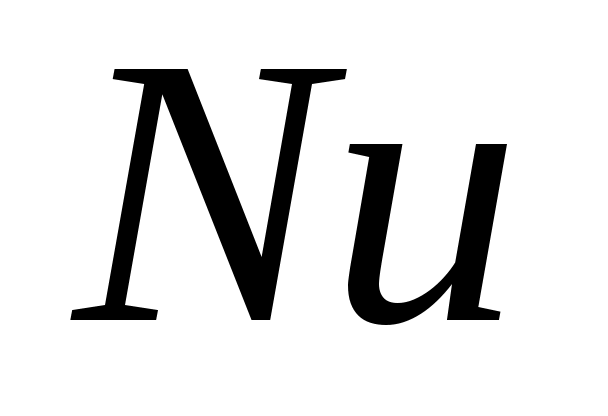 - критерий Нуссельта;
- критерий Нуссельта;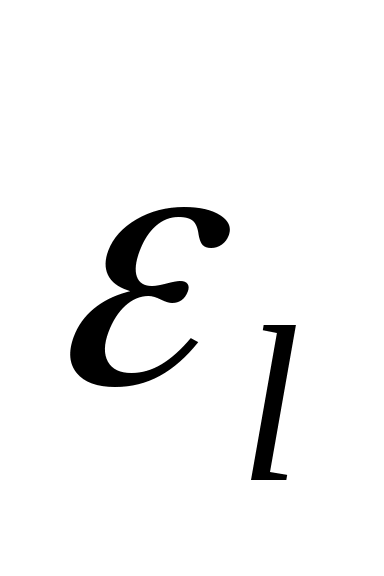 - поправочный коэффициент; Re – критерий Рейнольдса; Pr – критерий Прандтля;
- поправочный коэффициент; Re – критерий Рейнольдса; Pr – критерий Прандтля; 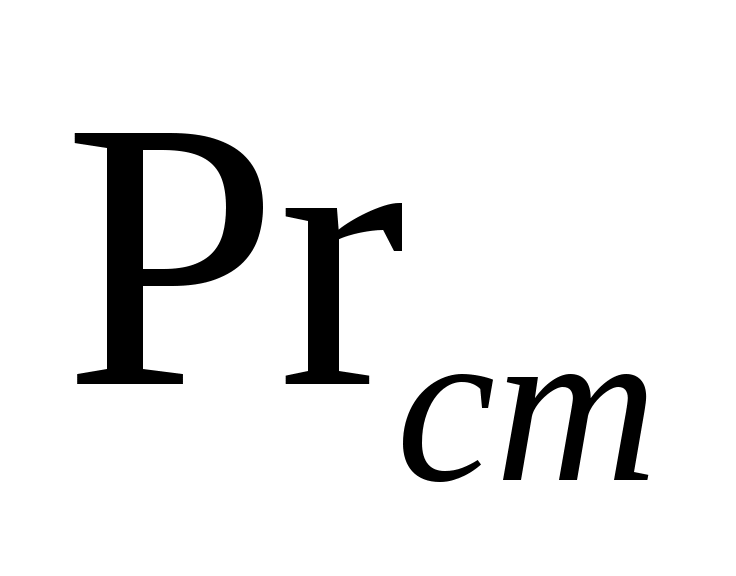 - критерий Прандтля при температуре стенки трубы.
- критерий Прандтля при температуре стенки трубы.
Коэффициент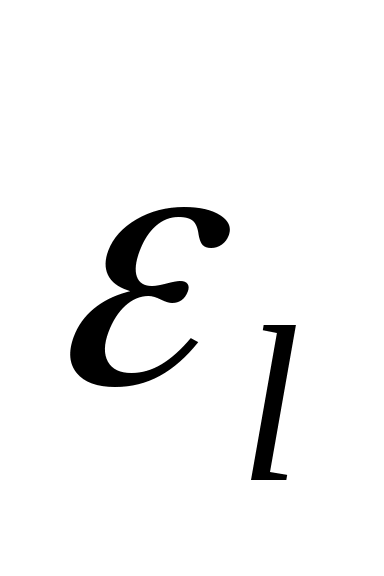 примем равным 1, полагая, что
примем равным 1, полагая, что 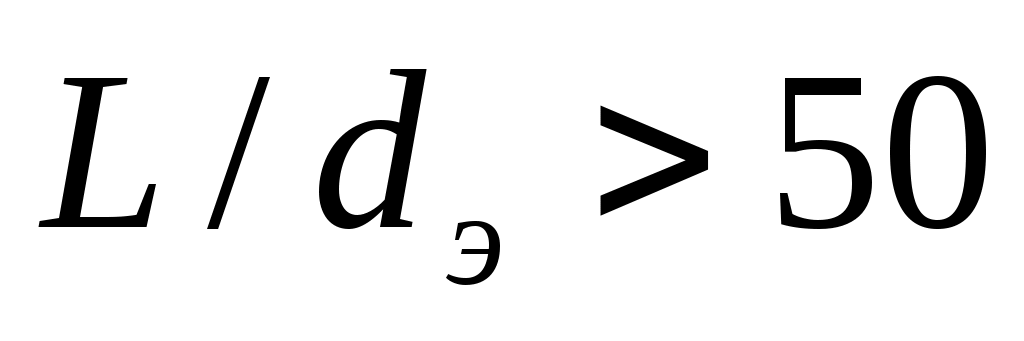 (/1/, табл. 4.3, стр. 153), где
(/1/, табл. 4.3, стр. 153), где 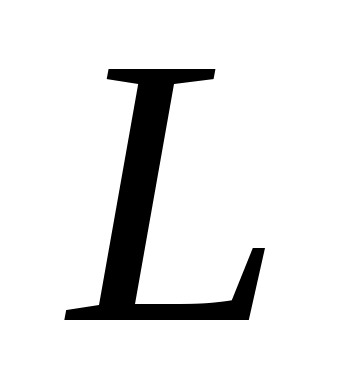 - длина труб,
- длина труб, 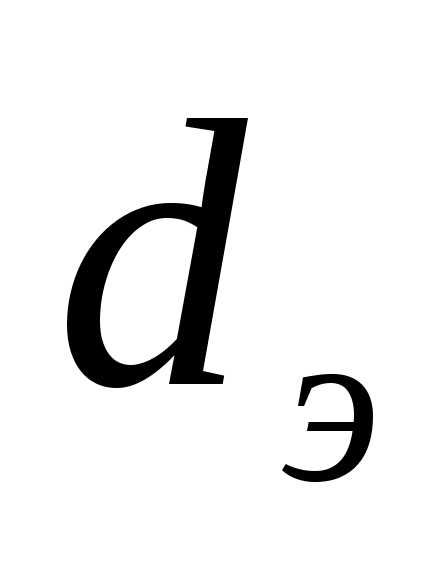 - эквивалентный диаметр. Критерий Рейнольдса рассчитываем по формуле:
- эквивалентный диаметр. Критерий Рейнольдса рассчитываем по формуле:
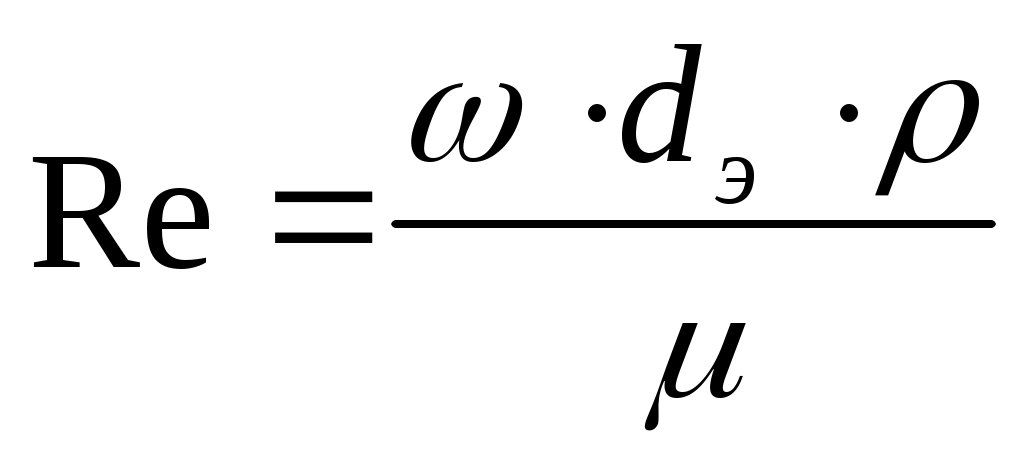
где - средняя скорость потока,
- средняя скорость потока, 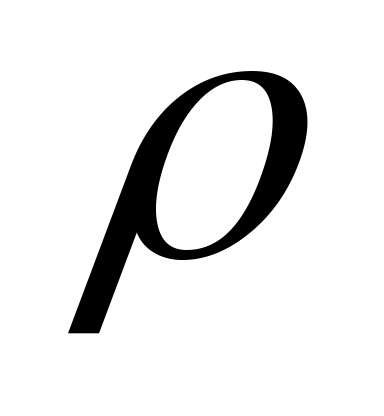 и
и 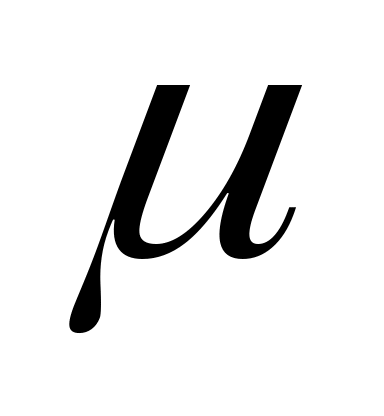 - соответственно плотность раствора и динамический коэффициент вязкости, при средней температуре
- соответственно плотность раствора и динамический коэффициент вязкости, при средней температуре 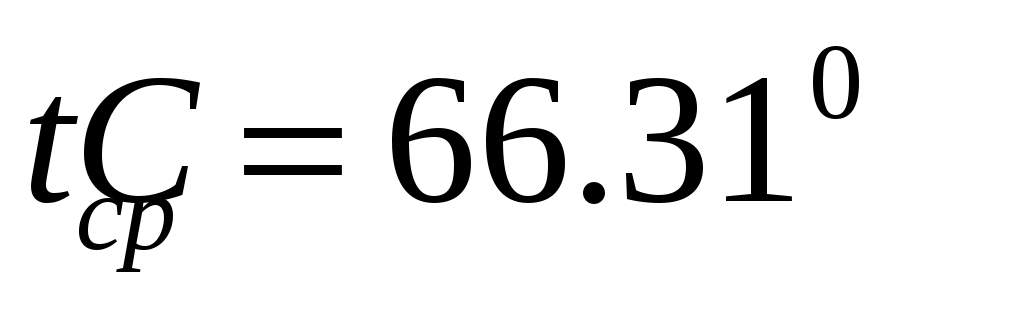 .
.
По формуле 3.7 плотность раствора при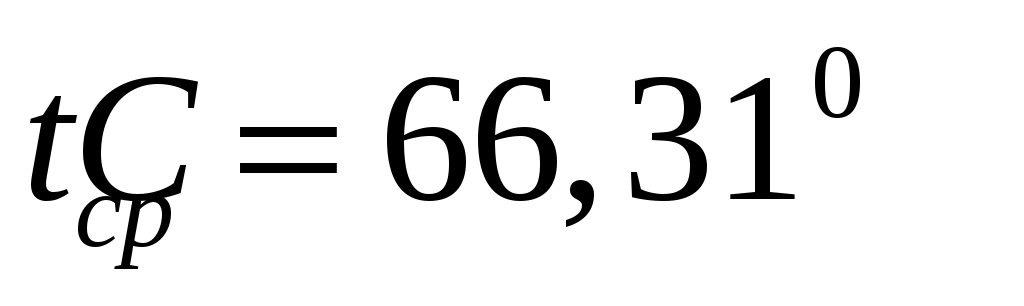 и
и 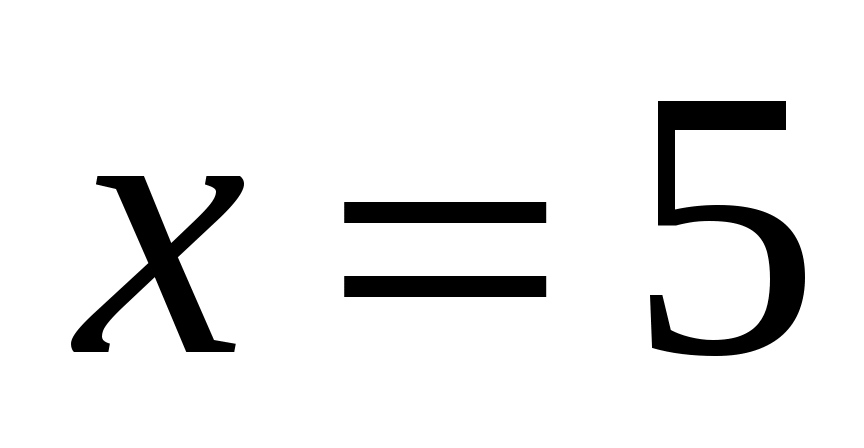 % масс. равняется:
% масс. равняется:

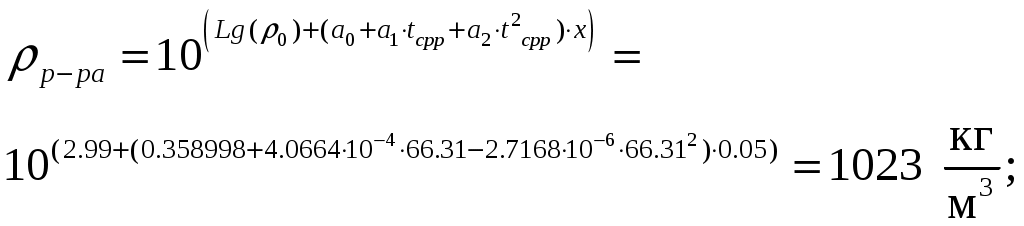
Среднюю скорость потока определяем по формуле:
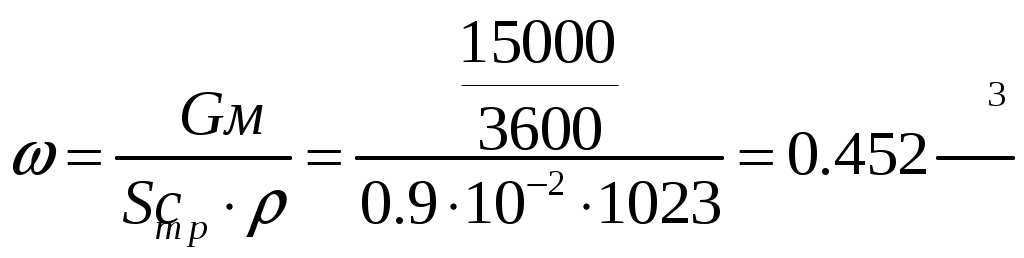
Учитывая, что для труб круглого сечения диаметр труб и эквивалентный диаметр совпадают, то для труб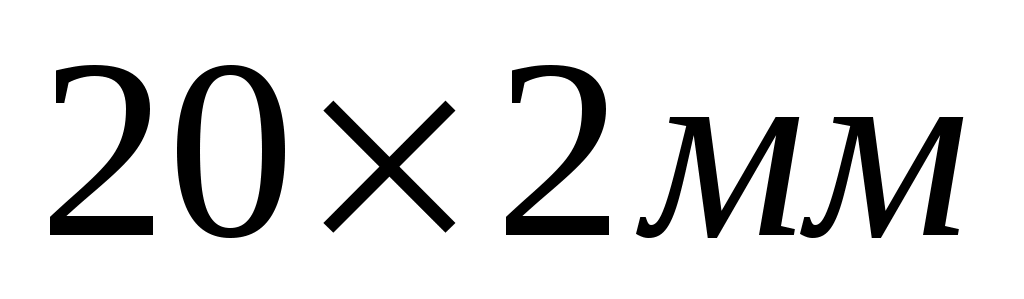 получаем:
получаем:
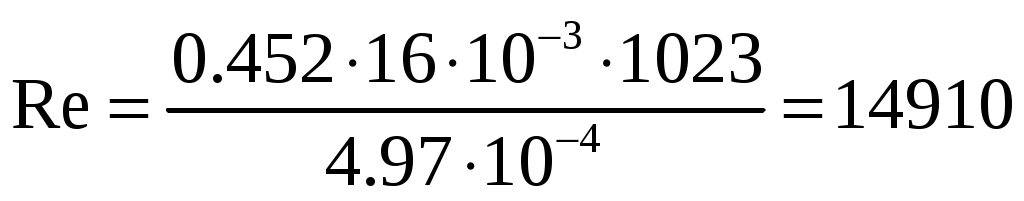 .
.
Критерий Прандтля находим по формуле:
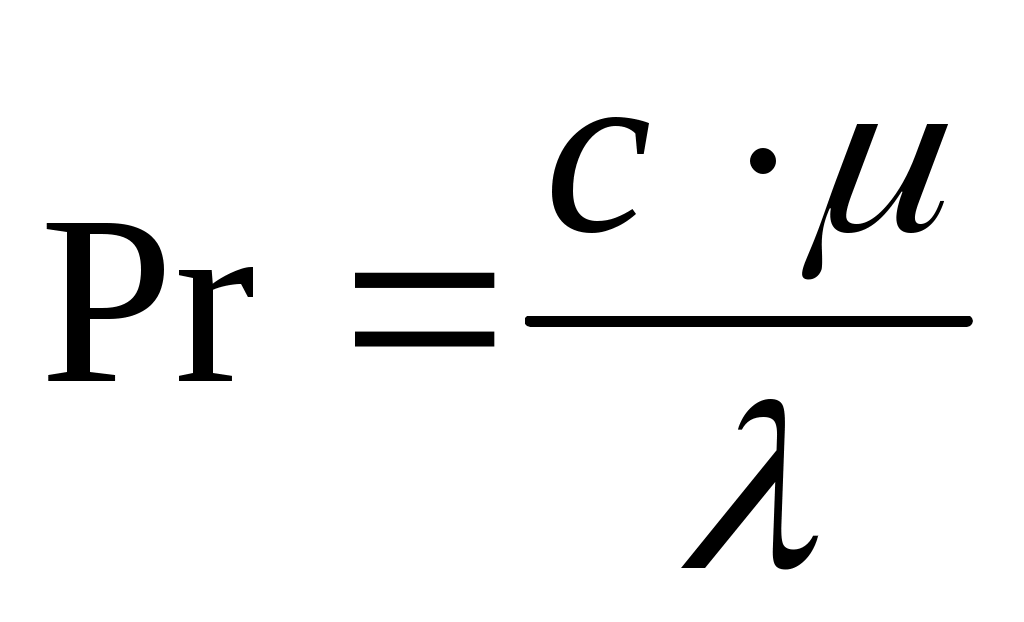 (3.27)
(3.27)
где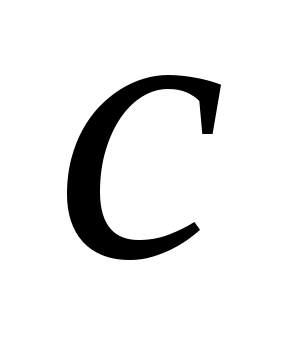 - удельная теплоемкость,
- удельная теплоемкость, 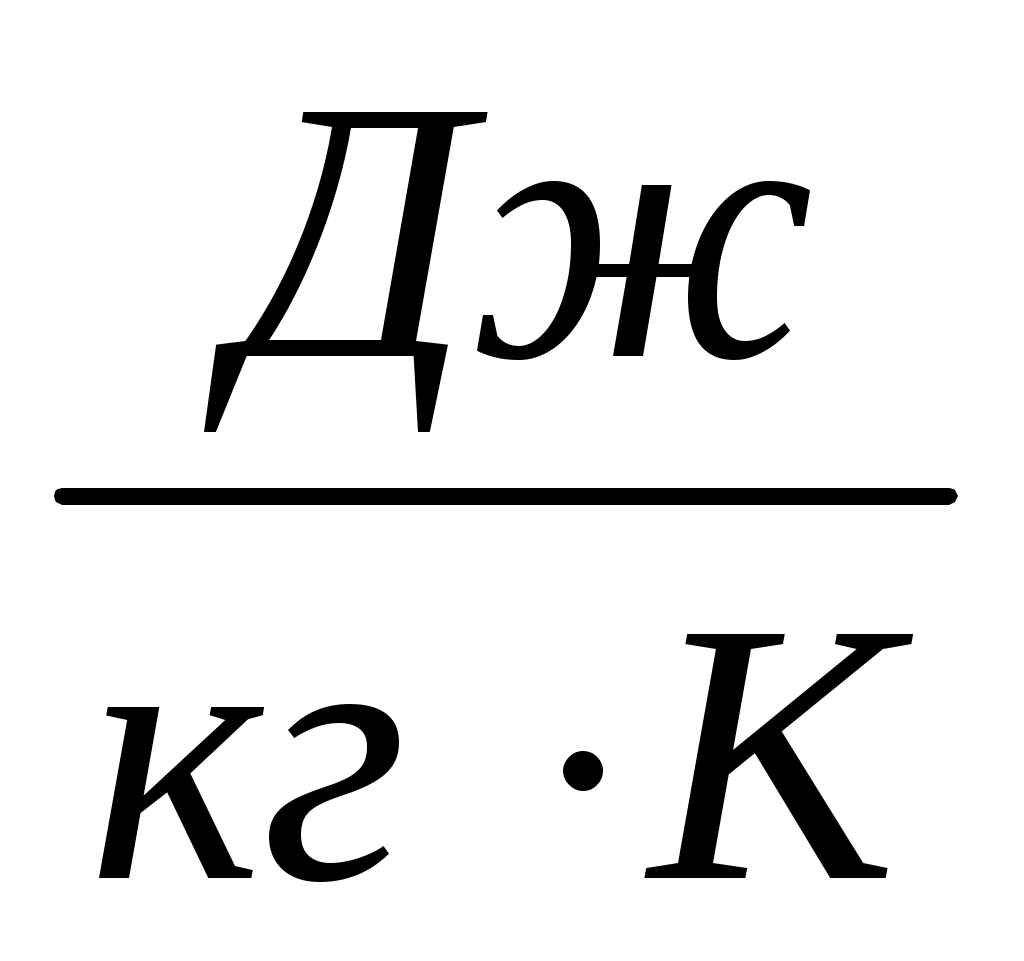 ;
; 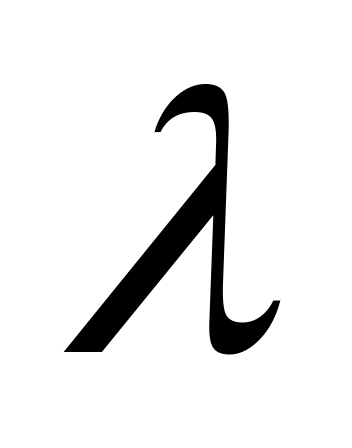 - коэффициент теплопроводности,
- коэффициент теплопроводности, 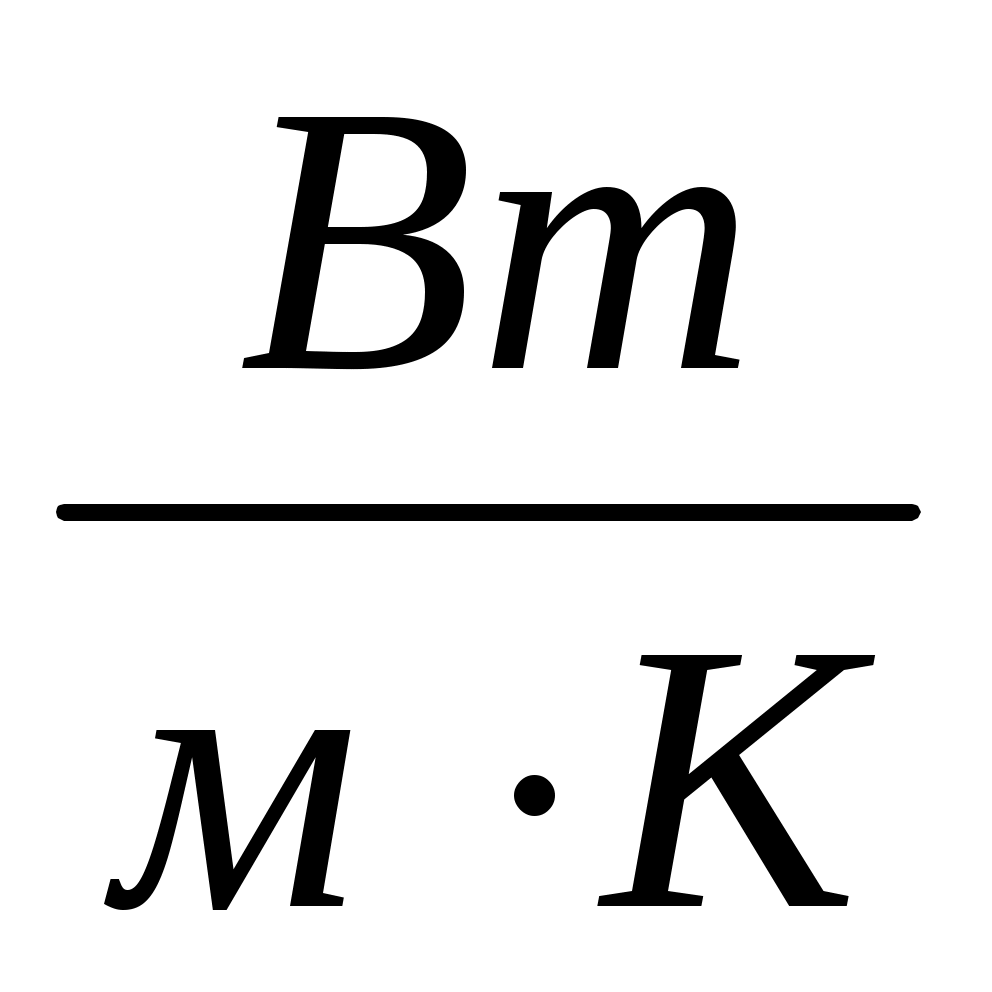 ;
;
 - динамический коэффициент вязкости,
- динамический коэффициент вязкости, 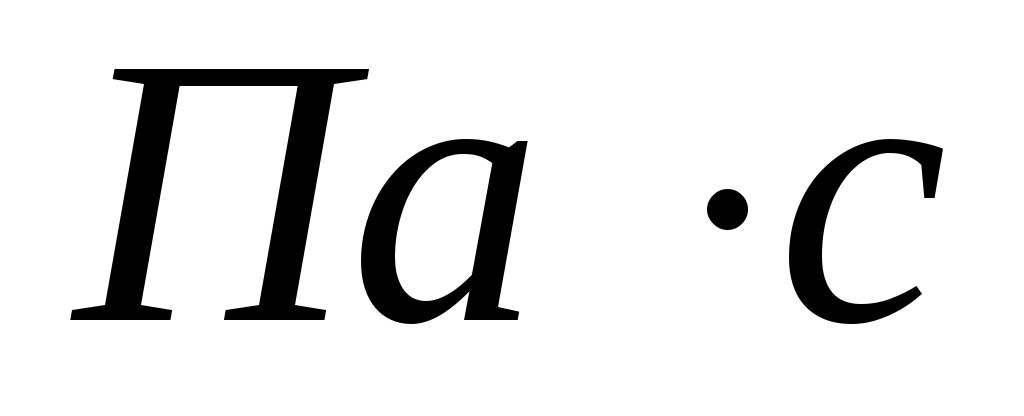 .
.
Коэффициент теплопроводности при и
и  % масс. по формуле 3.15 равняется:
% масс. по формуле 3.15 равняется:
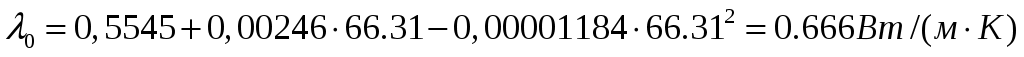 ,
,
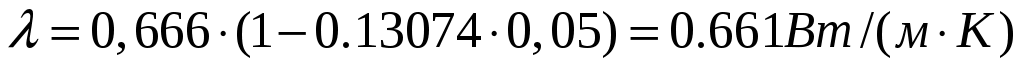 .
.
Таким образом, критерий Pr при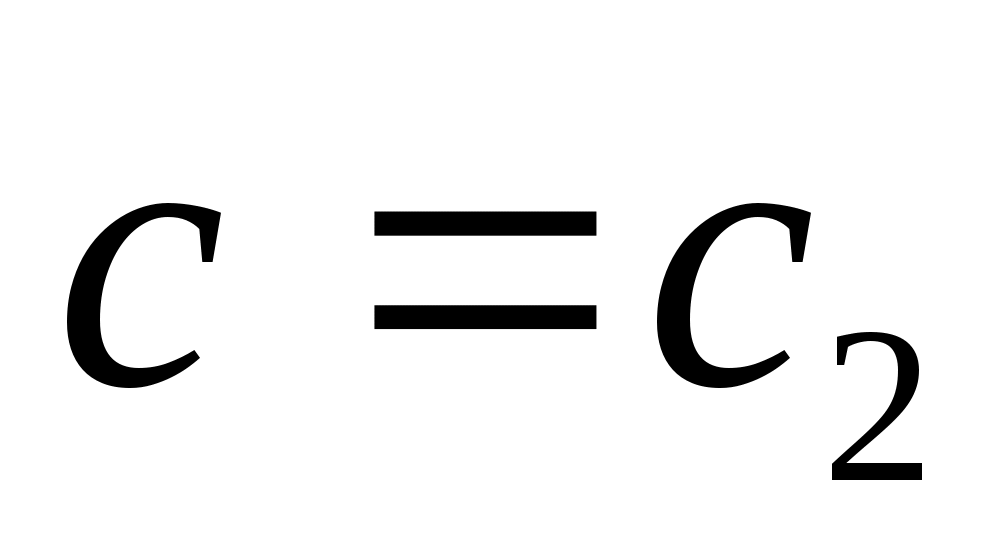 и
и 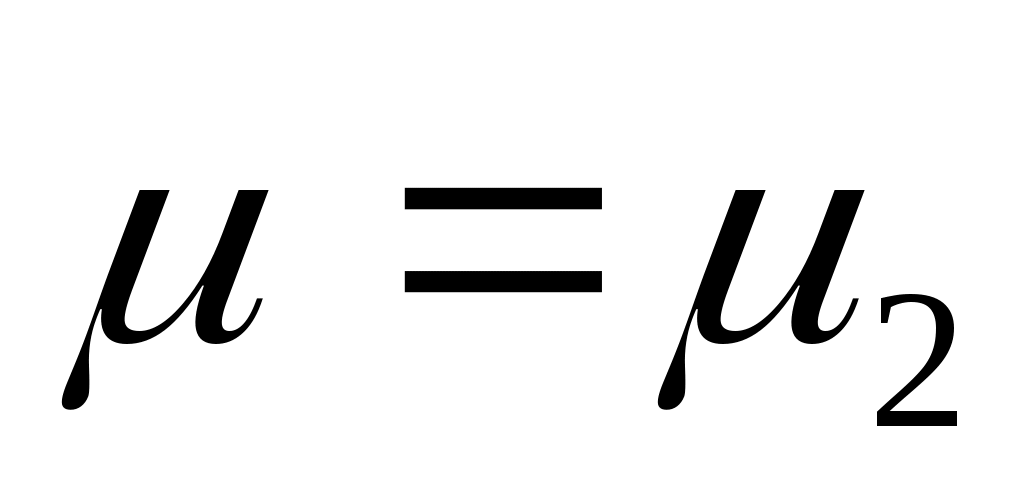 равняется:
равняется:
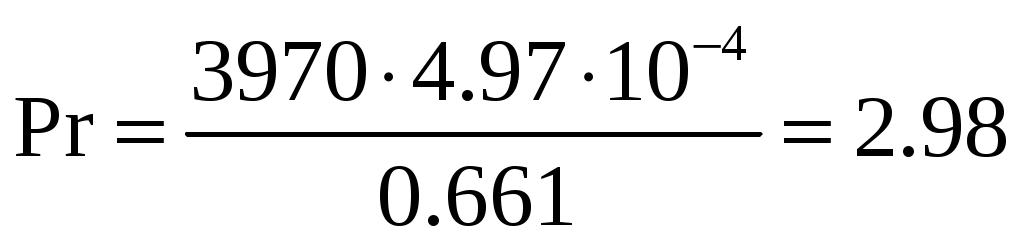
Коэффициент теплоотдачи от раствора к стенке:
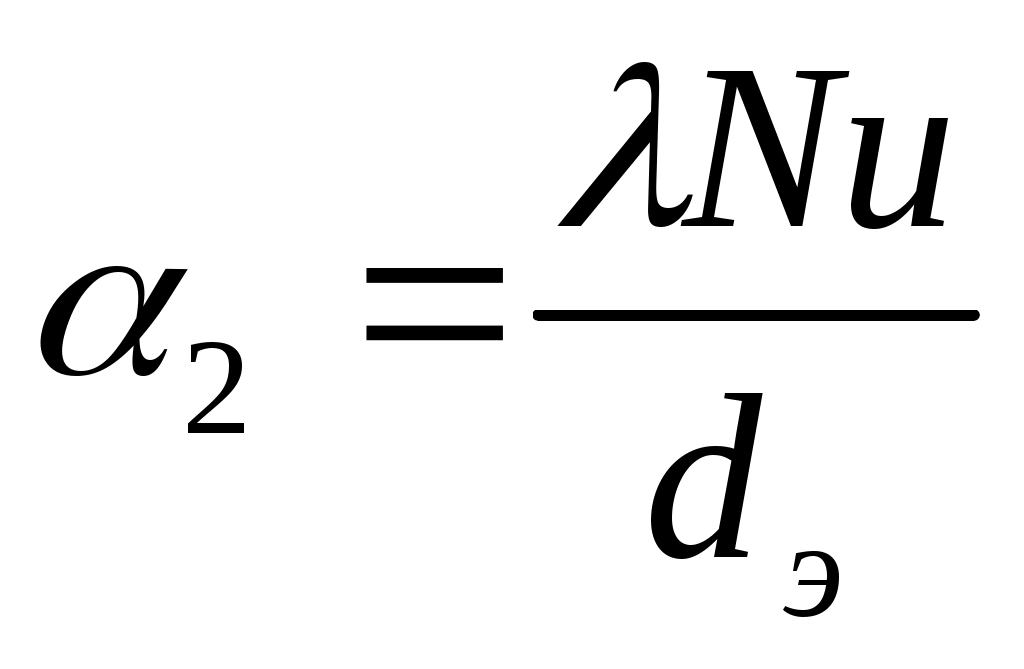 .
.
С учетом формулы 3.25 получаем:
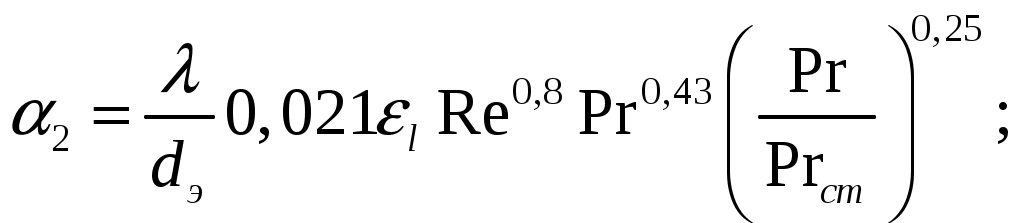
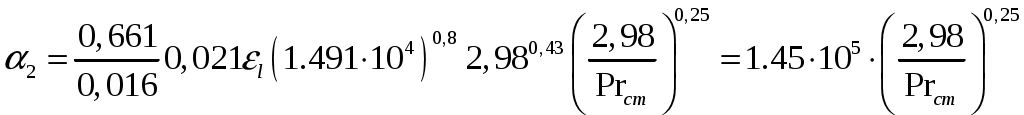
5.2 Теплоотдача при пленочной конденсации водяного пара
Для водяного пара в случае конденсации на пучке горизонтальных труб осредненный по всему пучку коэффициент теплопередачи
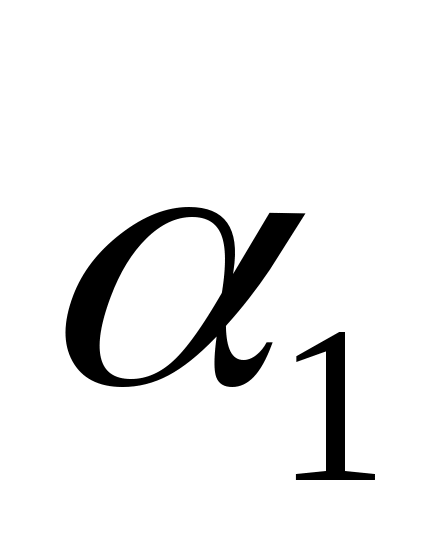 можно рассчитать по формуле:
можно рассчитать по формуле:
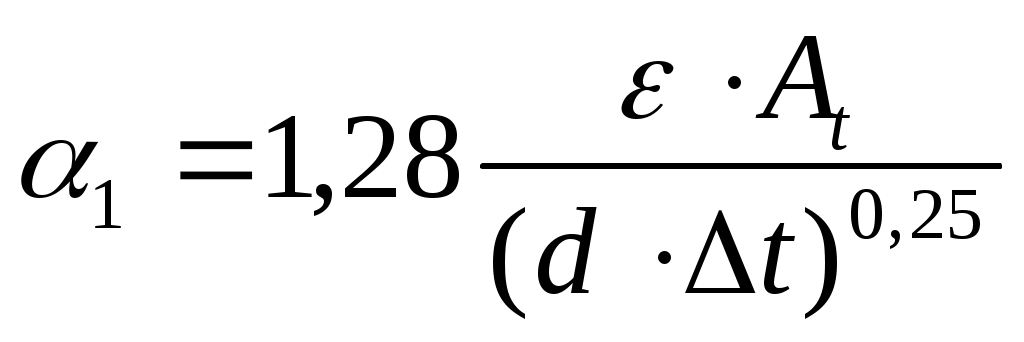 ,
,
где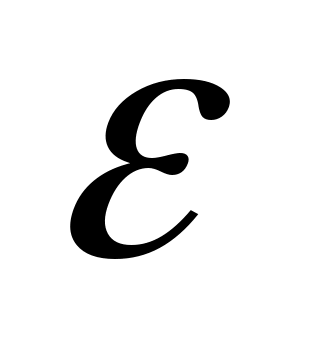 - поправочный множитель, учитывающий влияние числа труб по вертикали;
- поправочный множитель, учитывающий влияние числа труб по вертикали; 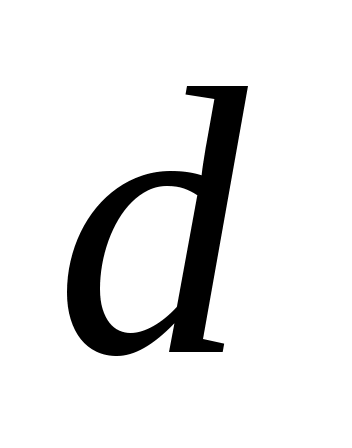 - наружный диаметр труб;
- наружный диаметр труб; 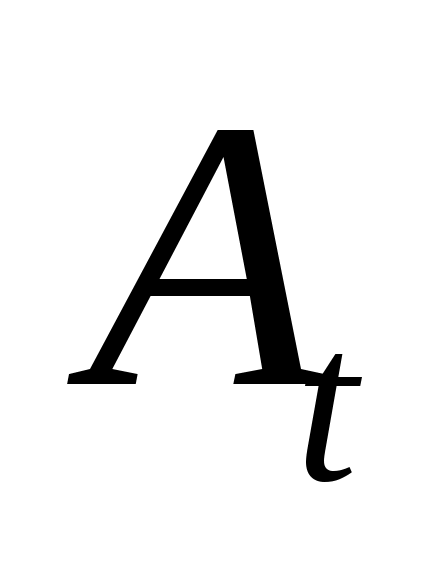 =7240 (взято из /1/, табл.4.6, стр. 162 при температуре конденсации греющего пара);
=7240 (взято из /1/, табл.4.6, стр. 162 при температуре конденсации греющего пара);  - разность средней температуры конденсации греющего пара
- разность средней температуры конденсации греющего пара  и температуры стенки со стороны греющего пара
и температуры стенки со стороны греющего пара  :
:
 .
.
Поправочный множитель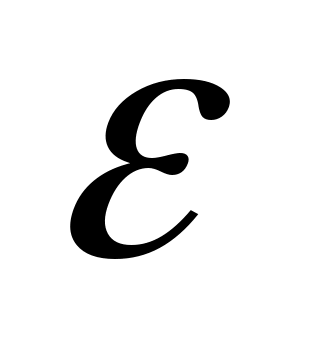 находим по (/1/, рис. 4.7, стр. 162) для шахматного расположения труб и при числе рядов труб по вертикали
находим по (/1/, рис. 4.7, стр. 162) для шахматного расположения труб и при числе рядов труб по вертикали 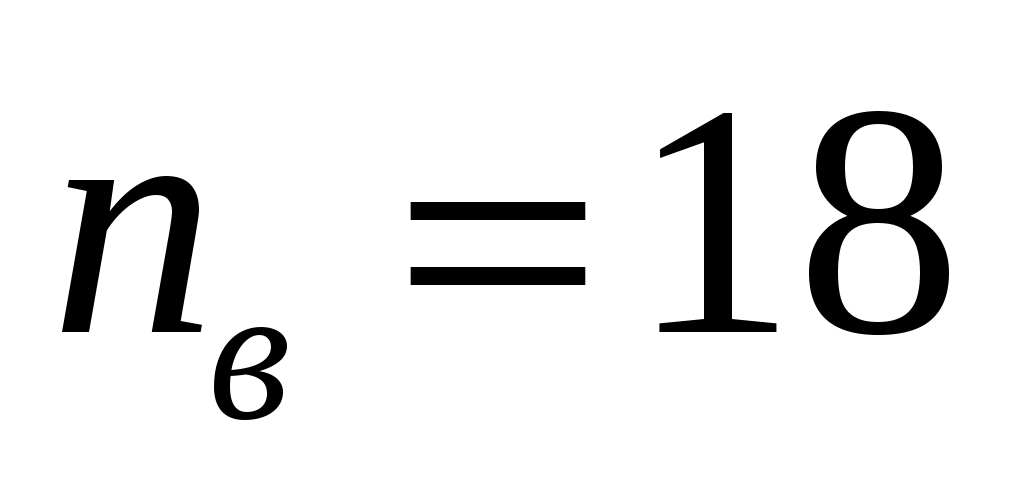 :
:
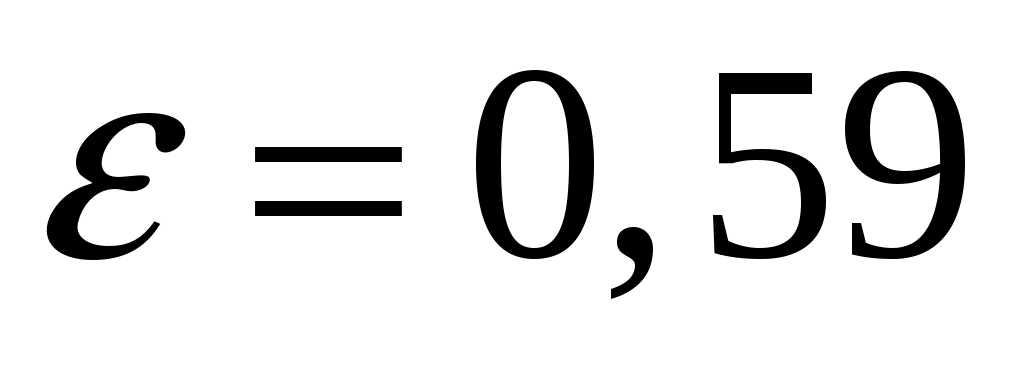 .
.
Имеем:
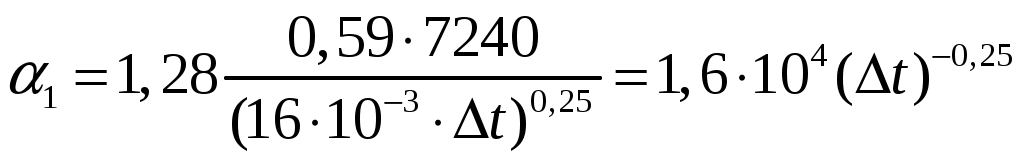
5.2.1 Расчет коэффициента теплопередачи
Первое приближение.
Принимаем в первом приближении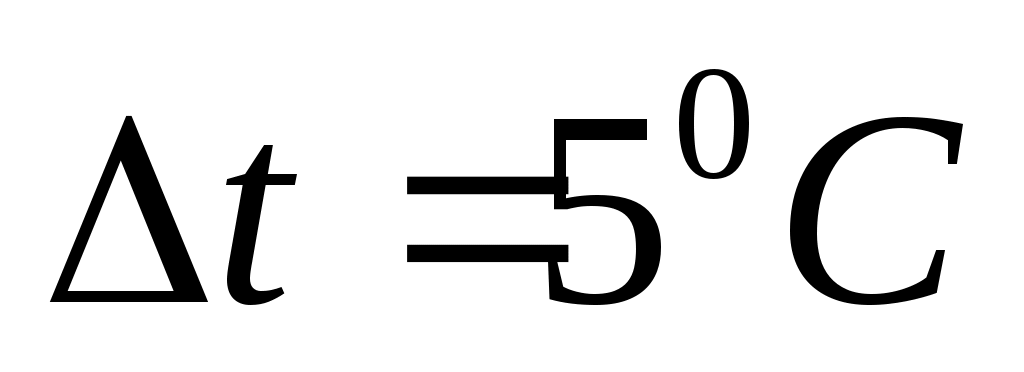 . Тогда температура стенки со стороны греющего пара равняется:
. Тогда температура стенки со стороны греющего пара равняется:
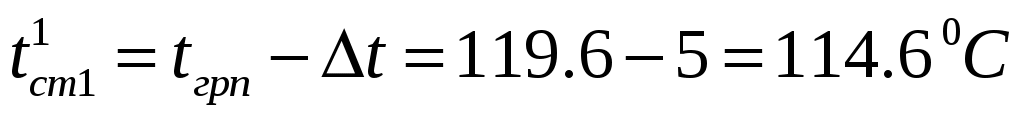 .
.
Тогда по формуле (3.29) получаем:
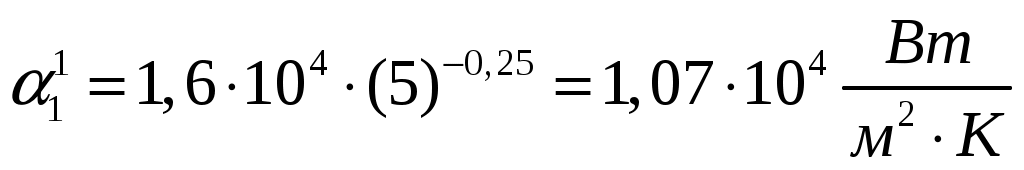 .
.
При этом удельный тепловой поток от пара к стенке равен:
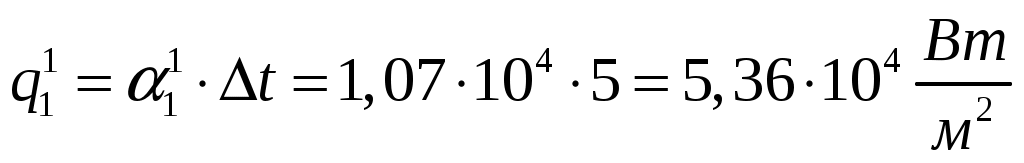 .
.
Сумма термических сопротивлений равна:
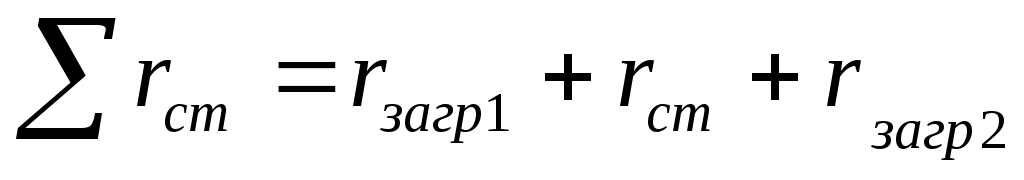 ,
,
где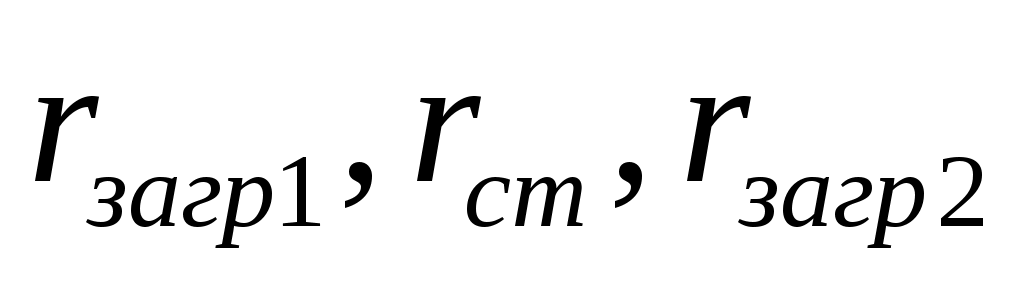 - соответственно термические сопротивления загрязнений со стороны греющего пара, стенки и со стороны раствора.
- соответственно термические сопротивления загрязнений со стороны греющего пара, стенки и со стороны раствора.
По (/1/, табл. XXXI, стр. 531) находим:
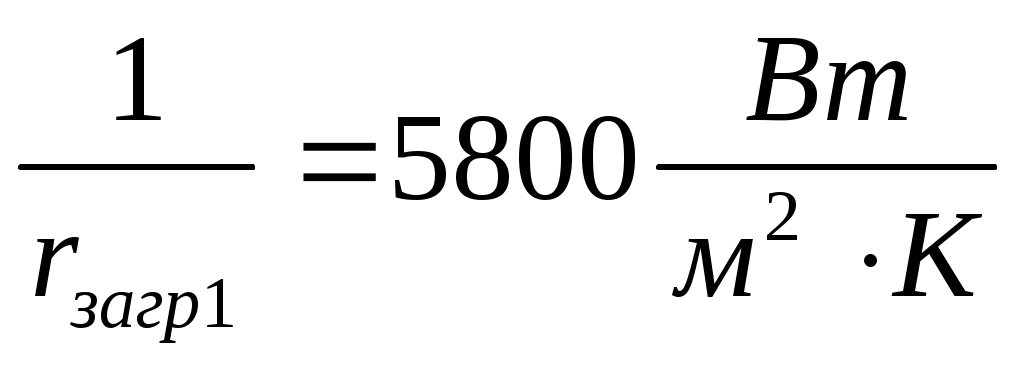 ,
,
Для стенки:
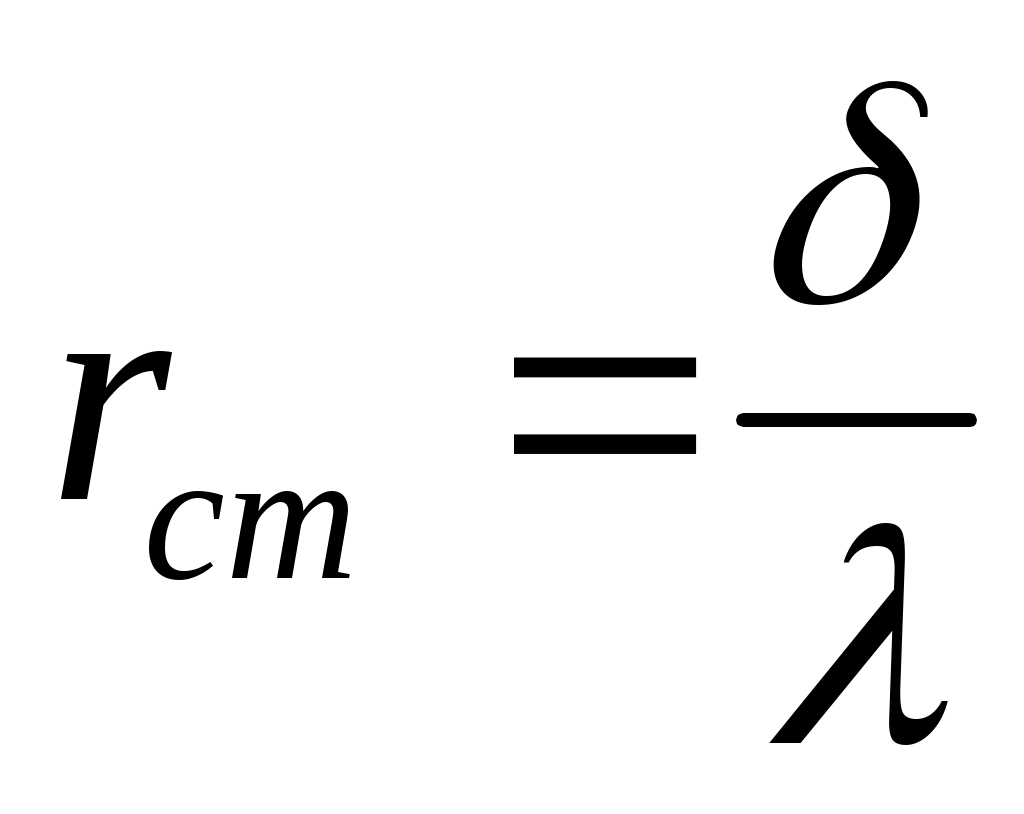 ,
,
где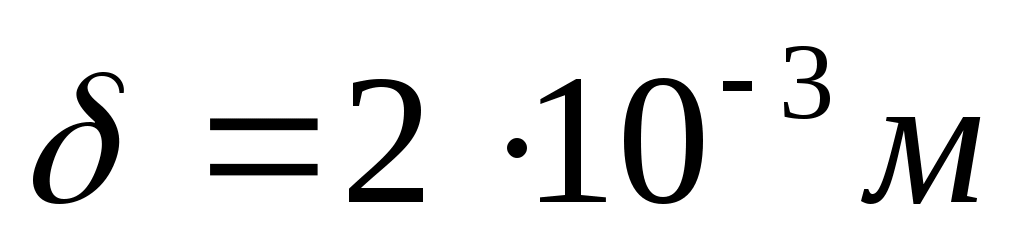 - толщина стенки,
- толщина стенки, 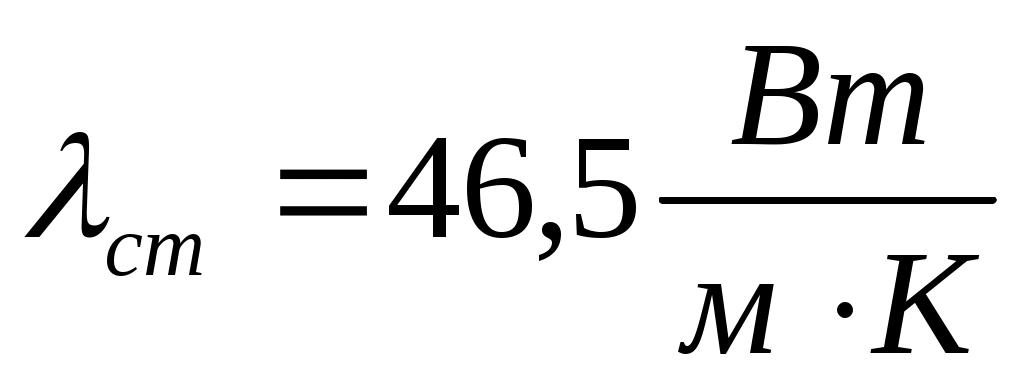 - коэффициент теплопроводности стали (/1/, табл. XXVIII, стр. 529).
- коэффициент теплопроводности стали (/1/, табл. XXVIII, стр. 529).
 ,
,
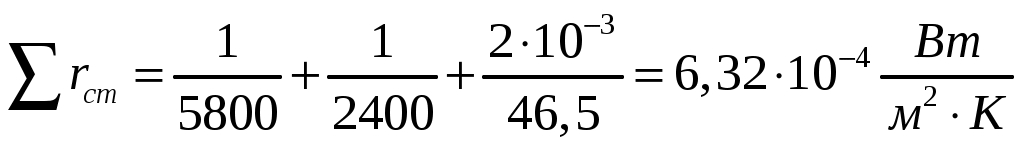 .
.
Поскольку удельный тепловой поток от пара к стенке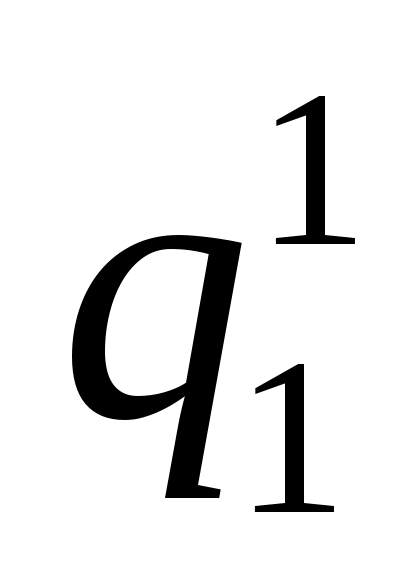 равен удельному тепловому потоку через стенку
равен удельному тепловому потоку через стенку 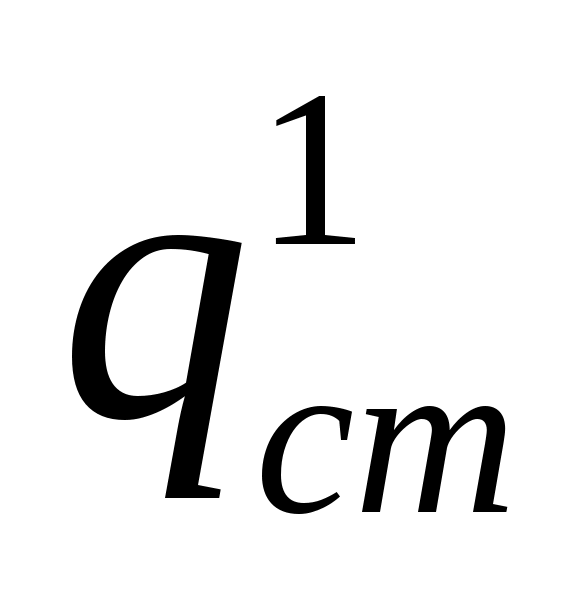 , то можно получить:
, то можно получить:
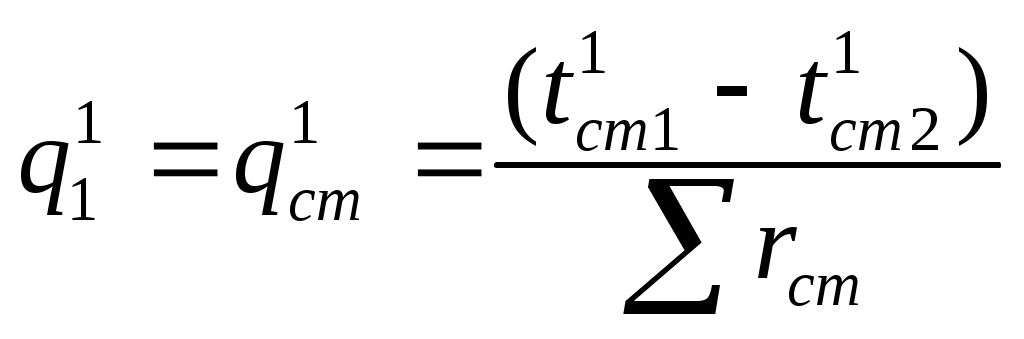 ,
,
при этом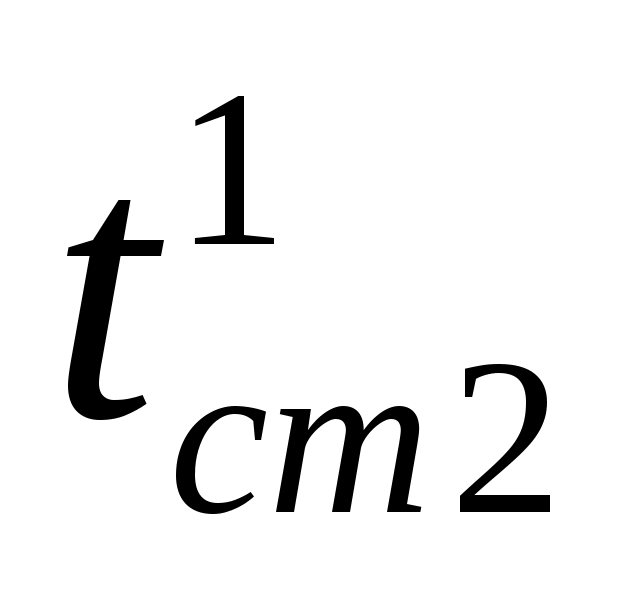 - температура стенки со стороны раствора равна:
- температура стенки со стороны раствора равна:
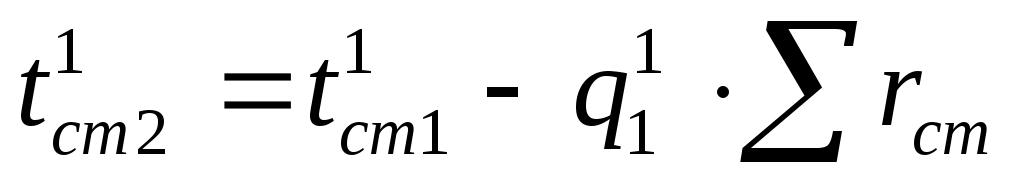 ,
,
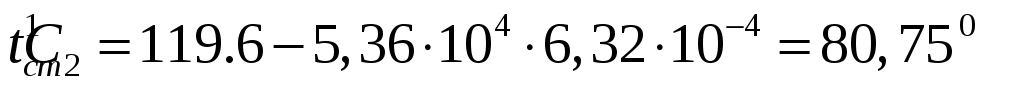 .
.
При температуре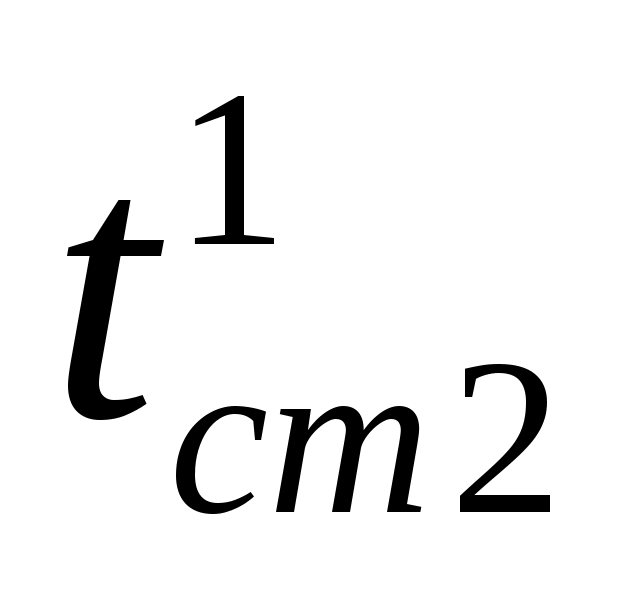 удельная теплоемкость, динамический коэффициент вязкости и коэффициент теплопроводности, вычисленные, соответственно, по формулам 3.11, 3.15, 3.20 равны:
удельная теплоемкость, динамический коэффициент вязкости и коэффициент теплопроводности, вычисленные, соответственно, по формулам 3.11, 3.15, 3.20 равны:
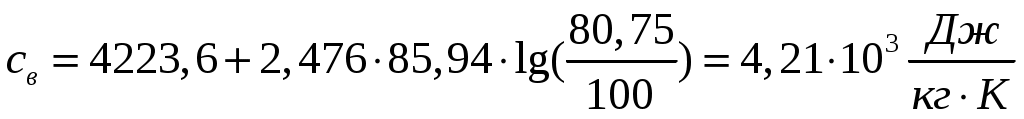 ,
,
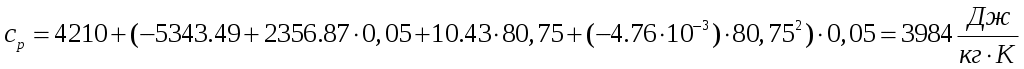
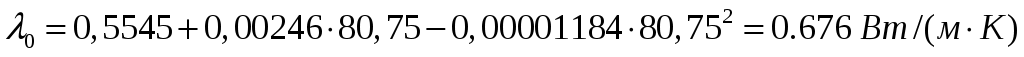 ,
,
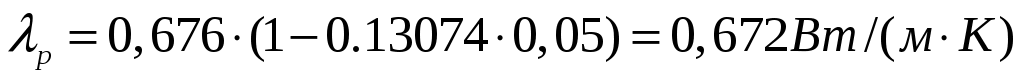 ;
;
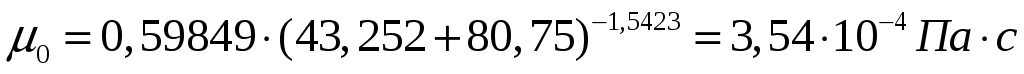 ,
,
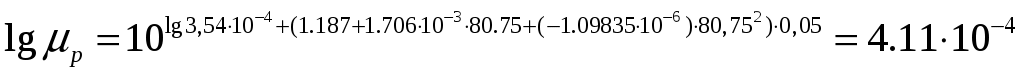
Подставляя найденные значения в формулу 3.27, получаем значение критерия Прандтля при температуре стенки:

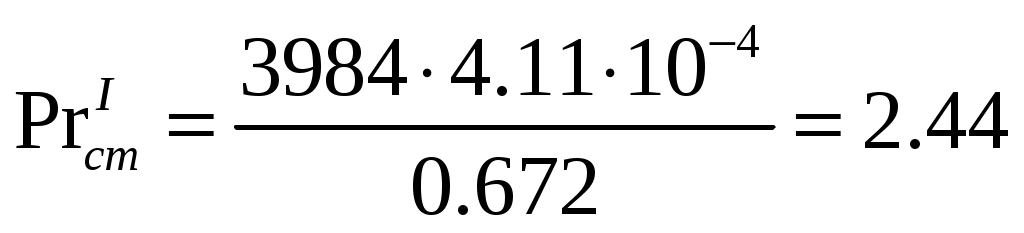
По формуле 3.28 находим в коэффициент теплоотдачи от раствора к стенке:
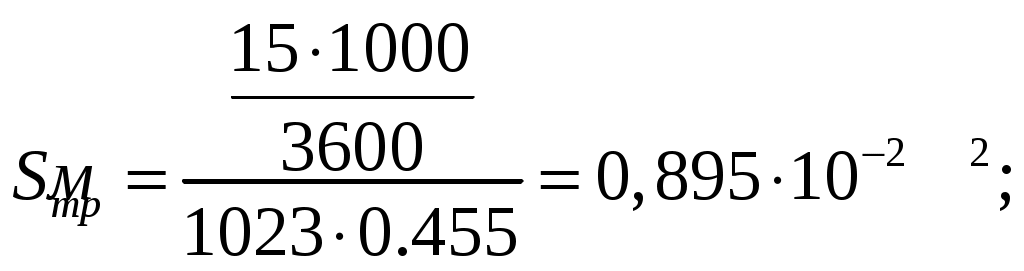
4.3.2 Ориентировочный выбор подогревателя.
Для обеспечения турбулентного режима номинальная площадь проходного сечения должна быть меньше рассчитанной. Коэффициент теплоотдачи от конденсирующегося пара не зависит от режима течения в межтрубном пространстве, следовательно, необязательно рассчитывать скорость движения пара и проходное сечение межтрубного пространства
Выбор теплообменных аппаратов производится по проходному сечению трубного пространства / 3, табл. 2.3 /.
4.3.3. Параметры подогревателя необходимые для уточнённого расчёта.
Подача горячего теплоносителя - в межтрубное пространство
Направление потоков – противоток
Расположение аппарата - горизонтальное
Расположение труб – шахматное
Наличие перегородок – есть
Аппарат шестиходовой
| Внутренний диаметр кожуха – D,мм | 600 |
| Внутренний диаметр труб – d,мм | 16 мм |
| Толщина стенки труб – d,мм | 2 мм |
| Проходное сечение трубного пространства м2 | 0,9*10-2 |
| Проходное сечение межтрубного пространства – Sм102 м2 | 4,8*10-2 |
| Теплопроводность материала труб – l | 46,5 Вт/(мК) |
| Число труб n | 316 |
| Число ходов Z | 6 |
| Число рядов труб nр | 18 |
.
5. Подробный расчет теплообменного аппарата
5.1 Теплоотдача в трубах
По (/1/, табл. 4.1, стр. 151) находим, что теплоотдача для раствора
где
Коэффициент
где
По формуле 3.7 плотность раствора при
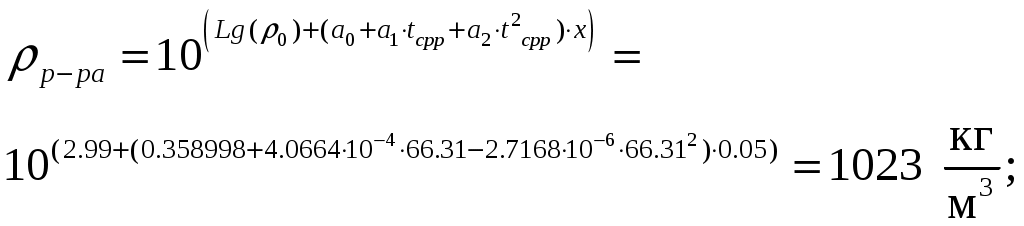
Среднюю скорость потока определяем по формуле:
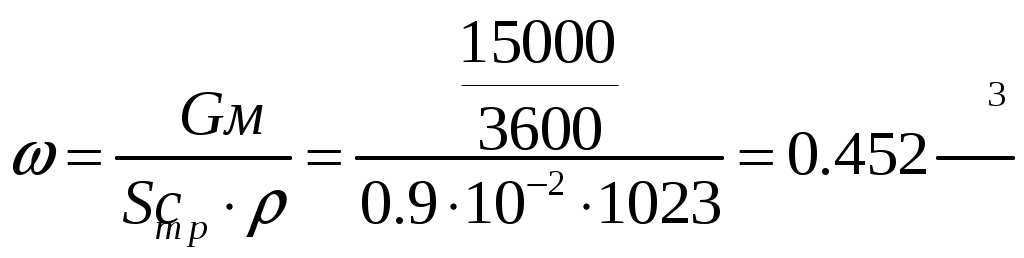
Учитывая, что для труб круглого сечения диаметр труб и эквивалентный диаметр совпадают, то для труб
Критерий Прандтля находим по формуле:
где
Коэффициент теплопроводности при
Таким образом, критерий Pr при
Коэффициент теплоотдачи от раствора к стенке:
С учетом формулы 3.25 получаем:
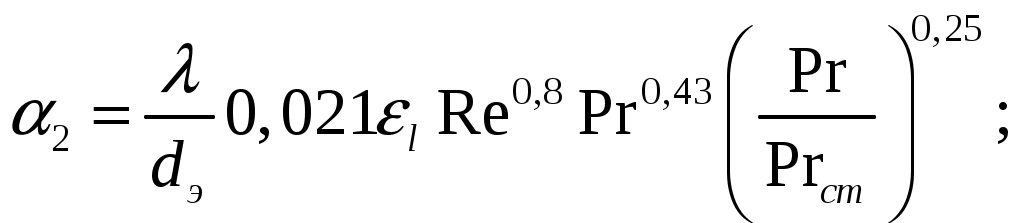
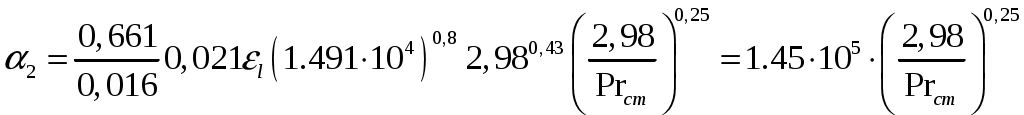
5.2 Теплоотдача при пленочной конденсации водяного пара
Для водяного пара в случае конденсации на пучке горизонтальных труб осредненный по всему пучку коэффициент теплопередачи
где
Поправочный множитель
Имеем:
5.2.1 Расчет коэффициента теплопередачи
Первое приближение.
Принимаем в первом приближении
Тогда по формуле (3.29) получаем:
При этом удельный тепловой поток от пара к стенке равен:
Сумма термических сопротивлений равна:
где
По (/1/, табл. XXXI, стр. 531) находим:
Для стенки:
где
Поскольку удельный тепловой поток от пара к стенке
при этом
При температуре
Подставляя найденные значения в формулу 3.27, получаем значение критерия Прандтля при температуре стенки:
По формуле 3.28 находим в коэффициент теплоотдачи от раствора к стенке: