Файл: Задач Найти остаток от деления многочлена 2x 5 x 4 6x 2 5x на многочлен x 1.docx
Добавлен: 11.01.2024
Просмотров: 43
Скачиваний: 4
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
Итоговая контрольная работа
Задача1. Найти остаток от деления многочлена 2x5 + x4 - 6x2 + 5x на многочлен x – 1
Ответ: Делим первый элемент делимого на старший элемент делителя, помещаем результат под чертой:
| 2x5 + x4 - 6x2 + 5x | x - 1 |
| 2x5 - 2x4 | 2x4 |
| 3x4 - 6x2 + 5x | |
| 2x5 + x4 - 6x2 + 5x | x - 1 |
| 2x5 - 2x4 | 2x4 + 3x3 |
| 3x4 - 6x2 + 5x | |
| 3x4 - 3x3 | |
| 3x3 - 6x2 + 5x | |
| 2x5 + x4 - 6x2 + 5x | x - 1 |
| 2x5 - 2x4 | 2x4 + 3x3 + 3x2 |
| 3x4 - 6x2 + 5x | |
| 3x4 - 3x3 | |
| 3x3 - 6x2 + 5x | |
| 3x3 - 3x2 | |
| - 3x2 + 5x | |
| 2x5 + x4 - 6x2 + 5x | x - 1 |
| 2x5 - 2x4 | 2x4 + 3x3 + 3x2 - 3x |
| 3x4 - 6x2 + 5x | |
| 3x4 - 3x3 | |
| 3x3 - 6x2 + 5x | |
| 3x3 - 3x2 | |
| - 3x2 + 5x | |
| - 3x2 + 3x | |
| 2x | |
| 2x5 + x4 - 6x2 + 5x | x - 1 |
| 2x5 - 2x4 | 2x4 + 3x3 + 3x2 - 3x + 2 |
| 3x4 - 6x2 + 5x | |
| 3x4 - 3x3 | |
| 3x3 - 6x2 + 5x | |
| 3x3 - 3x2 | |
| - 3x2 + 5x | |
| - 3x2 + 3x | |
| 2x | |
| 2x - 2 | |
| 2 | |
Ответ: Остаток = 2
Задача 2. Используя формулы Муавра найти все корни
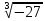, и записать их в алгебраической форме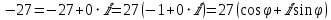
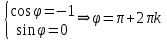
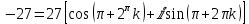
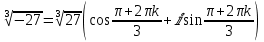. Берём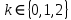 
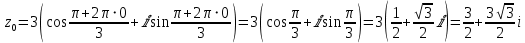
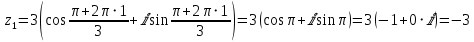
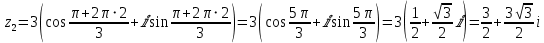
При этом
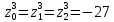
Задача 3. Найти матрицу, обратную матрице
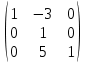
Ответ: Для вычисления обратной матрицы запишем данную матрицу, дописав к ней справа единичную матрицу:
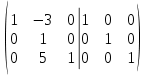
Теперь, что бы найти обратную матрицу, используя элементарные преобразования над строками матрицы, преобразуем левую часть полученной матрицы в единичную. К 1
строке добавляем вторую строку, умноженную на 3, от 3 строки отнимаем вторую строку, умноженную на 5:
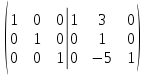
Ответ:
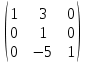
Задача 4. Найти каноническое уравнение прямой, проходящей через точку A(1, 2, 3) и перпендикулярную плоскости с общим уравнением 5x – 3y – 12z – 7 = 0
Ответ : Общее уравнение плоскости имеет вид:
Ax+By+Cz+D=0
где n(A,B,C)− называется нормальным вектором плоскости.
Уравнение прямой, проходящей через точку
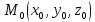и имеющий направляющий вектор q(l, m, n) имеет следующий вид: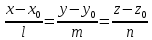
Для того, чтобы прямая была ортогональна плоскости, направляющий вектор q(l, m, n) прямой должен быть коллинеарным нормальному вектору n(A,B,C) плоскости. Следовательно, в качестве направляющего вектора прямой можно взять нормальный вектор плоскости
Таким образом, уравнение прямой, проходящей через точку
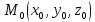и ортогональный плоскости имеет следующий вид: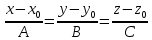
Подставляя координаты точки и координаты нормального вектора плоскости в (3), получим:
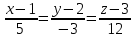
Ответ: Каноническое уравнение прямой:
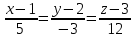
Задача 5. Решить СЛАУ
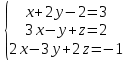
Ответ : Перепишем систему уравнений в матричном виде и решим методом Гаусса:
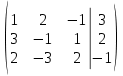
От 2 строки отнимаем 1 строку, умноженную на 3. От 3 строки отнимаем 1 строку, умноженную на 2:
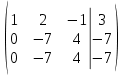
2 строку делим на -7:
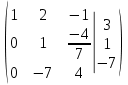
От 1 строки отнимаем 2 строку, умноженную на 2. К 3 строке добавляем 2 строку, умноженную на 7:
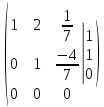
Ответ: Система имеет множество решений:
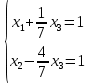
Задача 6. Найти канонический вид квадратичной формы
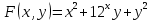
Ответ : Выпишем матрицу квадратичной формы:
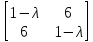= 0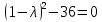
; 
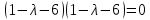
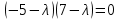
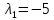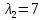
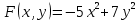
Ответ:
