Файл: Решение. Событие а сумма выпавших очков меньше пяти. По классическому определению вероятности.doc
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 11.01.2024
Просмотров: 44
Скачиваний: 1
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
Задание 1.
Игральная кость подброшена дважды. Определить вероятность того, что сумма выпавших очков меньше пяти.
Решение.
Событие А – сумма выпавших очков меньше пяти.
По классическому определению вероятности,
Число всевозможных комбинаций выпадения очков при двукратном бросании игральной кости:
Найдем число исходов, при которых сумма выпавших очков меньше пяти: 1+1, 1+2, 2+1, 2+2, 1+3, 3+1, тогда число благоприятных исходов:
Найдем искомую вероятность:
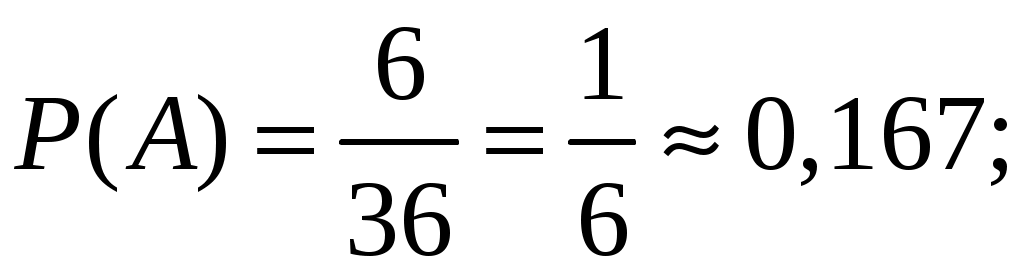
Задание 2.
В цветочном киоске имеются восемь роз и восемь хризантем. Определить вероятность того, что наудачу составленный букет из пяти цветов будет состоять из цветов одного вида.
Решение.
Событие А – наудачу составленный букет из пяти цветов состоит из из цветов одного вида.
Для удобства кратко запишем условия опыта.
Всего цветов – 8+8=16; выемка – 5.
Число всевозможных исходов выемки 5-ти цветов из 18-ти равно:
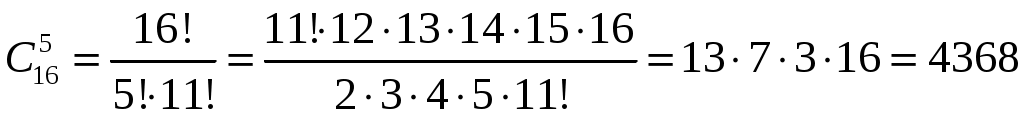 .
.Число способов выемки пяти роз из 8-ми или пяти хризантем из 8-ми равно:
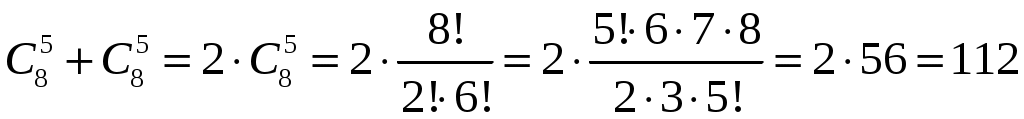 .
.Найдем искомую вероятность:
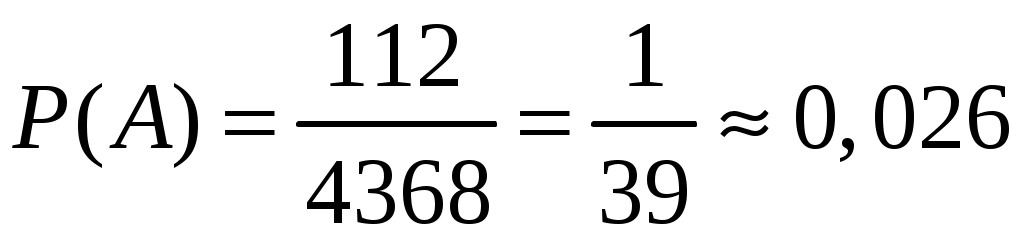 .
.Задание 3.
В цехе три станка изготовляют детали. Первый станок выпускает 40% всей продукции, второй – 25% и третий – 35%. Вероятность появления брака на первом станке – 0,02, на втором – 0,01, на третьем – 0,03. Найти процент брака в изделиях, выпущенных всем цехом.
Решение.
Событие А – выпущена бракованная деталь.
При взятии детали наугад рассмотрим три гипотезы:
- наугад взятая деталь выпущена вторым станком,
Очевидно, что события
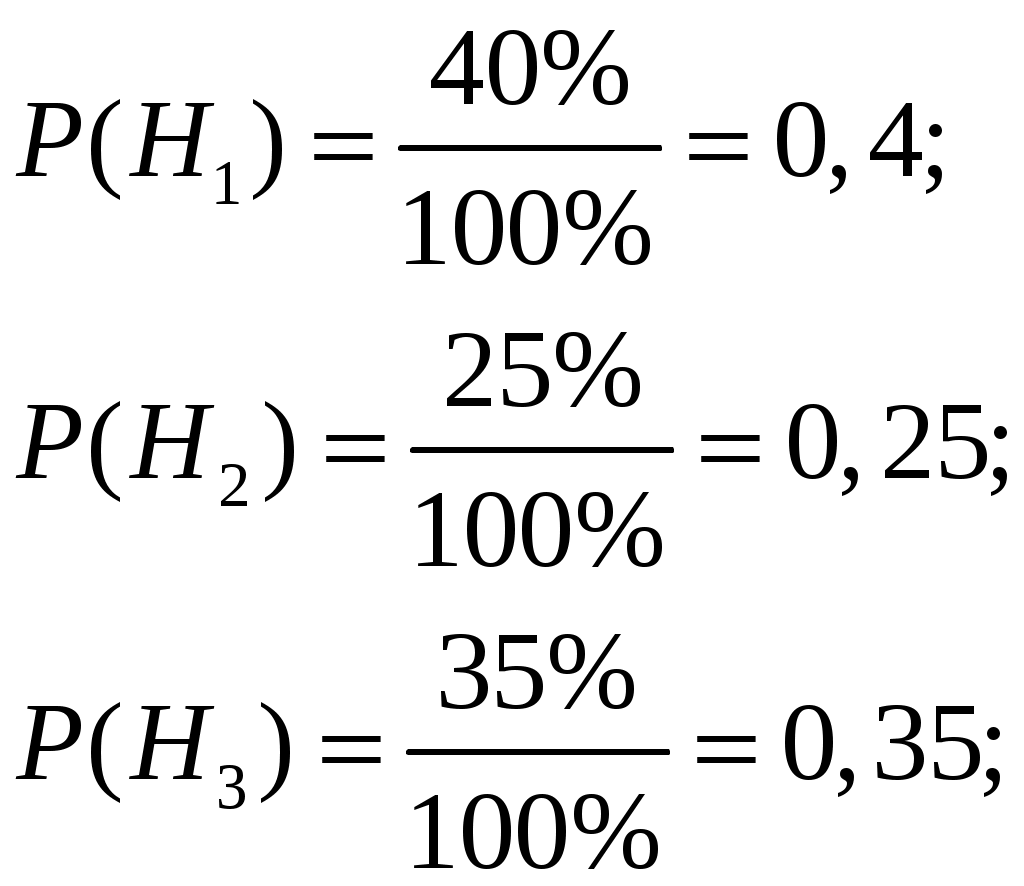
Контроль:
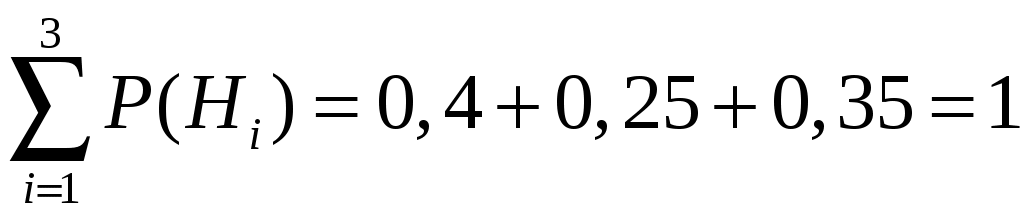 .
.Определим условные вероятности события А:
Тогда, по формуле полной вероятности, вероятность того, взятая деталь будет бракованной равна:
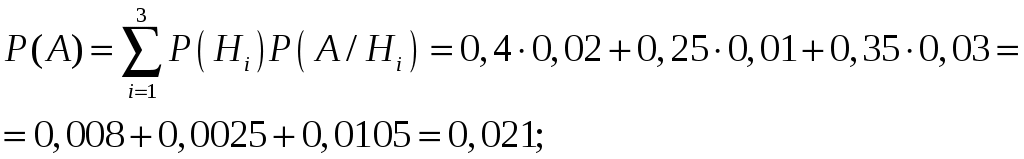
Тогда общий процент брака равен
Задание 4.
Стрелок ведет стрельбу до первого попадания, имея боезапас пять патронов. Вероятность попадания при каждом выстреле равна 0,6. Составить закон распределения случайной величины – возможного числа использованных патронов. Найти математическое ожидание, дисперсию, среднее квадратическое отклонение и моду случайной величины. Записать функцию распределения
Решение.
Определим случайную величину
Рассмотрим возможные варианты значений случайной величины в порядке возрастания.
Определим вероятность попадания при каждом выстреле
1) Использован только один патрон, т.е. 1-ый выстрел попал в мишень, тогда
2) Израсходовано два патрона, т.е. первый выстрел не попал в цель, а второй выстрел попал в цель, тогда
3) Израсходовано три патрона, т.е. первые два выстрела не попали в цель, а третий выстрел попал в цель, тогда
4) Израсходовано четыре патрона, т.е. первые три выстрела не попали в цель, а 4-ый выстрел попал в цель, тогда
5) Израсходовано пять патронов, т.е. первые четыре выстрела не попали в цель и уже не важно, попал ли в цель пятый выстрел, тогда
Составим ряд распределения возможного числа использованных патронов из пяти имеющихся:
| | 1 | 2 | 3 | 4 | 5 |
| | 0,6 | 0,24 | 0,06 | 0,0384 | 0,0256 |
1. Проверим правильность заполнения дискретного ряда:
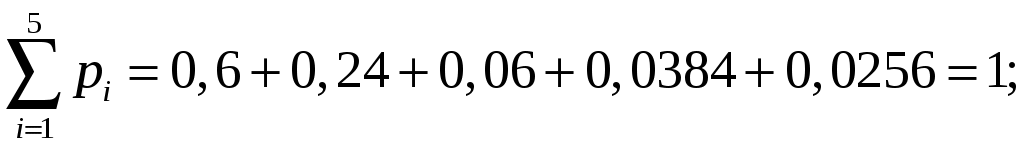 .
.2. Математическое ожидание числа использованных патронов.
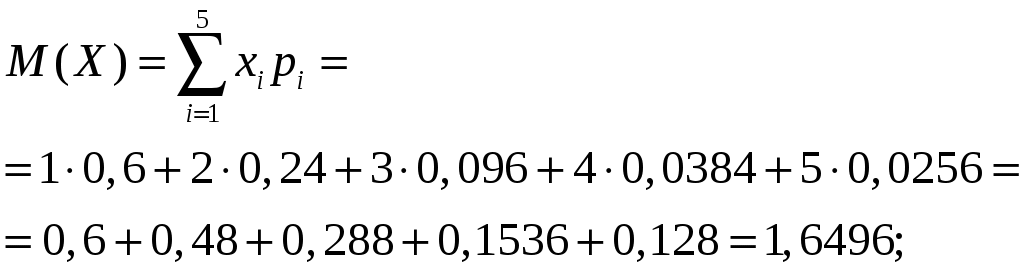 .
.3. Дисперсия случайной величины
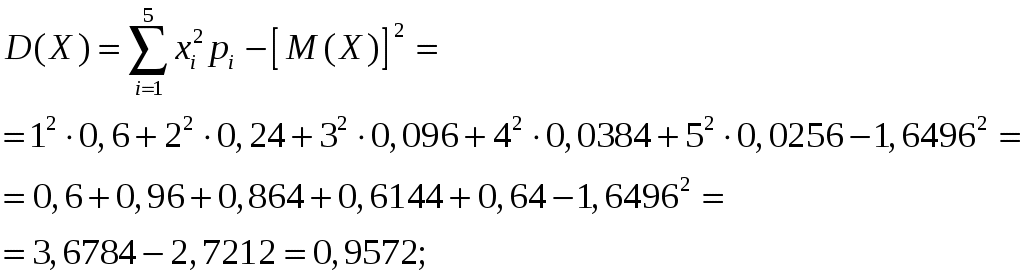
4. Среднее квадратическое отклонение величины
5. Мода – значение случайной величины, имеющей наибольшую вероятность. В данном распределении
6. Найдем функцию распределения.
По определению функция распределения случайной величины
Найдем значения
1)
2)
3)
4)
5)
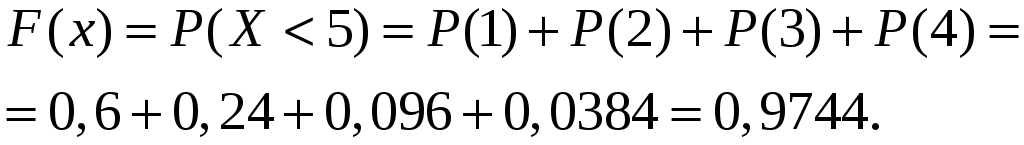
6)
Запишем функцию распределения:
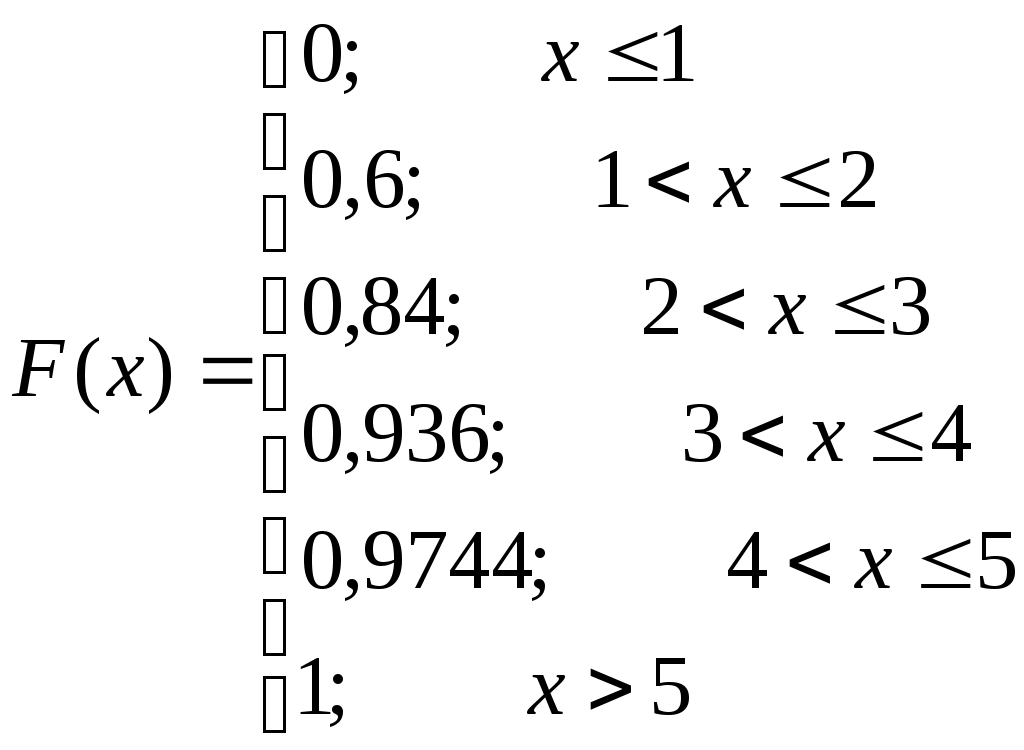
График функции распределения:
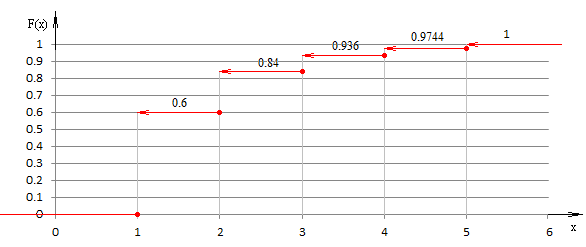
Задание 5.
Случайная величина
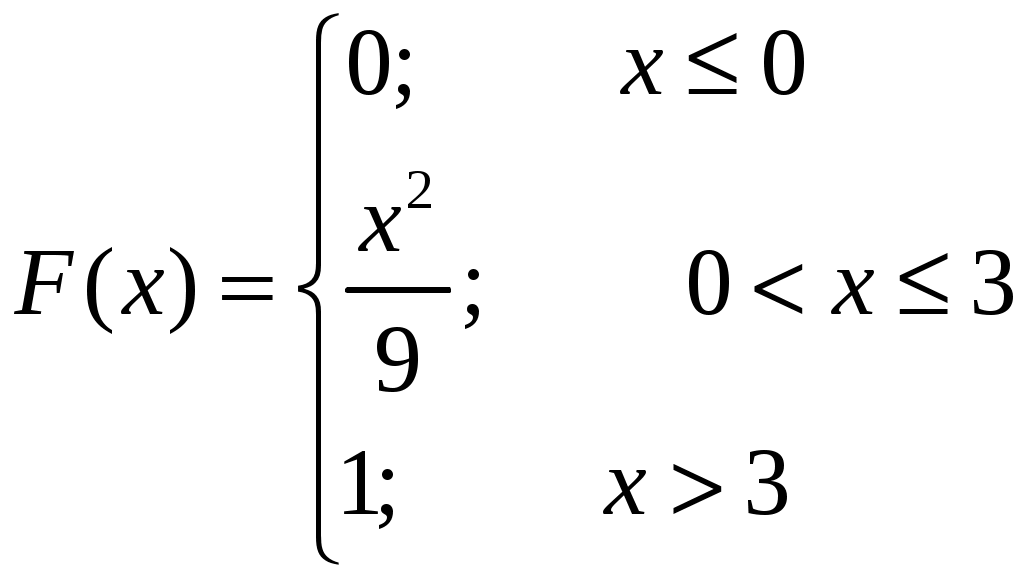
Решение.
1. По определению плотность распределения непрерывной случайной величины равна производной от функции распределения
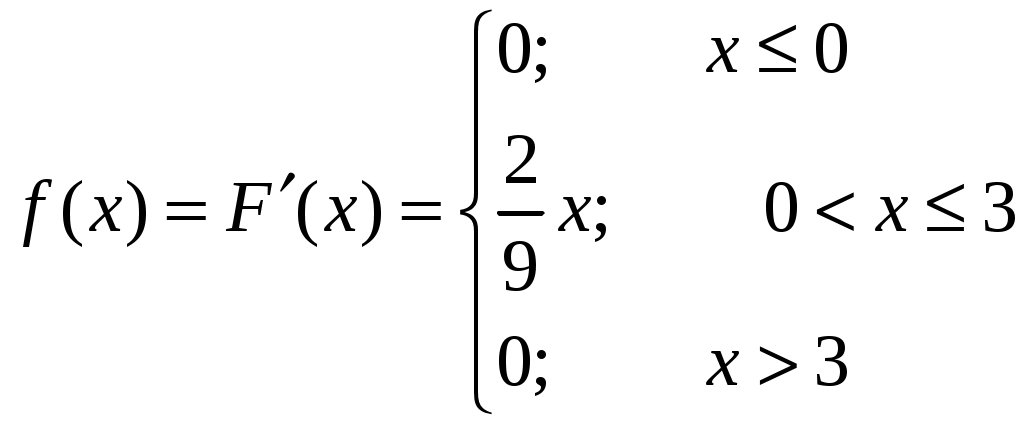
2. Математическое ожидание случайной величины:
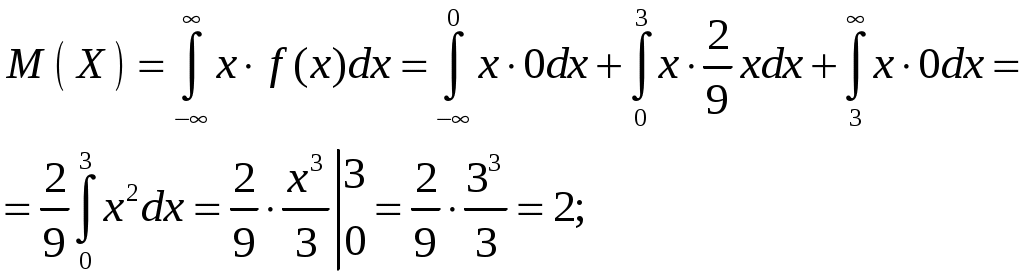
3. Дисперсия случайной величины:
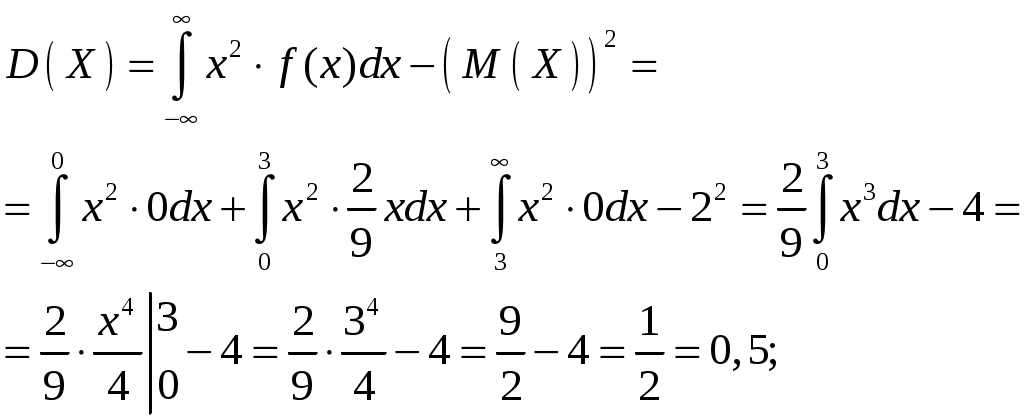
4. Среднее квадратическое отклонение величины
5. Вероятность попадания случайной величины в интервал
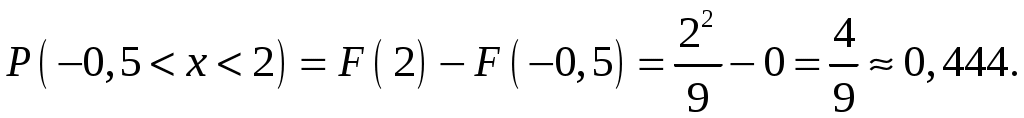
6. Построим графики функции распределения ‒