Контрольная работа«Статистика (теория статистики, социально-экономическая статистика)»Задача 1Имеются следующие данные за год по заводам одной промышленной компании:Таблица 1

Завод	Среднее число рабочих, чел.	Основные фонды, млн руб.	Продукция, млн руб.	Завод	Среднее число рабочих, чел.	Основные фонды, млн руб.	Продукция, млн руб.
1	700	250	300	9	1400	1000	1600
2	800	300	360	10	1490	1250	1800
3	750	280	320	II	1600	1600	2250
4	900	400	600	12	1550	1500	2100
5	980	500	800	13	1800	1900	2700
6	1200	750	1250	14	1700	1750	2500
7	1100	700	1000	15	1900	2100	3000
8	1300	900	1500

---

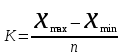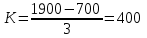
На основании приведенных данных составьте групповую таблицу зависимости выработки на одного рабочего от величины заводов по числу рабочих. Число групп – три.Решение:Величину интервала рассчитаем по формуле: , (1)где х_max, x_min – максимальное и минимальное значения объема продукцииn – количество группОбозначим границы групп:группа граница1-ая 700 – 11002-ая 1101 – 15003-я 1501 – 1900Рассчитаем необходимые показатели по каждой группе (таблица):Разработочная таблица группировки заводов по среднему числу рабочихТаблица 2

Группы заводов по числу рабочих	Завод	Среднее число рабочих, чел.	Основные фонды, млн руб.	Продукция, млн руб.
700 - 1100	1	700	250	300
	3	750	280	320
	2	800	300	360
	4	900	400	600
	5	980	500	800
	7	1100	700	1000
Итого	6	5230	2430	3380
1101-1500	6	1200	750	1250
	8	1300	900	1500
	9	1400	1000	1600
	10	1490	1250	1800
Итого	4	5390	3900	6150
1501-1900	12	1550	1500	2100
	11	1600	1600	2250
	14	1700	1750	2500
	13	1800	1900	2700
	15	1900	2100	3000
Итого	5	8550	8850	12550

---

Представим результаты группировки в таблице:Таблица 3. Аналитическая группировка заводов по числу рабочих

№ п/п	Ширина интервала	Кол-во заводов в группе	Число рабочих, чел.	Продукция, млн. руб.	Продукция на 1 рабочего, млн. руб.
1	700-1100	6	5 230	3380	0.646
2	1101-1500	4	5 390	6150	1.141
3	1501-1900	5	8 550	12550	1.468
Итого:		15	19170	22080	1.152

Задача 2Планом промышленного предприятия предусматривалось снижение затрат на 1 рубль товарной продукции на 4%, фактически затраты возросли на 2%. Вычислите относительную величину выполнения плана.РешениеОтносительная величина выполнения плана (ОВВП) определяется отношением относительной величины динамики затрат (ОВД) к относительной величине планового задания (ОВПЗ).ОВПЗ = 1-0,04 = 0,96, т.к. планировалось снизить затраты на 4%ОВД = 1 + 0,02 = 1,02, т.к. фактически затраты возросли на 2%.ОВВП = ОВД / ОВПЗ = 1,02 / 0,96 = 1,06т.е. план перевыполнен на 6%.Задача 3Вычислите среднемесячный процент брака по заводу за второй квартал по следующим данным:Таблица 4

Показатель	апрель	май	июнь
Выпуск годной продукции, тыс. руб.	5000	6000	6500
Брак, в % к годной продукции	1,5	1,2	1,0

РешениеОпределим среднемесячный процент брака по формуле средней арифметической взвешенной

---

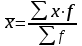
, (2)
Необходимые расчеты проведем в таблице:
Таблица 5

Показатель	Брак, в % к годной продукции	Выпуск годной продукции, тыс.руб.	Брак, тыс.руб.
	х	f	xf
апрель	1.5	5000	75
май	1.2	6000	72
июнь	1.0	6500	65
Итого:	х	17500	212

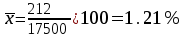- среднемесячный процент брака по заводу за второй кварталЗадача 4Определите среднюю выработку рабочего за смену и среднеквадратическое отклонение, моду и медиану, используя следующие данные:Таблица 6

Выработано деталей рабочим в смену, шт.	23	20	32	24
Число рабочих с данной выработкой, чел.	38	18	10	34

РешениеДля исчисления необходимых показателей проведем следующие расчеты:Таблица 7

Выработка 1 рабочего, x	Число рабочих, f	x * f	S	(x - x ср) * f	(x - x ср)2 * f
20	18	360	18	-66.6	246.42
23	38	874	56	-26.6	18.62
24	34	816	90	10.2	3.06
32	10	320	100	83.0	688.90
Итого:	100	2370	-	0	957.00

---

1. Средняя выработка рабочего в смену:, (3) 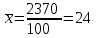шт.2. Мода - это признак, на который приходится наибольшее количество частот. В данном случае модальной является выработка 1 рабочего - 23 шт. в смену, т.к. число рабочих с данной выработкой составляет 38% (38 чел. из 100).3. Медиана 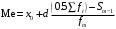, (4)где 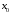– нижняя граница медианного интервала; 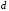– величина медианного интервала; 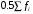– полусумма частот всех интервалов; 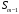– сумма частот до медианного интервала; 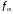– частота медианного интервала.Медианным является серединное значение - 23 шт., это значит, что 50% рабочих совокупности вырабатывают не более 23шт. в смену, остальные 50% - более 23шт. 4. Среднее квадратическое отклонение 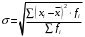, (5)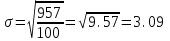Задача 5По приведенным данным о выпуске продукции химическим предприятием по годам в сопоставимых ценах вычислить на постоянной и переменной базах сравнения абсолютный прирост, темпы роста и прироста, а также абсолютное значение 1 % прироста. Рассчитать средний уровень ряда. Рассчитать при помощи метода скользящей средней за каждые три года среднегодовой выпуск продукции. Произвести аналитическое выравнивание ряда по прямой.Таблица 8

Годы	1995	1996	1997	1998	2000	2001
Выпуск продукции, млн руб.	40	50	60	66	79,2	110,8

Решение

1. 
   Абсолютный прирост - характеризует размер увеличения или уменьшения изучаемого явления за определенный период времени. Он определяется как разность между данным уровнем и предыдущим (цепной) или первоначальным (базисный);
   
2. 
   Коэффициент роста – равен отношению последующего уровня к предыдущему (цепной) или первоначальному ( базисный);
   
3. 
   Темп прироста – показывает относительную величину прироста, т.е. на сколько процентов сравниваемый уровень больше или меньше предыдущего уровня (цепной) или уровня, принятого за базу сравнения (базисный);
   
4. 
   Абсолютное значение 1% прироста – исчисляется как отношение абсолютного прироста к соответствующему темпу прироста, отражает значимость каждого процента прироста.
   

---

Смотрите также файлы

• Реферат аудит готовой продукции студент группы 338бс1 Олимова Алика Комиловна Тверь, 2023.docx

• Практическая работа Задание для практической работы по.docx

• Ученые записки университета имени пф. Лесгафта 2015. 7 (125).pdf

• Рассказало о подвигах бойцов во время спецоперации на Украине.docx

• Жарыты шаылуы. Шаылу задары. Жазы айна.doc