В формуле аддитивной оценки вероятности суммы сообщения P(…)<=…P(A) равенство имеет место, если сообщения A1, A2, … , An несовместные

Вероятность сообщения A+B равна P(A) + P(B) – P(AB)

Вероятность сообщения A равна 1-P(A)

В теоретико-информационных исследованиях для вычисления значения собственной информации используют формулу I(x)=-ln p(x)



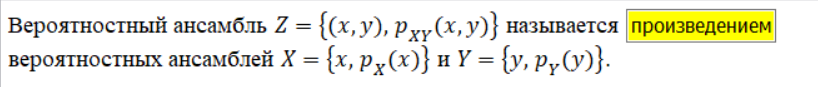Возникновение научного направления «Теория информации»…работы «Математическая теория связи»



Вероятностные ансамбли X и Y, распределения вероятностей на которых связаны соотношением p(x, y) = p(x)p(y), xX, yY, называются независимыми

Вероятность пустого сообщения равна 0

В формуле аддитивной оценки вероятности суммы сообщений … равенство имеет место в случае, если сообщения A1, A2, …, An несовместные

Всем интуитивным к информационной мере удовлетворяет логарифмическая функция

Дисперсия D(x+y) равна сумме D(x)+D(y)дисперсий для некоррелированных случайных величин

Длина сообщения A в теории информации обозначается |A|

Дискретное множество X сообщений называется полным сообщением

Для любой случайной величины xX и для любой числовой константы cR математическое ожидание M(cx) равно cM(x)

Для любой случайной величины xX и для любой числовой константы cR дисперсия D(c+x) равна D(x)

Для любой случайной величины xX и для любой числовой константы cR дисперсия D(cx) равна c^2D(x)

Для любой числовой константы cR математическое ожидание равно c

Для любой числовой константы cR дисперсия равна 0

Для любого сообщения xX I(x)>=0

Для любых независимых сообщений x1, x2, …, xn : I(x1, x2, …, xn) = I(x1)+ I(x2)+…+ I(xn)

Для любого дискретного вероятностного ансамбля H(X) >= 0

Если p(x1)>=p(x2), то I(x1) <= I(x2) для любых сообщений

Информационная мера должна удовлетворять требованию µ(p^m) = mµ(p)

Информационная мера должна однозначно определяться вероятностью сообщения

Информационная мера по знаку должна быть неотрицательной величиной

Информационная мера для независимых сообщений должна быть равна сумме мер отдельных сообщений

Количество элементарных сообщений xA, из которых составлено сообщение A, называется длиной сообщения A

---

Множество X сообщений в совокупности с распределением вероятностей {p(x) : xX } называется дискретным вероятностным ансамблем

Математическое ожидание M(x+y) равно сумме M(x)+M(y) математических ожиданий для любых случайных величин xX и yY

Математическое ожидание M(xy) равно произведению M(x)M(y) математических ожиданий для независимых случайных величин xX и yY

Множество Z, определяемое равенством Z = {(x,y): xX и yY }, называется произведением множества X и Y



Операция над сообщением AX, которая определяется выражением { xX : x!=A} называется дополнением

Операция над сообщениями A,BX, которая определяется выражением {xX:A или xB}, называется суммой

При практическом решении задач теории информации для вычисления собственной значения информации используют формулу I(x) = -log2 p(x)

При вычислении значения собственной информации по формуле I(x) = -ln p(x) единицей измерения является нат

При вычислении значения собственной информации по формуле I(x) = -lg p(x) единицей измерения является хартли

При вычислении значения собственной информации по формуле I(x) = -log2 p(x) единицей измерения является бит

Произвольный элемент xX конечного или счетного множества X в теории информации называется элементарным сообщением

Произвольное непустое подмножество AX конечного или счетного множества X в теории информации называется сообщением

Раздел теории информации, в котором рассматриваются методы кодирования, обеспечивающие наилучший компромисс между качеством информации и затратами на ее передачу, называется кодированием информации с заданным критерием качества

Раздел теории информации, в котором рассматриваются кодирование без потерь, кодирование для канала связи без шума и сжатие информации, называется кодированием дискретных источников информации

Раздел теории информации, в котором рассматриваются методы защиты информации от помех в каналах связи, называется кодированием информации для передачи по каналу связи с шумом

Раздел теории информации, в котором рассматриваются вопросы защиты информации от несанкционированного доступа, называется секретной связью

---

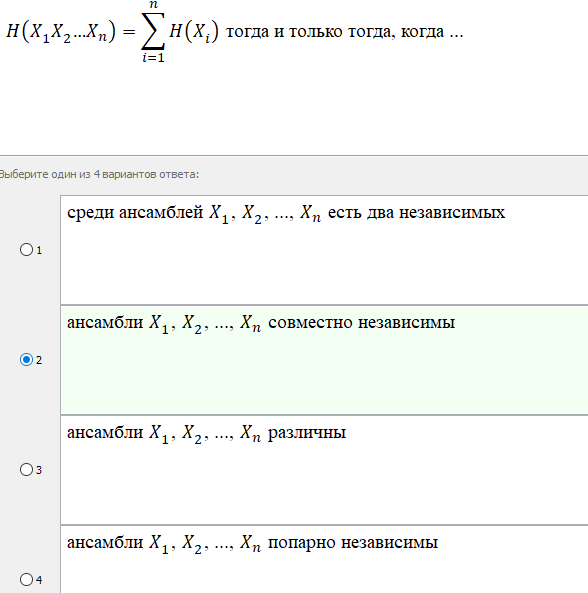
Сообщения A1, A2, …, AnX которые связаны соотношением P(A1A2...An)= P(A1)P(A2)…P(An), называются совместно независимыми

Сообщения A и B, для которых выполнено равенство AB!=0, называются несовместными

Сообщение А в теории информации называется сложным, если |A|>1

Сообщения A,BX, которые связаны соотношением P(AB) + P(A) P(B), называются независимыми

Собственная информация элементарного сообщения x, выбираемого из вероятностного ансамбля X={x, p(x)}, называется величина, определяемая по формуле I=-log p(x)

Сообщение A, которое имеет длину |A| = 0, называется пустым

Теория информации как научное направление оформилось в 1948 году

Терминология в теории информации заимствована, в основном, из теории вероятностей

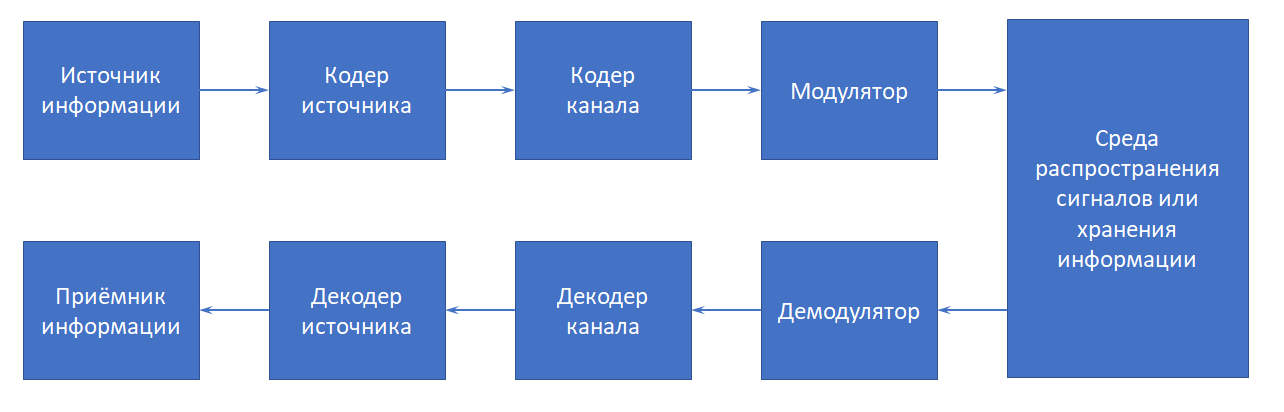
Устройство или объект живой природы, порождающий сообщения, которые должны быть перемещены в пространстве или во времени, называется источником информации

Устройство или объект живой природы, которому адресованы сообщения, сформированные источником информации, называется приёмником информации

Устройство, которое осуществляет представление информации в наиболее компактной форме с целью максимально эффективно использовать ресурсов канала связи или запоминающего устройства, называется кодером источника

Устройство, которое используется для преобразования сообщений, сформированных декодером канала, в сообщения … приемник информации, называется декодером источника

Устройство, которое используется для преобразования сообщений, сформированных демодулятором, в сообщения кодером источника, называется декодером канала

Укажите для каких случайных величин xX и yY корреляционный момент K(x,y)равен нулю

Для некоррелированных

Для независимых

Устройство, которое выполняет обработку информации с целью защиты сообщений от помех при передачи по каналу связи либо от возможных искажений при хранении информации, называется кодером слова

---

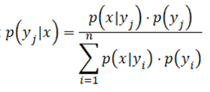
Формула апостериорной вероятности

Формула Байеса



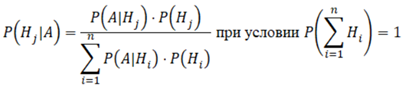
Формула апостериорной вероятности

Формула Байеса

Устройство или объект живой природы, которому адресованы сообщения, сформированные источником информации, называется приёмником информации



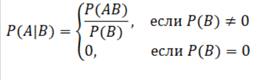
Устройство, которое используется для преобразования сигналов, согласованных с физической природой канала связи или средой накопителя информации, в сообщениях, которые были сформированы кодером канала, называется демодулятором



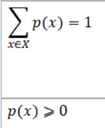
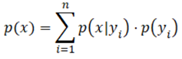называется формулой полной вероятности

корреляционным моментом

формулой умножения вероятностей

дисперсией

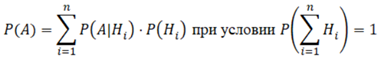формулой полной вероятности

---

Смотрите также файлы

• Что такое гомогаметный и гетерогаметный пол.docx

• Автономной некоммерческой образовательной организации высшего образования центросоюза российской федерации.docx

• Введение глава пародонт и его особенности.docx

• Они сражались за Родину.docx

• Безличные глаголы. Развитие навыков пользования лингвистическими словарями различных типов.doc