СОДЕРЖАНИЕ

Введение 3

1. 
   Теоретическая часть 5
   
2. 
   Практическая часть 9
   

Заключение 13

ВВЕДЕНИЕ

Согласно определению, модель – это объект-заменитель объекта-оригинала, наделенный некоторыми его свойствами в соответствии с целями моделирования. В настоящее время термин "модель" используется в самых различных сферах человеческой деятельности. Если рассматривать модель с точки зрения экономических наук, то это некоторый образ реального объекта в математической или идеальной форме, отражающий существенные свойства моделируемого объекта и замещающий его в исследовании и управлении.

Следует отметить, что существуют модели разных видов: физические, графические, математические, описательные, абстрактные. Особое место в науке занимают математические модели, записанные с помощью математических и логических символов и операторов. Они основываются на математическом описании объекта, в него входят взаимосвязи параметров объекта, что характеризует его особенности функционирования. Математическую модель экономического процесса или явления более кратко можно назвать экономико-математической моделью объекта, которая является его отображением в виде совокупности уравнений, неравенств, формул, логических отношений, графиков.

Из вышесказанного следует, что моделирование – это процесс создания моделей, исследования по ней какого-либо объекта, процесса или явления. Метод моделирования основывается на методе аналогий, то есть возможности изучения реального объекта (почему-либо трудно доступного для исследований) не непосредственно, а через рассмотрение подобного ему и более доступного. При построении моделей те или иные теории или гипотезы становятся обозримыми, уточняются, и это способствует лучшему пониманию изучаемых проблем. 

Экономико-математическое моделирование является неотъемлемой частью любого исследования в области экономики. К его задачам относятся прогнозирование, оптимизация и управление. Существует множество методов экономико-математического моделирования. Основным является аппроксимация функций.

Целью выполнения практической работы является изучение механизмов аппроксимации функций методом наименьших квадратов, закрепление навыков работы с этим методом.

Для достижения цели были поставлены следующие задачи:

---

1. 
   Используя метод наименьших квадратов, аппроксимировать функцию
   
2. 
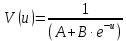
   Сравнить исходные значения с рассчитанными;
   
3. 
   Сделать выводы.
   

1. 
   Теоретическая часть
   

Аппроксимацией функции ????(????) называется подбор функции ????(х), максимально приближенной к зависимости в исходных данных. Аппроксимация позволяет исследовать количественные характеристики объекта, сводя задачу к изучению более простых или более удобных объектов.

Основным объектом исследования, как правило, является выборка экспериментальных данных, которая, чаще всего, представляется в виде массива, состоящего из пар чисел ( 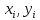). В связи с этим возникает задача аппроксимации конкретной зависимости y( 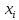) непрерывной функцией ????(х). Функция ????(х), в зависимости от специфики задачи, может отвечать различным требованиям:

1. Функция ????(х) должна проходить через точки ( 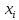, 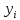), т. е. ????( 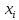)= 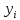, ????=1...????. В этом случае говорят об интерполяции данных функцией ????(????) во внутренних точках между ????????, или экстраполяции за пределами интервала, содержащего все .

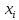2. Функция ????(х) должна некоторым образом (например, в виде определенной аналитической зависимости) приближать ????( 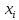), не обязательно проходя через точки ( 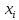, 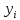). Такова постановка задачи регрессии, которую во многих случаях также можно назвать сглаживанием данных.

3. Функция ????(х) должна приближать экспериментальную зависимость ????(

---

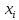
), учитывая, к тому же, что данные ( , ) получены с некоторой погрешностью. При этом функция ????(х), с помощью того или иного алгоритма уменьшает погрешность, присутствующую в данных ( , ). Такого типа задачи называют задачами фильтрации.

Существует множество методов аппроксимации. Наиболее распространенные из них:

1. Метод интерполяции

=????( ), ????=0,1…, ????, ????≤ ≤????.

Задача интерполяции – найти функцию ????(х), принимающую в точках те же значения . Тогда условие интерполяции можно представить в виде:

????( )= .

Задача нахождения интерполяционной функции ????(х) имеет много решений, так как через заданные точки , можно провести бесконечно много кривых, каждая из которых будет графиком функции, для которой выполнены все условия интерполяции. Для практики важен случай интерполяции функции многочленами:



при этом искомый полином называется интерполяционным полиномом.

2. Метод Лагранжа

Интерполяционный полином Лагранжа — многочлен минимальной степени, принимающий данные значения в данном наборе точек. Для ????+1 пар чисел (????0, ????0), (????1, ????1) … (????????, ????????), где все ???????? различны, существует единственный многочлен ????(????) степени не более ????, для которого ????(????????)= ????????.

Интерполяционный полином Лагранжа имеет вид:

---

3. Метод Ньютона

Это численный метод нахождения корня (нуля) заданной функции. Поиск решения осуществляется путём построения последовательных приближений. Разделенные разности нулевого порядка совпадают со значениями функции в узлах. Разделенные разности первого порядка определяются через разделенные разности нулевого порядка:



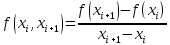
4. Метод Тейлора

Это ряд Тейлора по одной точке и многим производным в ней:



Считается, что чем больше членов этого ряда, тем точнее аппроксимация, тем точнее найденный приближенный корень аппроксимации к реальному корню функции.

В результате, чтобы аппроксимировать кривую (комбинацию точек) в ряд Тейлора, необходимо, согласно приведенной формуле, знать не ряд точек, а ряд производных в этой точке.

5. Метод наименьших квадратов

Это наиболее распространенный метод аппроксимации экспериментальных данных. Метод позволяет использовать аппроксимирующие функции произвольного вида и относится к группе глобальных методов.

Простейшим вариантом метода наименьших квадратов является аппроксимация прямой линией. Критерием близости при использовании метода наименьших квадратов является требование минимальности суммы квадратов отклонений от аппроксимирующей функции до экспериментальных точек. Для аппроксимации функции методом наименьших квадратов существует следующая формула 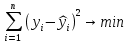(1):

. (1)

где n - число экспериментальных результатов  .

Для нахождения минимума потребуется продифференцировать функцию, тем самым составив систему уравнений:



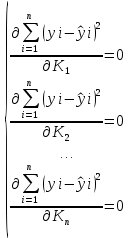
где K1, 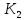…, 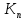– искомые для математической модели коэффициенты, а 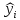– данная для аппроксимации функция.

Далее раскрываем скобки и приравниваем частные производные к нулю, приводим уравнения к стандартному виду (сумма произведений переменных и их коэффициентов равняется некоторому числу),
записываем СЛАУ в матричном виде и решаем любым удобным способом, подставляем полученные коэффициенты в подобранную функцию. Затем считаем

---

????????̂ для каждой переменной. Строим график.
Оцениваем верность подобранной функции и делаем вывод.

2. 
   Практическая часть
   

Используя метод наименьших квадратов, необходимо найти аппроксимирующую функцию по исходным данным из следующей таблицы (таблица 1), построить графики исходной и полученной функции и сравнить их.



Таблица 1 ̶ Исходные данные

u	2	2,5	3	3,5	4	4,5	5	5,5	6
V(u)	5,197	7,78	11,14	15,09	19,24	23,11	26,25	28,6	30,3

Применим формулу для аппроксимации функции методом наименьших квадратов, целевая функция будет иметь вид:

Решение. Для удобства введем замену: z= 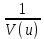и w=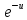 , соответственно получаем следующую функцию: z=????+????∗w.

Теперь нам требуется подобрать такие значения A и B, для которых функция будет минимальной:



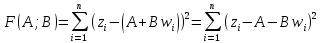
Найденная функция стремится к минимуму:



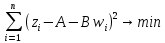
Продифференцируем ее по переменным А, В и приравняем к нулю:



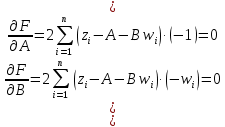
В результате умножения под знаком суммы получаем следующую систему уравнений:



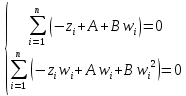
После раскрытия скобок получаем систему:



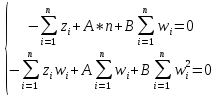
В результате всех преобразований получаем следующую систему двух линейных уравнений с двумя неизвестными:



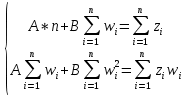
Составляем матрицу, используя предыдущую систему:



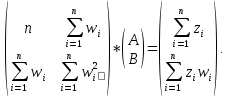
Далее, для того чтобы мы смогли рассчитать коэффициенты данной математической модели, нам необходимо знать дополнительные данные (таблица 2):

---

Смотрите также файлы

• маркетинг.docx

• Организация высшего образования.docx

• А блімі Блімаралы таырып бойынша жиынты баалау.docx

• Задача круг уравнение неизвестная тема урока Уравнения Тема урока.pptx

• Передача информации в компьютерных сетях Требования к знаниям и умениям учащихся.docx