Файл: Кодирование данных, комбинаторика, системы счисления.doc

Скачать файл
Заказать решение

ВУЗ: Не указан

Категория: Не указан

Дисциплина: Не указана

Добавлен: 12.01.2024

Просмотров: 380

Скачиваний: 2

ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.

*АА** *А*А* *А**А

они дают 3 · 27 = 81 комбинацию

  1. два шаблона, где первая по счёту буква А стоит на третьей позиции:

**АА* **А*А

они дают 2 · 27 = 54 комбинации

  1. и один шаблон, где сочетание АА стоит в конце

***АА

они дают 27 комбинаций

  1. всего получаем (4 + 3 + 2 + 1) · 27 = 270 комбинаций

  2. ответ: 270.

Решение (вариант 2, использование формул комбинаторики):

  1. в последовательности из 5 символов нужно использовать ровно две буквы А и три символа, не совпадающих с А, которые обозначим звездочкой

  2. сначала найдём количество перестановок из двух букв А и трёх звёздочек

  3. используем формулу для вычисления числа перестановок с повторениями; для двух разных символов она выглядит так:



Здесь – количество букв А, – количество звёздочек и восклицательный знак обозначает факториал натурального числа, то есть произведение всех натуральных чисел от 1 до :

  1. в нашем случае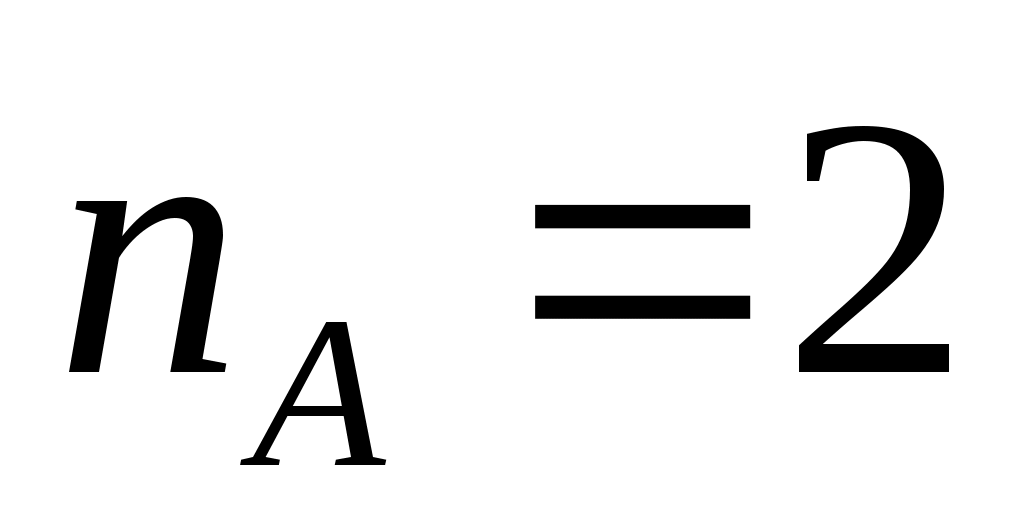 и 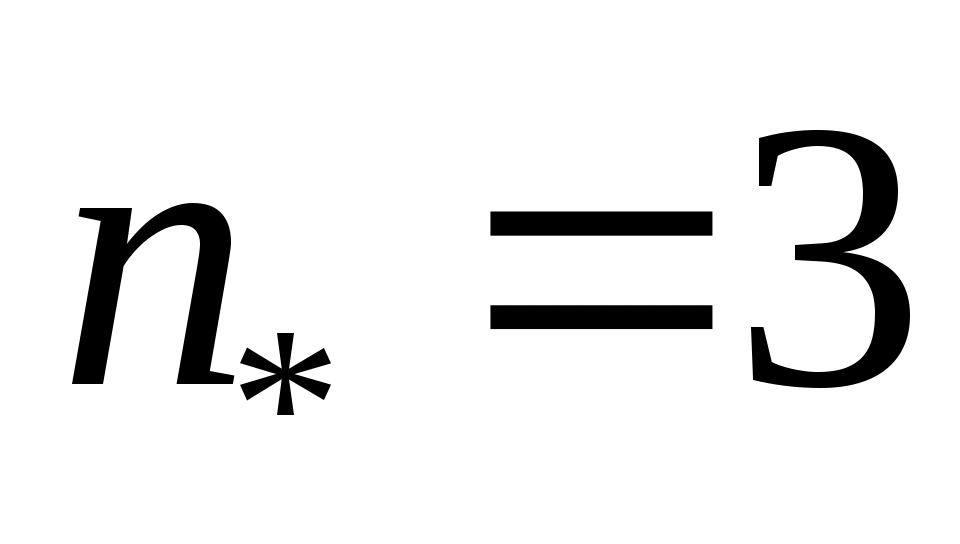, так что получаем



  1. теперь разберёмся со звёздочками: вместо каждой из них может стоять любой из трёх символов (кроме А), то есть на каждую из 10 перестановок мы имеем 33 = 27 вариантов распределения остальных символов на месте звёздочек

  2. таким образом, получаем всего 10 · 27 = 270 вариантов.

  3. ответ: 270.

Решение (с помощью программы, С.С. Поляков):

  1. для построения множества всевозможных слов можно использовать функцию product из модуля itertools; затем остаётся выбрать и пересчитать подходящие слова:

from itertools import product

p = product('ACGT',repeat=5)

s = map(lambda x: ''.join(x), p)

n = 0

for x in s:

if (x.count('A') == 2):

n += 1

print(n)

  1. Ответ: 270.

Решение (с помощью программы, Б.С. Михлин):

  1. можно использовать «метод грубой силы» – перебор всех вариантов:

n=0

s='acgt'

for a in s:

for b in s:

for c in s:

for d in s:

for e in s:

if (a+b+c+d+e).count('a')==2: # буква 'a' (латинская)

# должна встречаться два раза

n+=1

print(n)

  1. Ответ: 270.

Ещё пример задания:


Р-04. Сколько слов длины 5, начинающихся с гласной буквы, можно составить из букв Е, Г, Э? Каждая буква может входить в слово несколько раз. Слова не обязательно должны быть осмысленными словами русского языка.

Решение:

  1. первая буква слова может быть выбрана двумя способами (Е или Э), остальные – тремя

  2. общее число различных слов равно 2*3*3*3*3 = 162

  3. ответ: 162.

Решение (через формулы, А.Н. Носкин):

  1. Дано слово длиной 5 символов типа *****, где красная звездочка – гласная буква (Е или Э), а черная буква любая из трёх заданных.

  2. Общая формула количества вариантов:

N = ML, где М – мощность алфавита, а L – длина кода.

  1. Так как положение одной из букв строго регламентировано (знак умножения в зависимых событиях), то формула всех вариантов примет вид: N = M1L1 ∙ M2L2,

  2. Тогда M1 = 2 (алфавит гласных букв), а L1 = 1 (только 1 позиция в слове).

M2 = 3 (алфавит всех букв), а L2 = 4 (оставшиеся 4 позиции в слове).

  1. В итоге получаем: N = 21 ∙ 34 = 2 ∙ 81 = 162.

  2. ответ: 162.

Решение (с помощью программы, С.С. Поляков):

  1. для построения множества всевозможных слов можно использовать функцию product из модуля itertools; затем остаётся выбрать и пересчитать подходящие слова:

from itertools import product

p = product('ЕГЭ',repeat=5)

s = map(lambda x: ''.join(x), p)

n = 0

for x in s:

if (x[0] == 'Е') or (x[0] == 'Э'):

n += 1

print(n)

  1. Ответ: 162.

Решение (с помощью программы, Б.С. Михлин):

  1. можно использовать «метод грубой силы» – перебор всех вариантов:

n=0

s='егэ'

for a in 'еэ': # первая буква должна быть гласной

for b in s:

for c in s:

for d in s:

for e in s:

n+=1

print(n)

  1. Ответ: 162.

Ещё пример задания:


Р-03. Все 4-буквенные слова, составленные из букв К, Л, Р, Т, записаны в алфавитном порядке и пронумерованы. Вот начало списка:


1. КККК

2. КККЛ

3. КККР

4. КККТ

……

Запишите слово, которое стоит на 67-м месте от начала списка.

Решение:

  1. самый простой вариант решения этой задачи – использование систем счисления; действительно, здесь расстановка слов в алфавитном порядке равносильна расстановке по возрастанию чисел, записанных в четверичной системе счисления (основание системы счисления равно количеству используемых букв)

  2. выполним замену К0, Л1, Р2, Т3; поскольку нумерация слов начинается с единицы, а первое число КККК0000 равно 0, под номером 67 будет стоять число 66, которое нужно перевести в четверичную систему: 66 = 10024

  3. Выполнив обратную замену (цифр на буквы), получаем слово ЛККР.

  4. Ответ: ЛККР.

Решение (с помощью программы, А.Н. Носкин):

  1. на компьютерном ЕГЭ можно использовать программу (язык Python):

a = ["К", "Л", "Р", "Т"] # буквы К, Л, Р, Т записаны в алфавитном

# порядке

s = ""    # строка для формирования ответа

x = 66 # числовой код слова: 67-1 = 66

while x > 0: # перевод в 4-ю систему счисления

    s += str(x%4)

    x //= 4

s =  s[::-1] # реверс строки ответа

for x in s: # формирование СЛОВА

    i = int(x)

    print( a[i], end="" )

  1. Ответ: ЛККР.

Решение (с помощью программы, С.С. Поляков):

  1. программа на языке Python использует модуль itertools:

from itertools import product

print(*list(product('КЛРТ',repeat=4))[67-1])

  1. Ответ: ЛККР.

Решение (с помощью программы, Б.С. Михлин):

  1. можно использовать «метод грубой силы» – перебор всех вариантов:

n=0

s='клрт'

for a in s:

for b in s:

for c in s:

for d in s:

n+=1

if n==67:

print(a+b+c+d)

exit() # выход из Python

  1. другой вариант (с «флажком» для входа из вложенного цикла) :

n=0

s='клрт'

fl=False # флажок сброшен

for a in s:

if fl: break


for b in s:

if fl: break

for c in s:

if fl: break

for d in s:

n+=1

if n==67:

print(a+b+c+d)

fl=True # флажок установлен для выхода

break

  1. Ответ: ЛККР.

Смотрите также файлы