Федеральное агентство связи ОрденаТрудового Красного Знаменифедеральное бюджетное образовательное учреждение высшего образования«Московский Технический Университет Связи и Информатики»(МТУСИ)Кафедра ИнформатикиПредмет: Численные методыЛабораторная работа № 2Вариант 22Выполнил: Иван ИвановВыбор и нумерация узлов для формулы Ньютона Для ручной интерполяции в точке x=a=0.17  по 1-й формуле Ньютона выбираем 4 узла из таблицы 2-2 так, чтобы точка a=0.17  оказалась между узлами с номерами с 1 по 2 и добавляем узлы вправо:

№	xk	yk
2	0.15	-4.0845
3	0.20	-4.0240
4	0.25	-3.9500
5	0.30	-3.8610

k	0	1	2	3
xk	0.15	0.20	0.25	0.30
yk	-4.0845	-4.0240	-3.9500	-3.8610

x	y	Δy	Δ2y	Δ3y
0.15	-4.0845	0.0605	0.0135	0.0025
0.20	-4.0240	0.0740	0.016
0.25	-3.9500	0.09
0.30	-3.8610

---

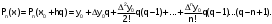
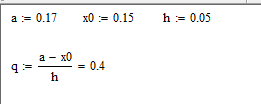
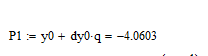
Запишем 1–ю интерполяционную формулу Ньютона для многочленов 1–й, 2–й и 3–й степени и выполним расчеты по ним. Определим значение q:Значение многочлена 1-й степени в т. x=0.17:Значение многочлена 2-й степени в т. x=0.17:Значение многочлена 3-й степени в т. x=0.17:

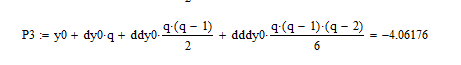
Степень многочлена k	Pk(x)	Погрешность
1	-4.06030	0.00162
2	-4.06192	0.00016
3	–4.06176	–

Погрешность = Pk+1-PkВывод.Получены выражения для интерполяционных многочленов 1, 2 и 3-ей степени и их значения в т. а. Оценку погрешности проведём в соответствии с неравенством:Можно утверждать, что разность между точным значением функции и значением функции в т.x=0.17 после 3-х итераций не превышает 0.00016.

---

Смотрите также файлы

• Решение Избыточное давление жидкости в полости цилиндра (1) где плотность жидкости.docx

• После стирки мылом и полоскания на темной одежде образовался седой налет.docx

• знать определение поворота и уметь доказывать, что он является движением.docx

• Контрольная работа по теме Доказательства по дисциплине Спецмодуль Философия. Логика.docx

• Место придаточного предложения по отношению к главному. Знаки препинания в спп. Цели урока.docx