ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 12.01.2024
Просмотров: 21
Скачиваний: 2
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
3) Шекаралық қабаттың негізгі теңдеулері
Шекаралық қабат теориясындағы әртүрлі теңдеулерді талдау кезінде шешімдердің сол немесе басқа функциялар класына жататынын анықтау мәселесі туындайды. Сол теңдеулерінің шешімдерінің дифференциалдық қасиеттерін алдын ала білу қажет. Осыған байланысты шекаралық қабаттың теңдеулерін олардың математикалық қасиеттерін айқынырақ көрсететін түрге түрлендіру мүмкіндігі ерекше рөл атқарады. Ньютондық тұтқыр сұйықтықтарда динамикалық шекаралық қабат ішкі үйкеліс күштері басым рөл атқаратын ағын аймағы ретінде түсінілетіні белгілі болды. Ньютон заңы бойынша тұтқыр күштердің қарқындылығы ығысу жылдамдығымен сызықты түрде Рейнольдс сандарында байланысты.
Үйкеліс кернеуі қабырғадағы максималды мәннен сыртқы шекарада жоғалып бара жатқан шамаға тән өлшеммен салыстырғанда анықталатын жұқа аймақты, тұтқыр шекара қабаты деп атайды. Ньютондық сұйықтардың шекаралық қабаттарын зерттей келе мынандай болжам жасай аламыз: Ньютондық сұйықтардан тек тұтқыр күштердің интенсивтілігі ығысу жылдамдығына тәуелділігімен ерекшеленетін аномальды-тұтқыр сұйықтықтардың ағынында инерциямен салыстырғанда ішкі үйкеліс күштерінің басым әсер ету облысы, яғни тұтқыр шекаралық қабат болуы мүмкін. Дегенмен, шекаралық қабаттың идеяларын аномальды тұтқыр сұйықтықтарға дейін кеңейтуге сақтықпен қарау керек. Үйкеліс кернеуі ығысу жылдамдығына әлсіз тәуелді болатын аномальды-тұтқыр сұйықтықты елестетейік. Бұл жағдайда тұтқыр күштердің басым әсерінің жеткілікті айқын аумағы болмайды, ал шекаралық қабаттың гипотезасы өзінің жарамдылығын жоғалтады.
Навье-Стокс теңдеулері тұтқыр сұйықтықтың Ньютон моделіне негізделген. Бұл модельге сәйкес, сұйықтықтағы ығысу кернеулері сәйкес ығысу деформация жылдамдығына сызықтық тәуелді. Атап айтқанда, екінші ретті дербес туындылары кіретін Навье-Стокс теңдеулер жүйесінің негізгі бөлігінің формасын анықтауға мүмкіндік береді. Тұтқыр сұйықтықтың бұл моделі әрқашан дұрыс емес. Полимерлердің балқымалары мен ерітінділері, концентрлі суспензиялар, эмульсиялар, бояғыштар Ньютон моделіне сәйкес келмейтін орталардың мысалдары болып табылады.
Ньютондық емес сұйықтықтардың динамикасын сипаттау үшін көптеген әртүрлі модельдер ұсынылды (мысалы, Литвинов, Шульман). Сызықтық емес тұтқыр сұйықтықтардың бір моделі-Оствальд моделі, онда кернеу тензорының компоненттері деформацияның дәрежелік жылдамдық тензор компоненттеріне тәуелді. Бұл модельді толығырақ сипаттайық.
Егер u1, u2, u3 – x1, x2, x3 координаталар жүйесіндегі сұйықтық жылдамдығының құраушылары болса, ал
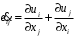(3.1)деформация жылдамдығы тензорының құрамдас бөліктері болып табылады.
Онда кернеу тензоры (τij) үшін Ньютондық емес сұйықтықтың қуат заңы моделінде келесі тәуелділік қабылданады:
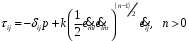(3.2)мұндағы, p – қысым, k – сұйық консистенция индексі, δij – Кронеккер таңбасы.
Күш заңы сұйықтықтары аномальды тұтқыр сұйықтықтардың әрекетінің тәжірибесі үшін ең қарапайым және сонымен бірге қанағаттанарлық сандық сипаттаманы қамтамасыз етеді. 0 < n < 1 үшін сұйықтық псевдопластикалық, ал n > 1 дилатантты сұйықтық, сәйкесінше n = 1 үшін қарапайым Ньютондық сұйықтық.
Күш заңы бойынша сығылмайтын сұйықтың қозғалысы келесі теңдеулер жүйесімен сипатталады, ол Навье-Стокс теңдеулер жүйесінің табиғи қорытылуы болып табылады:
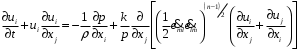
(3.3)
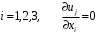
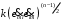мәні сұйықтықтың тиімді тұтқырлығы деп аталады және n ≠ 1 кезінде ығысу деформация жылдамдығының шамасына байланысты.Кәдімгі қасиеттері бар сұйықтықтардағы сияқты, бұл беттердің жанында қатты беттердің айналасында аномальді тұтқыр сұйықтық ағып жатқанда, инерциялық күштермен салыстырғанда ішкі үйкеліс күштерінің басым әсер ету аймағы, яғни тұтқыр шекаралық қабат болуы мүмкін деп болжай аламыз. Прандтль гипотезасын дұрыс деп есептей отырып, (3.1)-ден шекаралық қабаттағы сұйықтықтың қозғалысын сипаттайтын және Прандтль теңдеулер жүйесінің жалпылама нұсқасы болып табылатын теңдеулер жүйесін шығаруға болады:
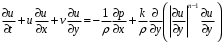
(3.4)
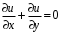
Жүйенің (3.4) туындысының толығырақ берілуі, сондай-ақ осы жүйемен байланысты әртүрлі өзіндік ұқсас есептердің шешімі, Шульман мен Берковскийдің кітабында қамтылған, және оны толығымен келесі тақырыпшаларда қарастырылады.
Шульман мен Берковскийдің қорытулары бойынша:
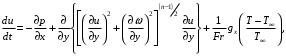
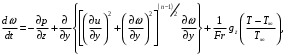(3.5)
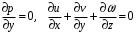
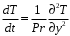(3.6)Үлкен Рейнольдс сандарындағы өлшемсіз көлденең координатаның соңғы мәндері өлшемдік координатаның кіші мәндеріне сәйкес келеді. Демек, (3.5), (3.6) алынған теңдеулер сұйықтың нөлдік ағын сызығына жақын жіңішке аймақтағы қозғалысын сипаттайды. Бұл аймақты шекаралық қабат деп атаймыз, ал (3.5), (3.6) теңдеулерін – дәрежелік реологиялық заңға бағынатын сұйықтықтардың шекаралық қабатының теңдеулері.
Ауырлық күштері инерция күштерінен әлдеқайда аз және, демек,
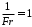болғанда, қалыпты температура айырмашылығы кезінде мәжбүрлі конвекция есептері үшін (3.5) теңдеулердің соңғы мүшелерін елемеуге болады.Қозғалмайтын жазық-параллель симметриялық ағынның шекаралық қабатындағы псевдопластикалық сұйықтықтың қозғалысы мына түрдегі теңдеулер жүйесімен сипатталады:
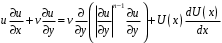
(3.7)
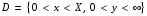аймағында, келесі шарттар қолданылады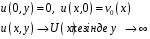
Сонымен бірге,
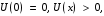кезінде 
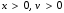және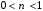 
деп қабылданады.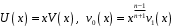
деп болжау жасасақ,
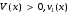– шектеулі функциялар. Өзгеріске ұшырамайтын жаңа айнымалыларға көшейік: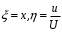
және жаңа белгісіз функцияны енгізейік:
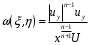
Сонда (3.7) теңдеу мынандай түрге айналады:
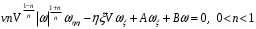
мұндағы A, B – тұрақтылар, және олар келесі тепе-теңдікті қамтиды,
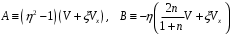
Симметриялық шекаралық қабаттағы псевдопластикалық сұйықтықтың тұрақсыз қозғалысы келесі түрдегі теңдеулер жүйесімен сипатталады:
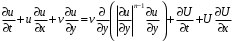
(3.8)
Тұрақсыз қозғалыста
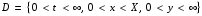
аймағы орын алып, келесі шарттар қолданылады:
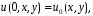
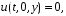
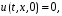
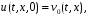
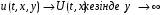
Мынандай болжау жасаймыз,
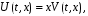
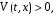
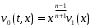
мұндағы
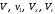– шектеулі функциялар. Псевдопластикалық тұрақты қозғалыстағыдай жаңа айнымалылар мен функцияға көшетін болсақ: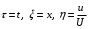
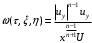
Нәтижесінде жоғарыдағы жүйе мына түрге келеді:
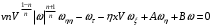
Қазіргі уақытта бастапқы жылдамдық профиліне қойылатын қосымша шарттарсыз қабаттың жалғасу мәселесінің жалпы жағдайында дилатант орта үшін шекаралық қабат теңдеулер жүйесін шешудің бірегейлігі туралы мәселе ашық күйінде қалып отыр. Дилатант сұйықтарының шекаралық қабаты үшін стационарлы емес теңдеулер жүйесінің шешілетіндігі туралы қатаң математикалық нәтижелер жоқ.
Қорыта айтатын болсақ, реологиялық сұйықтардың шекаралық теңдеулерін зерттеу үшін, қалыпты жағдайдағы, яғни Ньютондық сұйықтардың шекаралық теңдеулеріне жүгінеміз. Алайда, осы Ньютондық емес сұйықтардың теңдеулерін шешу оңайға түспейді, сондықтан оны математикалық анализден өткізу жөн. Соның арқасында, Ньютондық емес сұйықтардың интенсивтілігі ығысу жылдамдығына тәуелді екекніне көзіміз жетті.
Пайдаланылған әдебиеттер тізімі
1) Шлихтинг Г. Теория пограничного слоя / Г. Шлихтинг. М.: Наука. 2004. 714 с.
2) Олейник О.А., Самохин В.Н. Математические методы в теории пограничного слоя. М.: Наука. 1997. 508 с.
3) Берковский Б.М. Пограничный слой неньютоновских жидкостей. Минск: Наука и техника. 2009. 239 с.