Файл: Реферат по дисциплине Численные методы расчета строительных конструкций по теме Переход от реального объекта к расчётной схеме.docx

Министерство образования и науки Российской федерацииФедеральное государственное автономное образовательное учреждение высшего образования«Южно-Уральский государственный университет (НИУ)»Архитектурно-строительный институтКафедра "Строительные конструкции и сооружения"Рефератпо дисциплине «Численные методы расчета строительных конструкций»по теме: «Переход от реального объекта к расчётной схеме»Оглавление

1. 
   Расчетная схема……………………..…………………………………………..3
   
2. 
   Численные методы………………..………………………………………….…5
   
3. 
   Библиографический список……………………………………………………11
   

Расчетная схемаВ фундаментальных науках исследуются свойства и характеристики идеализированных конструкций, сделанных из сплошных изотропных материалов, работающих в нейтральной окружающей среде. Из реальной конструкции выкристаллизовываются её атрибутивные признаки, совокупность которых представляет собой расчётную схему (идеализированную конструкцию). Первым шагом в данном направлении является упрощение (Формализация) исследуемой реальной модели конструкции, т.е. освобождение от несущественных в данной задаче особенностей, которые не могут заметным образом повлиять на работу системы в целом. Степень упрощения зависит от требуемой точности, математических возможностей, а также от того, какая сторона явления рассматривается в задаче. Полученная в итоге модель есть расчетная схема объекта, отражающая наиболее существенные особенности реального объекта, определяющие его поведение под нагрузкой (рис.1)Однако при выборе расчетной схемы следует придерживаться следующих правил:1)Аппроксимирующая модель работы проектируемого объекта должна правильно и полно отражать работу реального объекта, т.е. соответствовать механизмам его деформирования и разрушения.2)Принимаемая расчетная гипотеза должна ставить рассчитываемую конструкцию в менее благоприятные условия, чем те в которых находится действительная конструкция.3)Расчетная модель работы сооружения должна быть достаточно простой. Целесообразно иметь не одну модель, а

---

систему аппроксимирующих моделей, каждая из которых имеет свои границы применения.



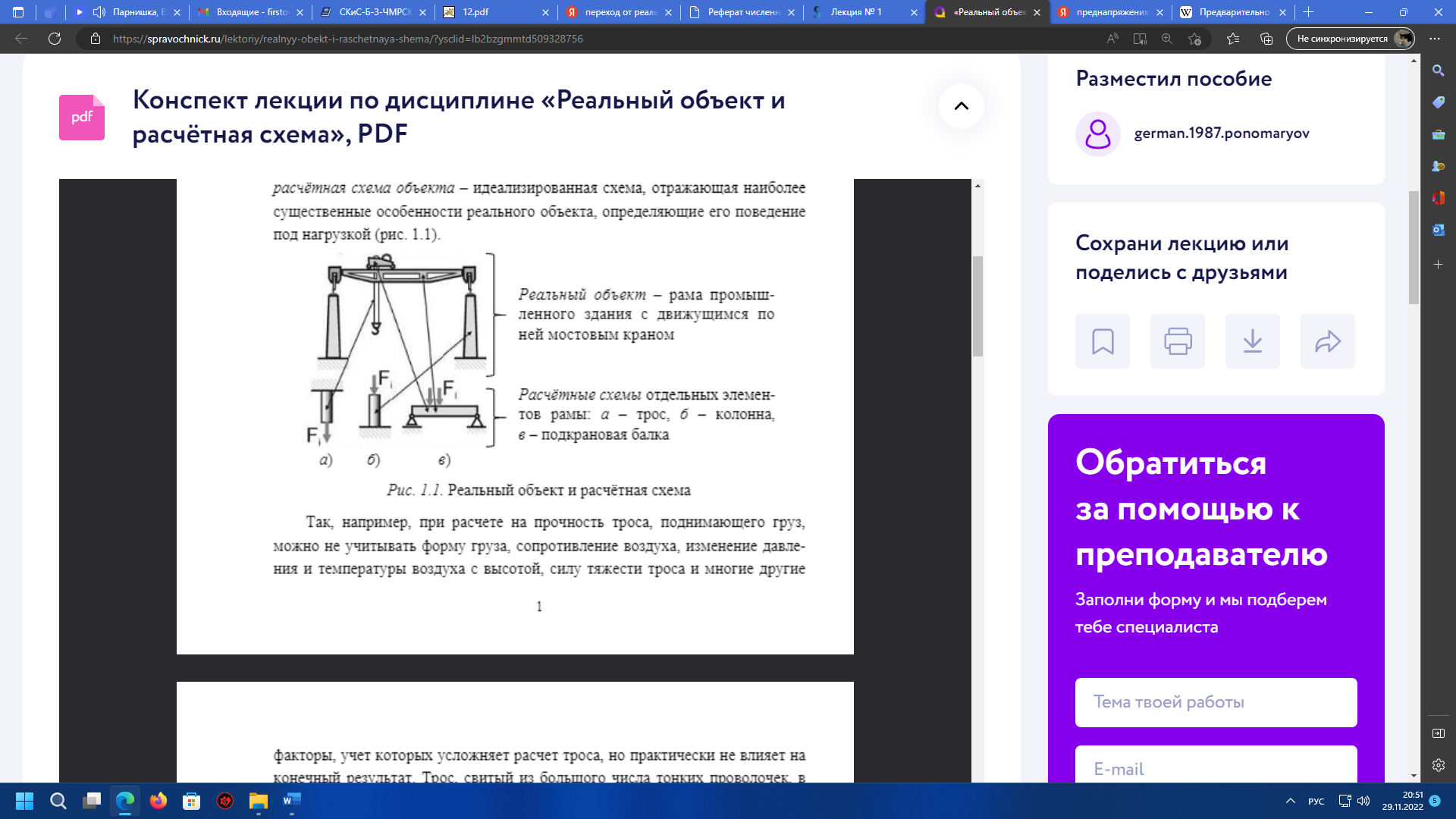
Рисунок 1. Реальный объект и расчетная схема

В качестве примера на рис.2 приведена консольная балка, как при испытаниях изобразил ее Галилео Галилей (а), и ее расчетная схема (б).



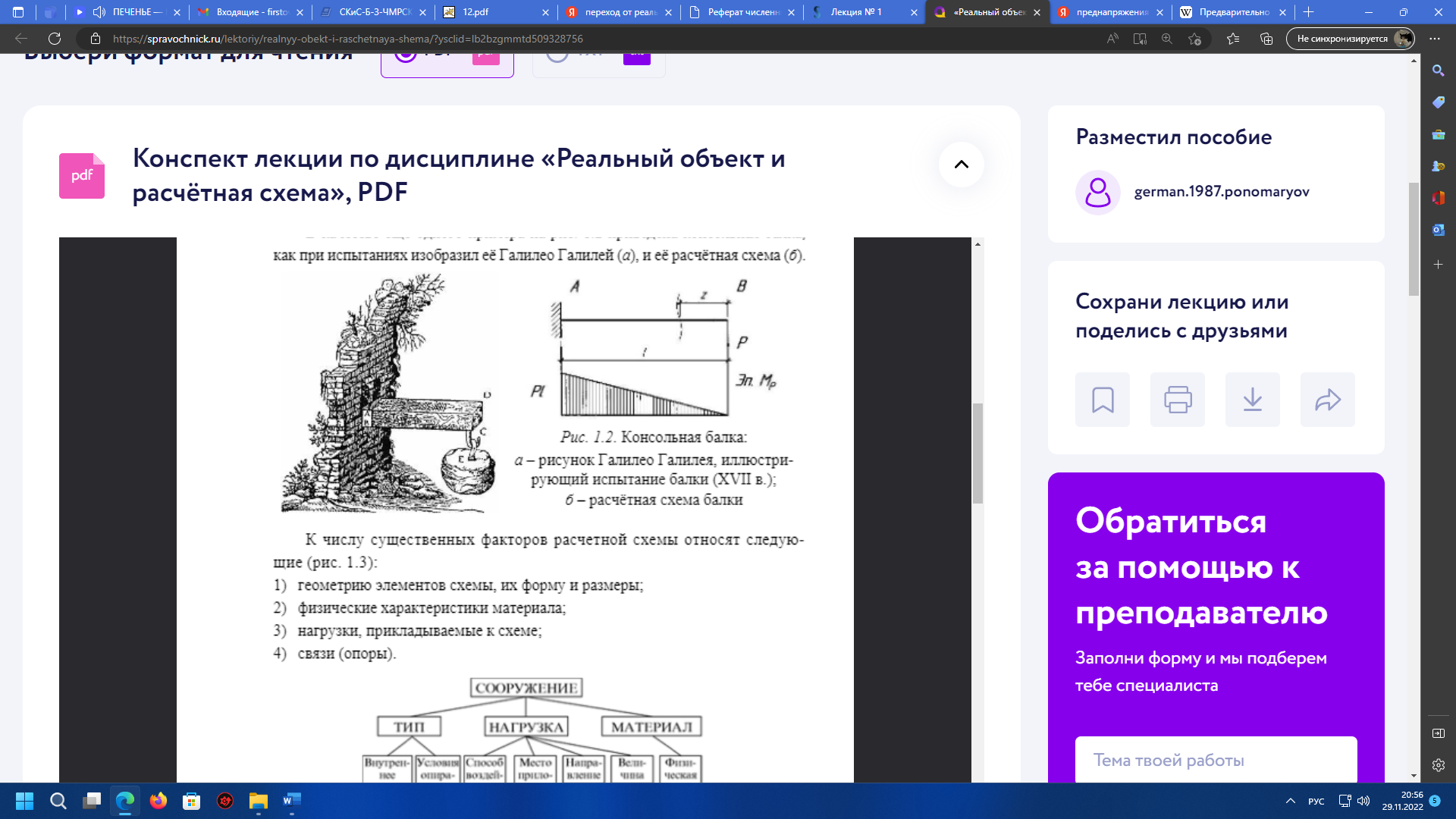
Рисунок 2. Консольная балка: а – рисунок Галилео Галилея, иллюстрирующий испытание балки (ХVII в.) б – расчетная схема балки

К числу существенных факторов расчетной схемы относят следующие:

1. 
   Геометрию элементов схемы, их форму и размеры;
   
2. 
   Физические характеристики материала;
   
3. 
   Нагрузки, прикладываемые к схеме;
   
4. 
   Связи (опоры).
   

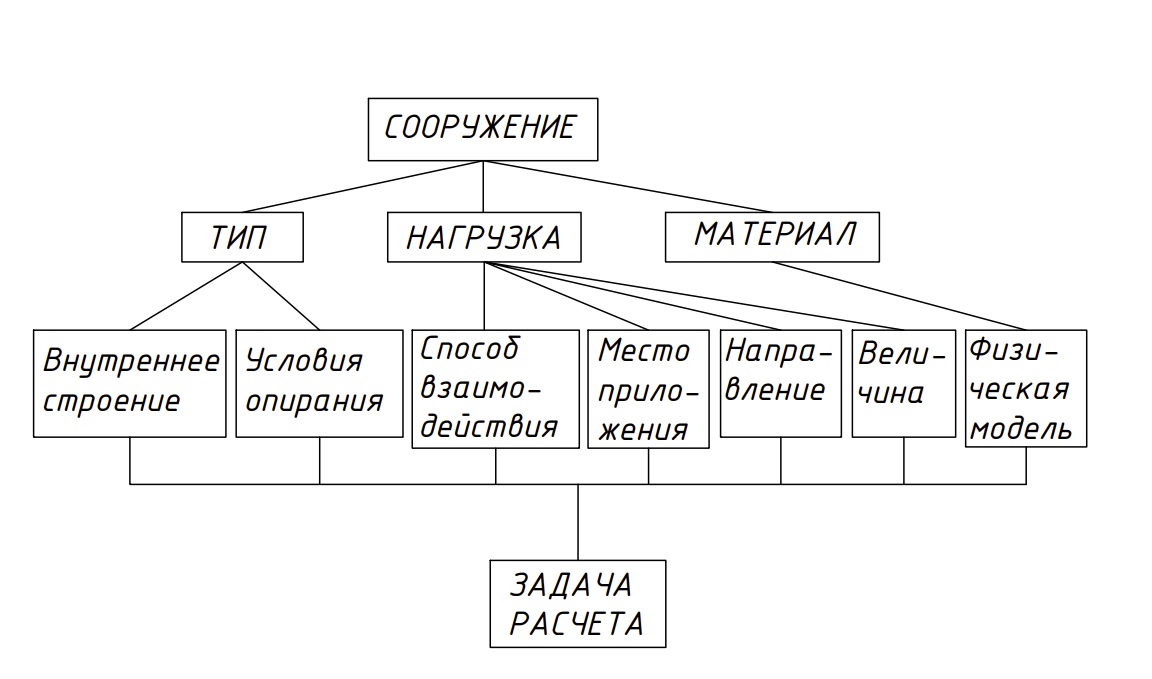
Рисунок 3. Существенные факторы расчетной схемы сооруженияЧисленные методыСовременный уровень развития компьютерных технологий определил специфику методов расчета строительных конструкций на прочность, жесткость и устойчивость. Если несколько десятилетий назад преобладали аналитические методы определения НДС элементов сооружений, а также экспериментальные исследования, то сейчас при бурном развитии электронно-вычислительных машин (ЭВМ) в строительной механике начинают превалировать численные методы расчета строительных конструкций.Численные методы по определению являются приближенными. Вместо того чтобы разыскивать сложные функции, удовлетворяющие дифференциальным уравнениям, описывающим исследуемое явление, и краевым условиям, вводят набор известных простых (очень часто – кусочно-непрерывных) базисных функций, с помощью которых находят производные, входящие в дифференциальные уравнения или выражения механической энергии изучаемого объекта. В итоге непрерывная функция одного или нескольких аргументов представляется ее значениями в некоторых точках (узлах), а операции анализа непрерывных функций заменяются алгебраическими действиями со значениями функций в выбранной сетке узлов. Таким образом, численные методы приводят решение физико-математических задач к простейшим вычислительным процедурам, которые выполняются, как правило, с помощью ЭВМ.

---

Метод конечных разностей

Метод конечных разностей (МКР) является приближенным методом решения краевых задач для дифференциальных уравнений. Его еще называют методом сеток. Существо метода следующее. На рассматриваемую область (ось стержня, срединную поверхность оболочки или объемное тело) наносим сетку узлов (соответственно одномерную, двумерную или трехмерную). Производные, которые входят в дифференциальные уравнения, описывающие деформирование элементов строительных конструкций, и краевые условия приближенно заменяем соответствующими разностными соотношениями по формулам численного дифференцирования и, следовательно, выражаем через неизвестные значения искомой функции в узлах сетки. В результате сводим задачу к системе алгебраических уравнений, в которой неизвестными величинами являются значения искомых функций в узлах ранее созданной сетки. Решив эту систему и, при необходимости, проинтерполировав узловые значения искомых функций в промежутках между узлами сетки, в итоге получим приближенное численное решение поставленной задачи.Существенное преимущество метода конечных разностей по отношению к другим численным методам – это несильная зависимость используемого алгоритма от вида дифференциальных уравнений и краевых условий задачи. Недостаток же состоит в том, что приходится решать системы алгебраических уравнений высоких порядков. Этот недостаток смягчается тем, что матрицы систем уравнений – неполностью заполненные (ленточные). Метод конечных разностей также затруднительно использовать при решении задач о сопряжении конструкций различной размерности (например, оболочек и объемных тел), многосвязных (с вырезами), при смешанных граничных условиях и т.д.

Вариационно-разностный метод

Вариационно-разностный метод (ВРМ) базируется на вариационных принципах механики и свободен от ряда недостатков, присущих МКР. В данном случае деформирование строительной конструкции описывается неким функционалом, чаще всего это выражение потенциальной энергии системы – функционал Лагранжа, который в положении равновесия системы является стационарным. Условие стационарности функционала соответствует дифференциальным уравнениям, которыми описывается поведение изучаемой системы, однако порядок производных, входящих в функционал, ниже порядка производных в дифференциальных уравнениях, что дает возможность упростить алгоритмизацию процесса решения задачи. Кроме того, ВРМ позволяет упростить запись граничных условий. Так, при использовании функционала Лагранжа требуется удовлетворять только кинематическим краевым условиям, так как статические условия уже содержатся в вариационных уравнениях. Эти условия называют естественными.

---

При реализации ВРМ вариационная задача заменяется конечно- разностным аналогом па заранее выбранной сетке узлов, т.е. производные от непрерывных функций, входящих в выражение, например, потенциальной энергии рассматриваемой системы, определяются численно в назначенных узлах с помощью конечно-разностных соотношений. Кроме того, ввиду необходимости вычисления определенного интеграла, входящего в выражение функционала энергии, в областях рассматриваемой системы между узлами вводят кусочно-непрерывные так называемые функции восполнения. От характера этих функций зависит степень конечно-разностной аппроксимации. В итоге процедура ВРМ сводится к хорошо обусловленной симметричной системе алгебраических уравнений (при использовании функционала Лагранжа) ленточной структуры.

Метод конечных элементов

В последнее время для расчета строительных конструкций с помощью ЭВМ широкое распространение получил метод конечных элементов (МКЭ). Суть этого метода заложена в его названии: рассчитываемую систему (стержневую или континуальную) разбивают на определенное число отдельных частей конечных размеров (конечных элементов), имеющих те же физико-механические характеристики, что и заданная конструкция. После этого точно или приближенно изучают напряженно-деформированное состояние каждого конечного элемента методами, известными в строительной механике и теории упругости: сил, перемещений или смешанным, с целью определения в зависимости от принятого метода анализа усилий, или перемещений, или и того и другого в точках соединения конечных элементов между собой (узлах). Эти факторы принимают в качестве основных неизвестных метода конечных элементов. Для нахождения неизвестных составляют и решают систему алгебраических уравнений, как правило, очень высокого порядка (десятки, сотни тысяч и миллионы уравнений).В практических расчетах строительных конструкций и объектов машиностроения наиболее распространен вариант МКЭ, основанный па идее метода перемещений, поэтому ограничимся рассмотрением этой формы метода. Метод конечных элементов в перемещениях оказался очень приспособленным к использованию ЭВМ, так как при анализе отдельных конечных элементов приходится иметь дело с простыми геометрически подобными объектами, стандартно закрепленными по контуру. Матрица системы алгебраических уравнений в данном случае является симметричной, ленточной и положительно определенной. Такую систему относительно легко решать. Применение же, например, варианта МКЭ в форме смешанного метода или метода сил не всегда приводит к системам уравнений с симметричными положительно определенными матрицами. Их решение производится, как правило, с помощью специальных более сложных алгоритмов.

---

При реализации метода конечных элементов в перемещениях в качестве основных неизвестных принимают обязательно поступательные перемещения, а в некоторых конечноэлементных моделях – дополнительно и углы поворота в узлах.Подход к прочностным расчетам, основанный на МКЭ в перемещениях, является единым как для дискретных (стержневых) систем, так и для континуальных: пластин, оболочек, массивных тел. Разница состоит лишь в применяемых основных типах конечных элементов: стержневых, плоских треугольных и четырехугольных, аналогичных оболочечных, криволинейных оболочечных и объемных.Стержневые элементы могут быть с шарнирами по концам, работающие только на растяжение и сжатие, изгибаемые плоские и пространственные и общего вида, испытывающие все виды деформаций: растяжение, сжатие, изгиб и сдвиг в двух плоскостях и кручение.Плоские элементы могут деформироваться в своей плоскости (плоская задача теории упругости) или из плоскости (задача изгиба пластины). Плоские оболочечные элементы сочетают оба вида деформации: в своей плоскости и из плоскости, но не учитывают взаимного влияния этих видов деформаций. Криволинейные оболочечные элементы учитывают взаимодействие двух видов деформаций, точнее описывают заданную геометрию изучаемой системы, но в реализации оказываются более громоздкими.Объемные конечноэлементные модели имеют формы пирамид, призм, параллелепипедов или аналогичных криволинейных тел. Их обычно применяют в расчетах массивных объектов: плотин, мостовых опор, массивов грунта и т.д., т.е. там, где требуется решение объемной задачи теории упругости.

Метод граничных элементов

Метод конечных элементов весьма привлекателен для инженеров-расчетчиков в связи с тем, что возможная достаточно сложная геометрия объекта исследования (стержневая или тонкостенная пространственная система, объемное тело и т.д.) достаточно точно аппроксимируется конечноэлементной моделью. Сравнительно легко учитываются условия закрепления конструкции и ее нелинейные свойства (геометрическая, физическая и конструктивная нелинейности). Однако реализация МКЭ связана с необходимостью разбиения на конечные элементы (дискретнзации) всего рассматриваемого объекта, что в свою очередь приводит к необходимости решения систем алгебраических уравнений высоких порядков. Кроме того, метод не всегда обеспечивает непрерывность перемещений или их производных, т.е. совместность деформаций на границах контакта конечных элементов. 

---