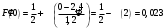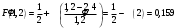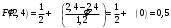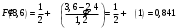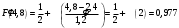№3.

Дискретная случайная величина X (ДСВ X) задана законом распределения p(x) с параметром α при целом неотрицательном x. Требуется:

а) составить ряд распределения случайной величины X (СВ X);

б) построить многоугольник распределения;

в) найти M(X), D(X), σ(X);

г) найти функцию распределения и построить ее график;

д) найти вероятность того, что СВ X попадет в интервал (0,5; 2,5);

е) найти вероятность того, что СВ X примет значение меньшее 1,5.
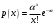, =0,3.
Решение:

а) данная случайная величина распределена по закону Пуассона. Очевидно, что x может принимать любые неотрицательные значения. Составим ряд распределения:

x=0:

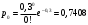
x=1:

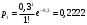
x=2:

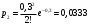
x=3:

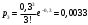
x=4:

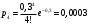
x=5:

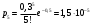
Запишем ряд распределения

x	0	1	2	3	4	5	6	…
p	0,7408	0,2222	0,0333	0,0033	0,0003	1,510-5	0	0

б) Изобразим ряд распределения графически в виде многоугольника распределения


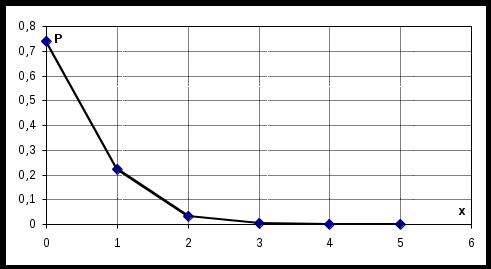
в) определим показатели распределения:

1) математическое ожидание:

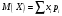=00,7408+10,2222+20,0333+30,0033+40,0003+51,510^-5+60+…=0,3.

2) для расчета дисперсии воспользуемся формулой:



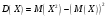
Найдем

---

:

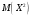
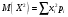=0²0,7408+1²0,2222+2²0,0333+3²0,0033+4²0,0003+5²1,510^-5+6²0+…=0,39.

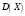=0,39-0,3²=0,3

3) среднее квадратическое отклонение равно: .
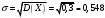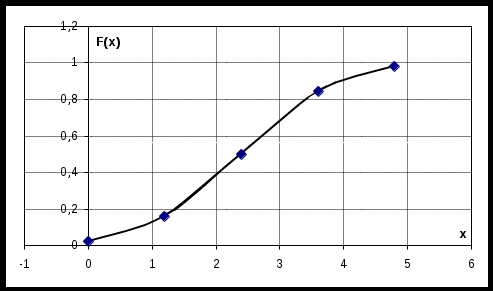
г) Составим функцию распределения:



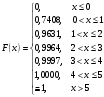
Построим график функции распределения


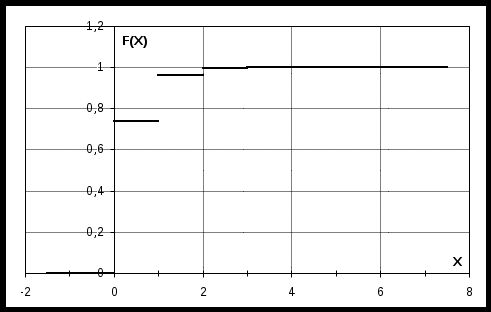
д) Р(0,5
е) Р(X<1,5)=F(1,5)=0,9631

№4.

Дифференциальная функция распределения СВ X имеет вид f(x)=Ag(x) при x₁≤x≤x₂ и f(x)=0 вне этого интервала. Требуется:

а) найти коэффициент A;

б) найти M(X), D(X), σ(X);

в) найти функцию распределения F(x);

г) построить графики F(x) и f(x), рассматривая не менее 5 точек на интервале [x₁;x₂];

д) найти вероятность попадания СВ X в интервал .
; .
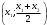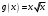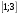Решение:

а) Для определения коэффициента А воспользуемся свойством плотности распределения:





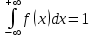
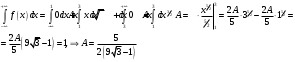
Плотность распределения будет равна

---

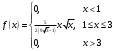
б) найдем M(X), D(X), σ(X)





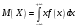
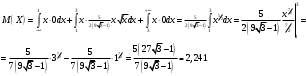
D(X)=M(X²)-(M(X))²






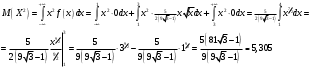
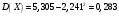
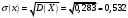
в) Найдем функцию распределения

1) если x1, то F(x)=0, т.к. значений, меньших 1, случайная величина не принимает.

2) если 1<x3, то



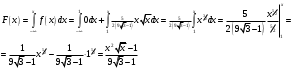
3) если x>3, то

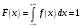в силу свойства плотности распределения

Окончательно получим:



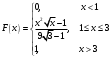
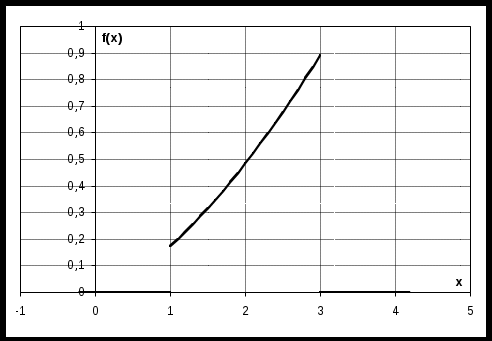
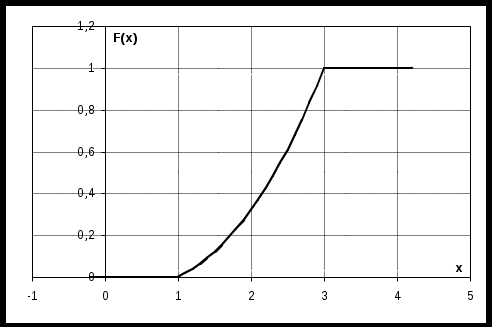
г) построим графики f(x) и F(x):







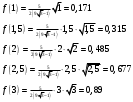
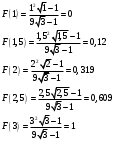
д)



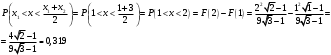
№5.

Найти вероятность попадания в интервал (-0,5;2) нормально распределенной СВ X, у которой задано математическое ожидание a и среднее квадратическое отклонение σ=0,5a. Записать функции F(x) и f(x) этого нормального закона и построить их графики на указанном интервале.
a=2,4 =0,5a=0,52,4=1,2
Решение:

Вероятность того, что случайная величина, распределенная по нормальному закону, попадет в интервал (;), определяется по формуле:

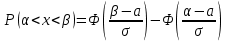, где a и  - математическое ожидание и среднее квадратическое отклонение случайной величины, а Ф(Х) – интегральная функция Лапласа.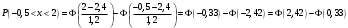



По таблице значений интегральной функции Лапласа находим: Ф(2,42)=0,4922, Ф(0,33)=0,1293. Тогда



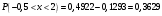
Плотность распределения для нормального закона задается формулой:

---

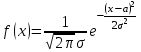, где a и  - математическое ожидание и среднее квадратическое отклонение.

Подставим а=2,4 и =1,2 в формулу:



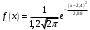
Построим ее график:












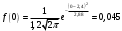
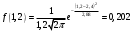
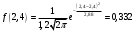
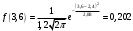
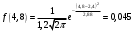
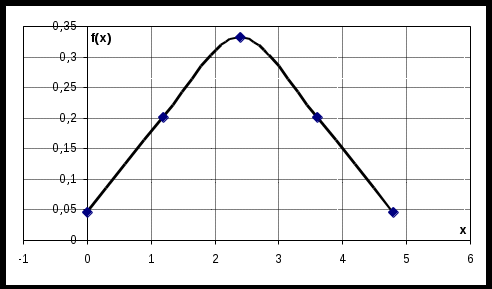
Функция распределения для нормального закона имеет вид:

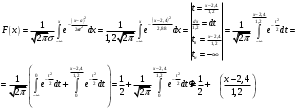
Построим ее график:

---

Смотрите также файлы

• Геофизический и гидродинамический контроль эксплуатации неоднородных коллекторов на основе инвариантных параметров в скважинах с высокотехнологичным заканчиванием.pdf

• Методические рекомендации по выполнению контрольной работы Приложение 6 к рабочей программе.doc

• Учебный план для 59 классов мкоу Левашинская гимназия.docx

• Программа среднего профессионального образования 44. 02. 03 Педагогика дополнительного образования (в области экологобиологической деятельности) Дисциплина Психология Практическое занятие 3.doc

• Решение Из выражения получим p , где r универсальнаягазовая постоянная m молярная масса воздуха.docx