ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 12.01.2024
Просмотров: 21
Скачиваний: 1
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
-
Цель работы
Разработать алгоритм и программу, реализующую спектральное разделение тестовой фонограммы на две области: НЧ (Fот и гармоники Fот) и ВЧ (формантную).
-
Описание этапов выполнения работы
Для выполнения лабораторной работы используем фонограмму под названием Music.aac. Частота дискретизации исходного звукового сигнала
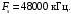Исходный звуковой сигнал во временной области представлен на рисунке 2.1.Частота основного тона
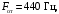таким образом частота среза для ФНЧ будет равняться 440 Гц. А так как форманта – максимум энергии в спектре звука, то, в соответствии со спектром исходного звукового сигнала, представленного на рисунке 2.2, частота среза для ФВЧ будет равняться 740 Гц.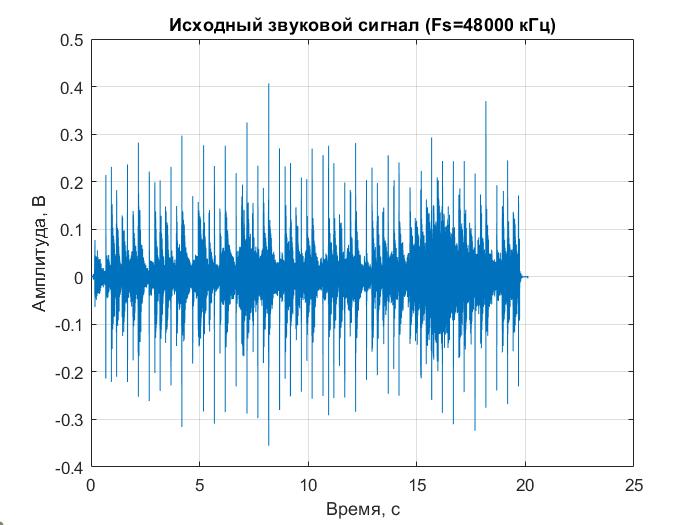 
Рисунок 2.1 – Исходный звуковой сигнал во временной области
С помощью алгоритма, описанного в функции FFT разложим спектр исходного звукового сигнала. Спектр представлен на рисунке 2.2.
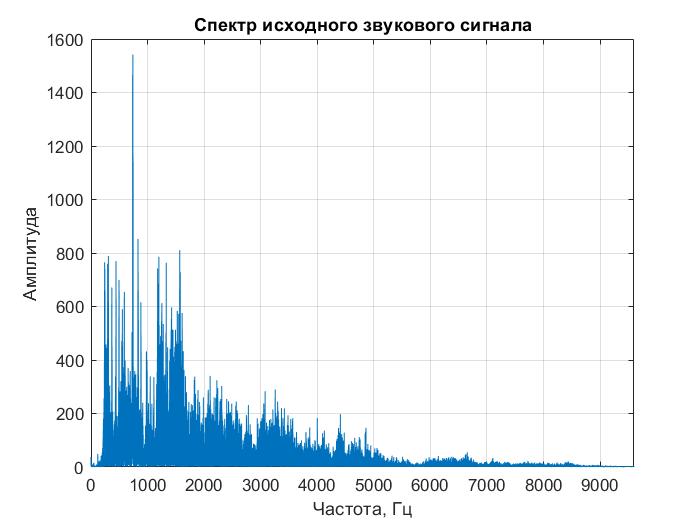
Рисунок 2.2 – Спектр исходного звукового сигнала
Далее, с помощью фильтра Баттерворта, спроектируем высокочастотный фильтр в среде Matlab. АЧХ и ФЧХ фильтра представлены на рисунке 2.3.
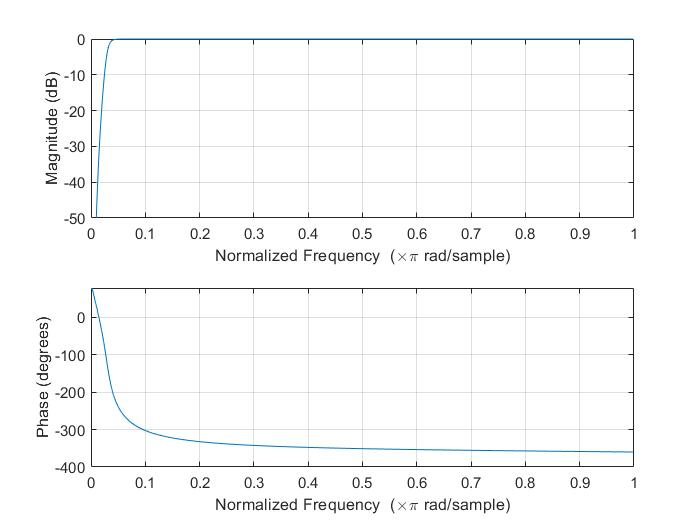
Рисунок 2.3 – АЧХ и ФЧХ ВЧ фильтра Баттерворта
Спектр звукового сигнала на выходе фильтра представлен на рисунке 2.4. Масштаб графика взят в соответствии со спектром исходного звукового сигнала, представленного на рисунке 2.1.
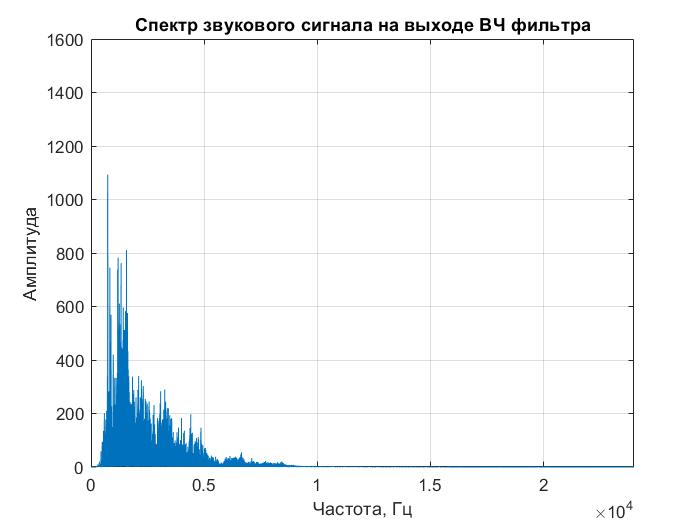
Рисунок 2.4 – Спектр звукового сигнала на выходе ВЧ фильтра Баттерворта
Таким же образом, с помощью фильтра Баттерворта, спроектируем НЧ фильтр в среде Matlab. АЧХ и ФЧХ фильтра представлены на рисунке 2.5.
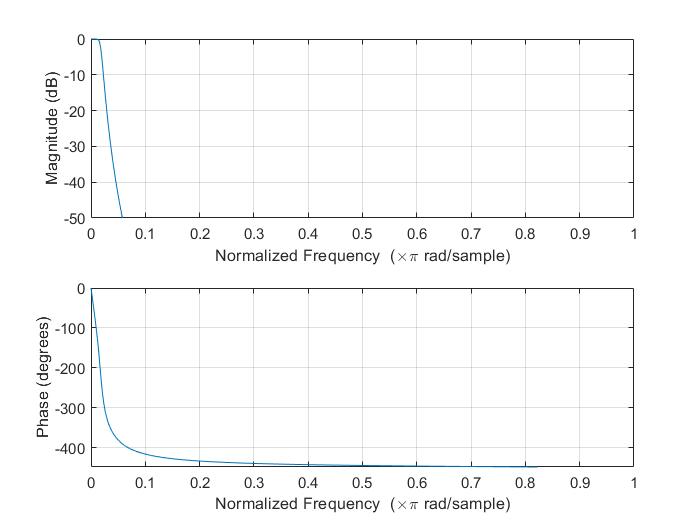
Рисунок 2.5 – АЧХ и ФЧХ НЧ фильтра Баттерворта
Спектр звукового сигнала на выходе фильтра представлен на рисунке 2.6.
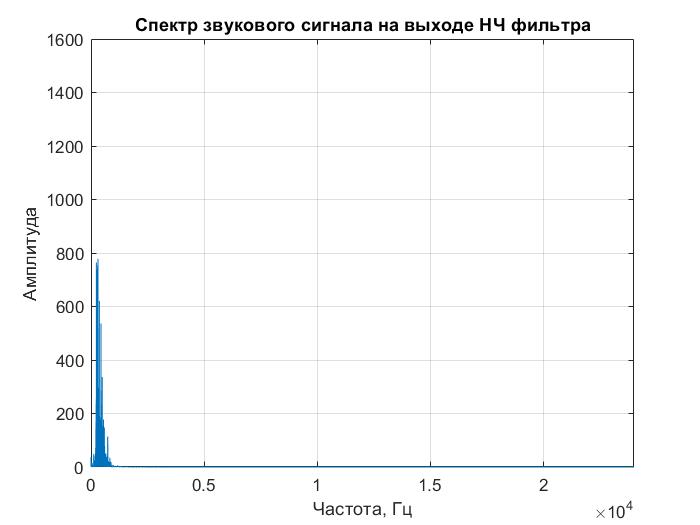
Рисунок 2.6 – Спектр звукового сигнала на выходе НЧ фильтра Баттерворта
Листинг программы представлен ниже:
clc, close all, clear all
filename='Music.aac';
[Audio, Fs]=audioread(filename);
Time=(1:length(Audio))*1/Fs; %Зная частоту дискретизации и количество точек, рассчитываем вектор времени
plot(Time, Audio'), grid on %Строим временной график сигнала
title(['Исходный звуковой сигнал (Fs=48000 кГц)'])
xlabel('Время, с')
ylabel ('Амплитуда, В')
[f1,Shift1]=FFT(Fs,Audio);
xlim([0 Fs/5])
title(['Спектр исходного звукового сигнала'])
hold on
%%% ВЧ фильтрация
figure
freq_sreza=740;
[b,a]=butter(5, freq_sreza/(Fs/2),'high');
freqz(b,a);
ylim([-50 0])
Audio1=filter(b,a,Audio);
[f2,Shift2]=FFT(Fs,Audio1);
xlim([0 Fs/2]);
ylim([0 1600]);
title(['Спектр звукового сигнала на выходе ВЧ фильтра'])
%%% НЧ фильтрация
figure
freq_sreza=440;
[b,a]=butter(5, freq_sreza/(Fs/2));
freqz(b,a);
ylim([-50 0])
Audio2=filter(b,a,Audio);
[f2,Shift2]=FFT(Fs,Audio2);
xlim([0 Fs/2]);
ylim([0 1600]);
title(['Спектр звукового сигнала на выходе НЧ фильтра'])
sound(Audio2,Fs);
Выводы
АЧХ фильтра Баттерворта максимально гладкая на частотах полосы пропускания и снижается практически до нуля на частотах полосы подавления. При отображении частотного отклика фильтра Баттерворта на логарифмической АФЧХ, амплитуда снижается к минус бесконечности на частотах полосы подавления.
В сравнении с фильтрами Чебышёва I и II типов или эллиптическим фильтром, фильтр Баттерворта имеет более пологий спад характеристики и поэтому должен иметь больший порядок (что более трудно в реализации) для того, чтобы обеспечить нужные характеристики на частотах полосы подавления. Однако фильтр Баттерворта имеет более линейную фазо-частотную характеристику на частотах полосы пропускания.