ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 12.01.2024
Просмотров: 64
Скачиваний: 1
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
1) Умножаем матрицы, (XT*Y)
| XT Y = |
|
Находим обратную матрицу (XTX)-1
| (XT X) -1 = |
|
Вектор оценок коэффициентов регрессии равен
| Y(X) = |
| * |
| = |
|
Уравнение регрессии (оценка уравнения регрессии): Y = 98.3467 + 9.22X1-0.1667X2
Константа оценивает агрегированное влияние прочих (кроме учтенных в модели хi) факторов на результат Y и означает, что Y при отсутствии xi составила бы 98.3467. Коэффициент b1 указывает, что с увеличением x1 на 1, Y увеличивается на 9.22. Коэффициент b2 указывает, что с увеличением x2 на 1, Y снижается на 0.1667.
2) Найдем парные коэффициенты корреляции.
Значения парного коэффициента корреляции свидетельствует о весьма сильной линейной связи между x1 и y.
Значения парного коэффициента корреляции свидетельствует о весьма сильной линейной связи между x2 и y.
Значения парного коэффициента корреляции свидетельствует о весьма сильной линейной связи между x2 и x1.
Матрица парных коэффициентов корреляции R:
| - | y | x1 | x2 |
| y | 1 | 0.9999 | 0.9938 |
| x1 | 0.9999 | 1 | 0.9948 |
| x2 | 0.9938 | 0.9948 | 1 |
Частные коэффициенты корреляции:
3) Модель регрессии в стандартном масштабе:
rx1y=β1+rx1x2•β2 + ... + rx1xm•βm
rx2y=rx2x1•β1 + β2 + ... + rx2xm•βm
...
rxmy=rxmx1•β1 + rxmx2•β2 + ... + βm
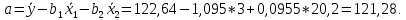
Стандартизированная форма уравнения регрессии имеет вид:
ty = 121.28 + 1.095x1 -0.0955x2
4) Коэффициенты в стандартизованном масштабе удовлетворяют неравенству 2 1, т.е. фактор x1 оказывает более сильное влияние на результат y по сравнению с фактором x2 .
5) Средняя ошибка аппроксимации
6)
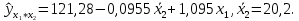
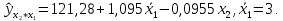
или
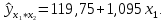
7) Частные коэффициенты эластичности:
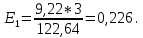При изменении фактора х1 на 1%, Y изменится на 0.226%. Частный коэффициент эластичности |E1| < 1. Следовательно, его влияние на результативный признак Y незначительно.
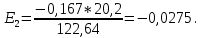При изменении фактора х2 на 1%, Y изменится на -0.0275%.8) Множественный коэффициент корреляции (Индекс множественной корреляции):
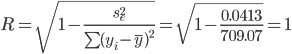
или
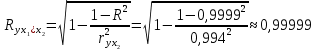
Оба показателя близки к 1.
9) Критерий F-Фишера.
F-статистика. Критерий Фишера.
Если F < Fkp = Fα ; n-m-1, то нет оснований для отклонения гипотезы H0.
F
=
=
=17153.968
Табличное значение при степенях свободы k1 = 2 и k2 = n-m-1 = 5 - 2 - 1 = 2, Fkp(2;2) = 99
Поскольку фактическое значение F > Fkp, то коэффициент детерминации статистически значим и уравнение регрессии статистически надежно (т.е. коэффициенты bi совместно значимы).
10) Оценим с помощью частного F-критерия:
1) целесообразность включения в модель регрессии факторов х1 после введения хj (Fx1).
Определим наблюдаемое значение частного F-критерия:
Fx1=
R2(x2,xn) = r2(x2) = 0.99382 = 0.988
Fkp(k1=1;k2=2) = 98.5
Сравним наблюдаемое значение частного F-критерия с критическим:
Fx1>98.5, следовательно, фактор х1 целесообразно включать в модель после введения фактора х2.
2) целесообразность включения в модель регрессии факторов х2 после введения хj (Fx2).
Определим наблюдаемое значение частного F-критерия:
Fx2=
R2(x1,xn) = r2(x1) = 0.99992 = 1
Сравним наблюдаемое значение частного F-критерия с критическим:
Fx2<98.5, следовательно, фактор х2 не целесообразно включать в модель после введения фактора х1.
11) t-статистика:
Tтабл (n-m-1;α/2) = (2;0.005) = 14.089
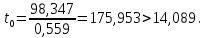Статистическая значимость коэффициента регрессии b0 подтверждается.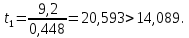
Статистическая значимость коэффициента регрессии b1 подтверждается.
Статистическая значимость коэффициента регрессии b2 не подтверждается.
12) Y(3.15,21.21) = 98.35 + 9.22*3.15-0.167*21.21 = 123.855
V = X0T(XTX)-1X0
где
| X0 = |
|
X0T = [ 1 ; 3.15 ; 21.21]
| (XT X) -1 = |
|