Добавлен: 12.01.2024
Просмотров: 48
Скачиваний: 2
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
3.1. Виды дополнительной работы с решенной текстовой задачей.
-
изменение условия так, чтобы задача решалась другим действием; -
постановка нового вопроса к уже решенной задаче, ответ на который можно найти по данному условию -
сравнение содержания данной задачи и ее решения с содержанием и решением другой задачи; -
решение задачи другим способом или с помощью других средств – другим методом: графическим, алгебраическим и т.д.); -
изменение числовых данных задач так, чтобы появился другой способ решения или, наоборот, чтобы один из способов решения стал невозможным; -
исследование решения. Сколько способов решения имеет задача? При каких условиях она не имела бы решения? Какие приемы наиболее целесообразны для поиска решения этой задачи? Возможны ли другие методы решения?; -
обоснование правильности решения (проверка).
Из этого следует, что необходимо с первого класса учить детей разбивать текст на смысловые части и моделировать ситуации, отраженные в текстовой задаче.
Предметное и графическое моделирование математической ситуации при решении текстовых задач давно применяется в школьной практике, но без должной системы и последовательности, что объясняется неправильным пониманием роли наглядности в обучении и развитии учащихся. Как отмечает Л.Ш. Левенберг, «рисунки, схемы и чертежи не только помогают учащимся в сознательном выявлении скрытых зависимостей между величинами, но и побуждают активно мыслить, искать наиболее рациональные пути решения задач, помогают не только усваивать знания, но и овладевать умением применять их».
Как доказательство, можно привести следующие примеры:
Во 2 классе, впервые анализируя задачу
«В первый день для ремонта школы привезли 28 бревен, а во второй день привезли на 4 машинах по 10 бревен. Сколько всего бревен привезли за эти 2 дня?», обычно записывают ее кратко в таком виде:
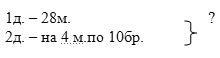
Такая модель не отражает жизненной ситуации с достаточной наглядностью, что и приводит к ошибкам в решении задачи. Необходимо смоделировать ее условие в виде схематического рисунка:
Такая модель отражает математическую ситуацию более наглядно. Возникает запись решения задачи:
28 + 10 * 4=68 (бр.) или
1) 10 +10 +10 +10 = 40(бр.)
2)28 + 40 = 68(бр.)
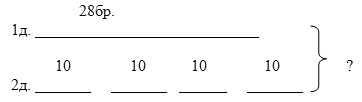
А при таком моделировании выбор действий будет понятным и обоснованным, учащиеся не будут действовать наугад, механически манипулируя числами.
Автор учебников математики для начальной школы Н.Б.Истомина выделяет 4 основных способа решения текстовых задач:
-
Практический -
Арифметический -
Алгебраический -
Графический
Сущность каждого из способов покажем на решении следующей задачи:
«В гараже стояло 10 машин. После того, как несколько машин уехало, осталось 6. Сколько машин уехало из гаража?»
Четыре стандартных способа решения.
-
Практический

Возможности этого метода ограничены, поскольку дети могут выполнять предметные действия только с небольшими количествами.
-
Арифметический
10 – 6 = 4 (м) – уехавшие машины
-
Алгебраический
Пусть х – уехавшие машины. Тогда количество всех машин можно записать выражением:
6 + х – все машины
По условию задачи известно, что всего в гараже стояло 10 машин. Значит:
6 + х = 10
Решив это уравнение, мы ответим на вопрос задачи.
-
Графический
В момент решения этот способ является свернутым практическим, т.к. арифметическое решение опирается на осознание - во внутреннем плане действий – понятий суммы и слагаемых, т.е. на глубокое понимание смысла вычитания как нахождения неизвестного слагаемого. А буквально через несколько минут решение задачи превращается в числовой пример. И как-то уходит из поля зрения и учителя и ученика то, для решения текстовой задачи самым главным было не написать (10 – 6), а проанализировать условие: выявить имеющиеся данные и их взаимосвязи, понять вопрос и только после этого получить возможность осознать – какими арифметическими средствами получить решение.
Н.Б.Истомина пишет: «…все многообразие методических рекомендаций, связанных с обучением младших школьников с обучением задач, целесообразно рассматривать с точки зрения двух принципиально отличающихся друг от друга подходов. Один из них нацелен на формирование у учащихся умения решать задачи определенных типов…
Цель другого подхода – научить детей выполнять семантический анализ текстовых задач, выявлять взаимосвязи между условием и вопросом, данными и искомыми, представлять эти связи в виде схематических и символических моделей».
В методической литературе выделяют четыре основных этапа решения текстовой задачи:
-
восприятие и осмысление задачи; -
поиск плана решения; -
выполнение плана решения; -
проверка решения.
1 этап – восприятие задачи.
«В одной корзине лежало 24 кг яблок, а в другой лежали груши. Когда в корзину с грушами положили еще 8 кг груш, их стало на 10 кг больше, чем яблок. Сколько килограммов груш было в корзине?»
| учитель | ученик |
| Докажи, что этот текст является задачей. | Есть условие и вопрос. Данные известные и неизвестные. |
| Выполни иллюстрацию и схематический чертеж. | 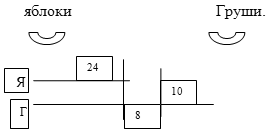 |
| Попробуй сделать краткую запись задачи. | Я. – 24 кг Гр. – ? +8, на 10кг больше. |
| Выбери неизвестное и обозначь его буквой. | Х – было груш (х+8) – стало груш (х+8) – 10 – груш столько же, сколько яблок. Т.к. известно, что яблок 24 кг, то можно составить уравнение |
2 этап – поиск решения задачи.
| учитель | ученик |
| Найди план решения задачи по чертежу. | Искомый отрезок на чертеже длиннее отрезка, изображающего количество яблок на величину отрезка, который является разницей между отрезками, обозначающими 10кг и 8 кг Значит, надо сначала найти разность между 10 и 8, потом ее прибавить к 24 и найти искомое число. |
| Запиши рассуждения: -на сколько груш стало больше, чем яблок? - сколько было яблок? - сколько добавили груш? -сколько груш стало? | Чтобы узнать, сколько груш было, надо знать, сколько груш стало (?) и сколько добавили груш (8) Чтобы узнать, сколько груш стало, надо знать, на сколько груш больше, чем яблок (10кг) и сколько яблок (24кг) |
| Составь уравнение, которое является планом решения задачи. | Так как яблок было 24кг, а величина, выраженная в килограммах и равная этой, записана выражением (х+8)-10, то можно составить уравнение (х + 8) – 10 = 24 |
3 этап – выполнение плана решения.
-
Арифметический
1 способ:
-
24 + 10 = 34 (кг) -
34 – 8 =26 (кг)
2 способ:
1) 10 – 8 = 2 (кг)
2) 24 + 2 = 26 (кг)
Формы записи можно оформить и с пояснениями и выражением
(24 +10) – 8 = 26
-
Алгебраический
(Х + 8) – 10 = 24
Х +8 = 24 + 10
Х = 34 – 8
Х = 26
4 этап – проверка решения.
| учитель | ученик |
| Выполни проверку решения задачи одним из способов. | Подставим полученный результат(26) в условие задачи и проверим полученный текст на наличие противоречий. « В одной корзине лежало 24 кг яблок, а в другой лежало 26 кг груш. Когда в корзину с грушами положили еще 8 кг груш, их стало на 10 кг больше, чем яблок». В данном тексте противоречий нет. |
Формулировка ответа к задаче:
«Ответ: 26 кг груш было в корзине».
Составление обратной задачи:
« В одной корзине лежали яблоки, а в другой 26 кг груш. Когда в корзину с грушами положили еще 8 кг груш, их стало на 10 кг больше, чем яблок. Сколько килограммов яблок было в корзине?»
Сравнив ответ, полученный для обратной задачи, мы увидим, что между ними нет противоречий. Значит, задача была решена верно.
Заключение.
Работа над текстовой задачей остается одним из важнейших аспектов обучения в начальной школе, когда закладываются основы знаний; является движущим фактором в развитии младших школьников. Из текстов задач дети открывают новое об окружающем мире, испытывают чувство удовлетворения и радости от их успешного решения.
Решение текстовых задач и нахождение разных способов их решения на уроках математики способствует развитию у детей мышления, памяти, внимания, творческого воображения, наблюдательности, последовательности рассуждения и его доказательности, развитию умения кратко, четко и правильно излагать свои мысли.