Файл: Отчет по лабораторной работе 2 Вариант 5 по дисциплине Физика конденсированного состояния.docx
Добавлен: 12.01.2024
Просмотров: 59
Скачиваний: 2
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
Министерство науки и высшего образования Российской Федерации
Федеральное государственное бюджетное образовательное учреждение высшего образования
ТОМСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ СИСТЕМ УПРАВЛЕНИЯ И РАДИОЭЛЕКТРОНИКИ (ТУСУР)
Кафедра промышленной электроники (ПрЭ)
Физика конденсированного состояния
ОТЧЕТ
по лабораторной работе №2 Вариант №5
по дисциплине «Физика конденсированного состояния»
Студент гр № з-511П12-5
Д. Р. Хисматуллин
«23» марта 2023 г
Томск 2023
Задание
Пусть дан образец кремния (Si), легированного бором (В). Данный полупроводник имеет удельное сопротивление 5 Ом см ⋅ и линейные размеры a=1 мм, d=1мм, l=10 мм и нагрет с одной стороны до 300 К, а с другой стороны до 350 К.
Решение
Для кремния бор является донорной примесью, следовательно, данный образец — полупроводник n-типа.
Среднюю концентрацию носителей заряда (
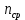 ) определим из электропроводности полупроводника:
) определим из электропроводности полупроводника: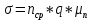
где
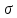 — электропроводность полупроводника,
— электропроводность полупроводника,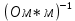 ;
; 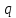 — заряд электрона,
— заряд электрона,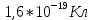 ;
; 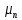 — подвижность носителей заряда (в данном случае, электронов),
— подвижность носителей заряда (в данном случае, электронов), 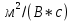
Электропроводность полупроводника рассчитаем по формуле:
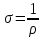
где ρ — удельное сопротивление полупроводника,
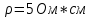
Температурная зависимость подвижности электронов (μ) изменяется по закону:
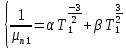
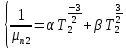
где
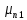 — подвижность электронов при
— подвижность электронов при 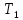 ;
; 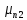 — подвижность электронов при
— подвижность электронов при 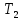 ; α, β — некоторые параметры полупроводника.
; α, β — некоторые параметры полупроводника.Слагаемое
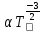 соответствует области низких температур, где преобладает рассеяние носителей заряда на ионах примеси. Слагаемое
соответствует области низких температур, где преобладает рассеяние носителей заряда на ионах примеси. Слагаемое 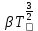 соответствует области высоких температур, где преобладает рассеяние носителей заряда тепловых колебаний решетки (фононах).
соответствует области высоких температур, где преобладает рассеяние носителей заряда тепловых колебаний решетки (фононах).Для заданного диапазона температур (300 - 350 К) можно пренебречь рассеянием носителей заряда на ионах примеси и учитывать только второе слагаемое в формуле —
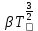 . Тогда выражение можно записать следующим образом:
. Тогда выражение можно записать следующим образом: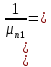
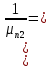
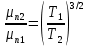
Таким образом, подвижность электронов (
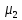 ) при
) при 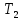 :
: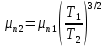
где
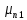 — подвижность электронов при
— подвижность электронов при 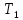 = 300 К, для Si
= 300 К, для Si 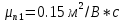
Среднюю концентрацию и подвижность носителей заряда найдем при средней температуре (
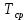 ):
):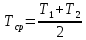
В данном случае
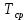 будет равна:
будет равна: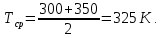
Подвижность носителей заряда (
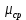 ) при
) при 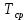 равна:
равна: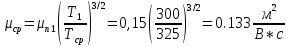
Запишем выражение для
 :
: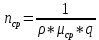
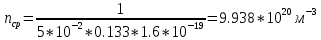
Разность потенциалов на концах образца полупроводника (
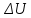 ) можно определить по формуле:
) можно определить по формуле: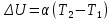
где
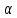 — дифференциальная термо-ЭДС, В/К.
— дифференциальная термо-ЭДС, В/К.Дифференциальная термо-ЭДС
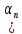 ) для полупроводника n-типа определяется выражением:
) для полупроводника n-типа определяется выражением: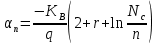
Где
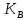 — постоянная Больцмана,
— постоянная Больцмана,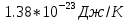 ; r — фактор рассеяния, определяемый механизмом рассеяния носителей заряда, в диапазоне температур (300-350 )К рассеяние происходит на акустических колебания кристаллической решетки, поэтому r = 0;
; r — фактор рассеяния, определяемый механизмом рассеяния носителей заряда, в диапазоне температур (300-350 )К рассеяние происходит на акустических колебания кристаллической решетки, поэтому r = 0; 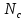 — эффективная плотность состояний в зоне проводимости,
— эффективная плотность состояний в зоне проводимости, 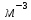
Эффективная плотность состояний (
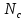 ) рассчитывается по формуле:
) рассчитывается по формуле: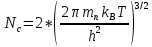
Где
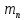 — эффективная масса электронов, для Si
— эффективная масса электронов, для Si 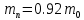 ;
;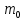 — масса электрона в состоянии покоя,
— масса электрона в состоянии покоя,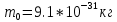 ; h — постоянная Планка,
; h — постоянная Планка, 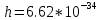 Дж *с.
Дж *с.Рассчитаем
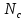 при
при 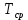 :
: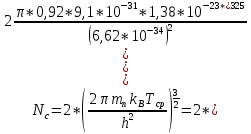
Рассчитаем
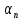 :
: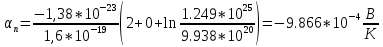
Рассчитаем
 :
:
Диффузионная плотность тока (
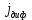 ) для полупроводника n-типа определяется выражением:
) для полупроводника n-типа определяется выражением: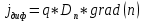
где
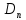 — коэффициент диффузии электронов,
— коэффициент диффузии электронов,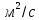 ; grad(n) — градиент концентрации электронов,
; grad(n) — градиент концентрации электронов,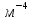 .
.Коэффициент диффузии (
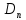 ) определяется из соотношения Эйнштейна:
) определяется из соотношения Эйнштейна: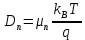
Рассчитаем
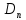 при
при  :
: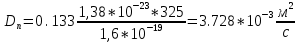
Градиент концентрации grad(n) определяется по формуле:
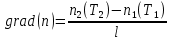
где
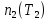 — концентрация электронов при
— концентрация электронов при  ;
; 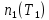 — концентрация электронов при
— концентрация электронов при  ;
; 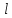 — длина образца полупроводника, м.
— длина образца полупроводника, м.Рассчитаем
 при
при  :
: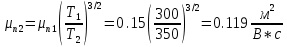
Рассчитаем
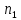 и
и 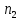 при
при  и
и  :
: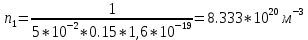
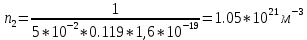
Рассчитаем grad(n):
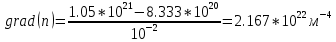
Рассчитаем
 :
: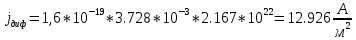
Диффузионный ток
 определяется как:
определяется как: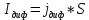
где S — площадь образца полупроводника,S=a*d=
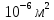 .
.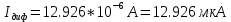
Дрейфовая плотность тока (
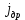 ) полупроводника n -типа определяется выражением:
) полупроводника n -типа определяется выражением: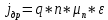
где
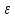 — напряженность электрического поля, В/м.
— напряженность электрического поля, В/м.Напряженность электрического поля
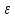 определяется по формуле:
определяется по формуле: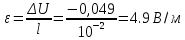
Рассчитаем
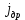 при
при  :
: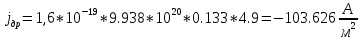
Рассчитаем
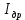 :
: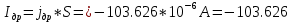
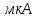
Коэффициент Холла (
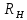 ) для полупроводника n-типа рассчитывается по формуле:
) для полупроводника n-типа рассчитывается по формуле: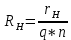
где
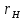 — Холл-фактор, который определяется механизмом рассеяния носителей заряда, в диапазоне температур (300 - 350 ) К рассеяние происходит на акустических колебаниях кристаллической решетки, поэтому
— Холл-фактор, который определяется механизмом рассеяния носителей заряда, в диапазоне температур (300 - 350 ) К рассеяние происходит на акустических колебаниях кристаллической решетки, поэтому 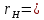 1,18.
1,18.Рассчитаем
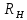 при
при 