Файл: Отчет по лабораторной работе 3 Исследование процессов заряда и разряда конденсатора.docx
Добавлен: 12.01.2024
Просмотров: 710
Скачиваний: 58
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
ПЕРВОЕ ВЫСШЕЕ ТЕХНИЧЕСКОЕ УЧЕБНОЕ ЗАВЕДЕНИЕ РОССИИ
| |  | |
МИНИСТЕРСТВО НАУКИ И ВЫСШЕГО ОБРАЗОВАНИЯ РОССИЙСКОЙ ФЕДЕРАЦИИ
Федеральное государственное бюджетное образовательное учреждение высшего образования
«САНКТ-ПЕТЕРБУРГСКИЙ ГОРНЫЙ УНИВЕРСИТЕТ»
Кафедра общей и технической физики
ЭЛЕКТРИЧЕСТВО
Отчет по
лабораторной работе № 3
«Исследование процессов заряда и разряда конденсатора»
Выполнил: студент гр. АПН-22_________ /Пудов М.Д./
(подпись) (Ф.И.О.)
Оценка:______
Дата:_________
Проверил: ________ / /
(должность) (подпись) (Ф.И.О.)
Санкт-Петербург
2023
Цель работы: 1)Экспериментальная проверка экспоненциального характера процессов заряда и разряда конденсатора. 2)Экспериментальное определение постоянной времени RC-цепи
Краткое теоретическое содержание:
Явление, изучаемое в работе: заряд и разряд конденсатора.
Определения основных физических понятий, объектов, процессов и величин:
Электроемкость (емкость) проводника – коэффициент пропорциональности, равный отношению накопленного на проводнике заряда к его потенциалу, [С]=Ф.
Электроемкость конденсатора – физическая величина, равная отношению накопленного заряда к разности потенциалов между обкладками конденсатора, [С]=Ф.
Конденсатор - система из двух изолированных друг от друга проводников, называющихся пластинами (обкладками)
Законы и соотношения, описывающие изучаемые процессы, на основании которых получены расчетные формулы. Пояснения к физическим величинам и их единицы измерений.
Закон Ома - сила тока в проводнике прямо пропорциональна напряжению на его концах и обратно пропорциональна сопротивлению этого проводника.
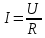 ,
,где I – сила тока, [I]=А; U – напряжение, [U]=В; R – сопротивление, [R]=Ом.
Второе правило Кирхгофа - суммы произведений алгебраических величин сил тока на внешние и внутренние сопротивления всех участков замкнутого контура равны алгебраической сумме величин сторонних электродвижущих сил (ЭДС)
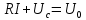 ,
,где I – мгновенное значение силы тока в цепи, [I]=А; UС – мгновенное значение напряжения на конденсаторе, [UС]=В; R – сопротивление, [R]=Ом; U0 - электродвижущая сила (ЭДС) ,[U0] = В.
Схема установки:
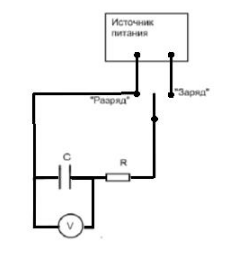
Основные расчетные формулы:
Напряжение на конденсаторе, [UС] = В (при заряде конденсатора)
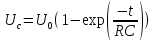 ,
,где U0 - электродвижущая сила (ЭДС) ,[U0] = В; t - время, [t] = с; R - сопротивление, [R] = Ом; C - электроемкость конденсатора, [C] = Ф.
Напряжение на конденсаторе, [UС] = В (при разряде конденсатора)
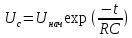 ,
,где Uнач - напряжение на конденсаторе перед его разрядом, [Uнач] = В; t - время, [t] = с; R - сопротивление, [R] = Ом; C - электроемкость конденсатора, [C] = Ф.
Постоянная времени RC – цепи,
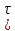 ]=с
]=с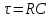 ,
,где R - сопротивление, [R] = Ом; C- электроемкость конденсатора, [C] = Ф
Табличные данные:
| t,с | 0 | 5 | 10 | 15 | 20 | 25 | 30 | 35 | 40 | 45 | 50 | 55 | 60 |
| Uc, В | 0 | 1,09 | 2,05 | 2,91 | 3,74 | 4,45 | 5,13 | 5,64 | 6,19 | 6,70 | 7,15 | 7,53 | 7,90 |
| Uc теор, В | 0 | 1,22 | 2,30 | 3,31 | 4,19 | 4,99 | 5,71 | 6,35 | 6,93 | 7,46 | 7,92 | 8,35 | 8,72 |
| In(Umax-Uc) | 2,47 | 2,38 | 2,29 | 2,20 | 2,11 | 2,01 | 1,93 | 1,83 | 1,74 | 1,65 | 1,56 | 1,47 | 1,38 |
| 70 | 80 | 90 | 100 | 110 | 120 | 130 | 140 | 150 | 160 | 170 | 180 | 190 |
| 8,58 | 9,09 | 9,59 | 9,96 | 10,27 | 10,52 | 10,75 | 10,95 | 11,09 | 11,24 | 11,35 | 11,45 | 11,54 |
| 9,37 | 9,89 | 10,32 | 10,66 | 10,93 | 11,16 | 11,34 | 11,48 | 11,60 | 11,70 | 11,77 | 11,84 | 11,89 |
| 1,19 | 1,02 | 0,85 | 0,68 | 0,51 | 0,33 | 0,16 | -0,01 | -0,19 | -0,36 | -0,53 | -0,71 | -0,89 |
| 200 | 210 | 220 | 230 | 240 | 250 | 260 | 270 | 280 | 290 | 300 |
| 11,6 | 11,66 | 11,72 | 11,76 | 11,79 | 11,83 | 11,84 | 11,86 | 11,87 | 11,9 | 11,92 |
| 11,93 | 11,96 | 11,99 | 12,01 | 12,03 | 12,04 | 12,05 | 12,06 | 12,07 | 12,07 | 12,08 |
| -1,08 | -1,27 | -1,47 | -1,71 | -1,90 | -2,21 | -2,53 | -2,81 | -3,22 | -3,91 | -3,91 |
Таблица 1.1. Результаты измерения заряда конденсатора
| t,с | 0 | 5 | 10 | 15 | 20 | 25 | 30 | 35 | 40 | 45 | 50 | 55 | 60 |
| Uc, В | 12,01 | 11,01 | 10,1 | 9,16 | 8,39 | 7,65 | 7,01 | 6,46 | 5,9 | 5,44 | 4,97 | 4,54 | 4,15 |
| Uc теор, В | 11,86 | 10,66 | 9,59 | 8,62 | 7,75 | 6,97 | 6,26 | 5,63 | 5,06 | 4,55 | 4,09 | 3,68 | 3,31 |
| In(U0/Uc) | 0 | 0,09 | 0,18 | 0,28 | 0,36 | 0,44 | 0,53 | 0,63 | 0,72 | 0,81 | 0,89 | 0,98 | 1,07 |
| 70 | 80 | 90 | 100 | 110 | 120 | 130 | 140 | 150 | 160 | 170 | 180 | 190 | 200 |
| 3,49 | 2,95 | 2,48 | 2,08 | 1,80 | 1,5 | 1,29 | 1,1 | 0,94 | 0,79 | 0,68 | 0,58 | 0,49 | 0,42 |
| 2,67 | 2,16 | 1,75 | 1,41 | 1,14 | 0,92 | 0,75 | 0,60 | 0,49 | 0,39 | 0,32 | 0,26 | 0,21 | 0,17 |
| 1,24 | 1,42 | 1,59 | 1,76 | 1,93 | 2,09 | 2,27 | 2,43 | 2,60 | 2,76 | 2,92 | 3,09 | 3,25 | 3,39 |
| 210 | 220 | 230 | 240 | 250 | 260 | 270 | 280 | 290 | 300 |
| 0,36 | 0,31 | 0,27 | 0,23 | 0,20 | 0,17 | 0,15 | 0,13 | 0,12 | 0,10 |
| 0,14 | 0,11 | 0,09 | 0,07 | 0,06 | 0,05 | 0,04 | 0,03 | 0,02 | 0,02 |
| 3,55 | 3,71 | 3,86 | 3,99 | 4,13 | 4,31 | 4,44 | 4,59 | 4,68 | 4,78 |
Таблица 2.1. Результаты измерения разряда конденсатора
| t,с | 0 | 5 | 10 | 15 | 20 | 25 | 30 | 35 | 40 | 45 | 50 | 55 |
| Uc, В | 0 | 0,12 | 0,24 | 0,35 | 0,46 | 0,57 | 0,67 | 0,78 | 0,89 | 0,99 | 1,10 | 1,20 |
| Uc теор, В | 0 | 0,15 | 0,35 | 0,47 | 0,53 | 0,65 | 0,74 | 0,86 | 0,98 | 1,10 | 1,25 | 1,28 |
| In(Umax-Uc) | 2,38 | 2,20 | 1,99 | 1,80 | 1,64 | 1,46 | 1,28 | 1,08 | 0,92 | 0,74 | 0,57 | 0,40 |
| 60 | 70 | 80 | 90 | 100 | 110 | 120 | 130 | 140 | 150 | 160 | 170 | 180 | 190 |
| 1,29 | 1,5 | 1,7 | 1,88 | 2,06 | 2,25 | 2,42 | 2,6 | 2,73 | 2,93 | 3,09 | 3,24 | 3,58 | 3,69 |
| 1,45 | 1,67 | 1,92 | 2 | 2,23 | 2,47 | 2,59 | 2,76 | 2,92 | 3,08 | 3,24 | 3,58 | 3,68 | 3,9 |
| 0,24 | -0,17 | -0,45 | -0,76 | -1,08 | -1,39 | -1,71 | -1,97 | -2,30 | -2,53 | -2,81 | -2,22 | -2,51 | -2,91 |