Файл: Контрольная работа по дисциплине Статистика Вариант 2 Выполнила студентка группы.docx

Скачать файл (0,18Мб)

Заказать решение

ВУЗ: Не указан

Категория: Не указан

Дисциплина: Не указана

Добавлен: 12.01.2024

Просмотров: 50

Скачиваний: 1

ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.

ГОСУДАРСТВЕННАЯ АКАДЕМИЯ ЖИЛИЩНО-КОМУНАЛЬНОГО ХОЗЯЙСТВА

Донецкий институт городского хозяйства

Контрольная работа

по дисциплине «Статистика»

Вариант 2

Выполнила студентка группы ______________

________________________________________

Руководитель ___________________________

Донецк 2008г.

Задача 1
По данным об основных фондах группы промышленных предприятий, за отчетный год, определить:

Среднее значение показателя (среднее арифметическое)
Показатели вариации (размах вариации, среднее линейное отклонение, среднее квадратическое отклонение, дисперсию, коэффициент вариации)

Таблица 1

Исходные данные для задачи 1

Номер предпр

Основные фонды, млн.грн

Номер предпр

Основные фонды, млн.грн

Номер предпр

Основные фонды, млн.грн

Номер предпр

Основные фонды, млн.грн

Номер предпр

Основные фонды, млн.грн

1

2,74

6

2,5

11

0,51

16

2

21

1,78

2

1,47

7

1,26

12

1,18

17

1,04

22

0,89

3

0,76

8

0,64

13

2,18

18

0,44

23

1,66

4

1,35

9

0,58

14

1,1

19

1,87

24

0,82

5

0,68

10

2,32

15

0,35

20

0,96

25

1,56
Решение:

Таблица 2.

Данные для расчета основных статистических показателей

Номер предпр

Основные фонды, млн.грн

Номер предпр

Основные фонды, млн.грн

1

2,74

1,43

2,06

14

1,1

0,21

0,04

2

1,47

0,16

0,03

15

0,35

0,96

0,91

3

0,76

0,55

0,30

16

2

0,69

0,48

4

1,35

0,04

0,00

17

1,04

0,27

0,07

5

0,68

0,63

0,39

18

0,44

0,87

0,75

6

2,5

1,19

1,43

19

1,87

0,56

0,32

7

1,26

0,05

0,00

20

0,96

0,35

0,12

8

0,64

0,67

0,44

21

1,78

0,47

0,23

9

0,58

0,73

0,53

22

0,89

0,42

0,17

10

2,32

1,01

1,03

23

1,66

0,35

0,13

11

0,51

0,80

0,63

24

0,82

0,49

0,24

12

1,18

0,13

0,02

25

1,56

0,25

0,06

13

2,18

0,87

0,76

сумма

32,64

14,14

11,14

Среднее значение показателя

, где

- отдельные значения изучаемого показателя;

n – количество значений показателя.

Размах вариации

, где

- максимальное и минимальное значение показателя

Среднее линейное отклонение

Дисперсия

Среднее квадратическое отклонение

Коэффициент вариации статистического ряда

Т.к. Vx > 15%, то совокупность неоднородная.

Задача 2
По статистическим данным об объеме производства важнейших видов продукции в Украине в 1987-1992 гг., выполнить следующее:

определить уровни ряда динамики по периодам времени, приняв за базисный период 1987г., а затем:

а) поместить значения уровней динамики в таблицу;

б) изобразить ряд динамики графически.

2) определить базисные и цепные абсолютные приросты объема продукции;

3) определить базисные и цепные коэффициенты и темпы роста (динамики);

4) определить базисные и цепные темпы прироста;

5) определить абсолютное значение одного процента прироста объема продукции;

6) определить средний уровень ряда динамики;

7) определить средний темп роста и средний темп прироста объема продукции;

8) определить среднюю величину 1% прироста объема продукции.

Решение

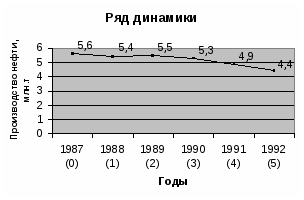1. Данные по нефти

Таблица 3.

Исходные данные для задачи 2.

Годы

Нефть, млн.т

1987 (0)

5,6

1988 (1)

5,4

1989 (2)

5,5

1990 (3)

5,3

1991 (4)

4,9

1992 (5)

4,4
2. Абсолютный прирост

а) базисный

и т.д.

б) цепной

и т.д.

3. Коэффициент роста:

а) базисный

и т.д.

б) цепной

и т.д.

4. Определяем темп роста

а) базисный

и т.д.

б) цепной

и т.д.

5. Темп прироста:

а) базисный

и т.д.

б) цепной

и т.д.

Абсолютное значение 1% прироста

млн.т

млн.т

и т.д.

Занесем полученные данные в таблицу

Таблица 4.

Показатели

1987 (0)

1988 (1)

1989 (2)

1990 (3)

1991 (4)

1992 (5)

Уровень нефти, млн.т

5,6

5,4

5,5

5,3

4,9

4,4

Абсолютный прирост, млн.т

-базисный

0

-0,2

-0,1

-0,3

-0,7

-1,2

-цепной

0

-0,2

0,1

-0,2

-0,4

-0,5

Коэффициент роста

-базисный

0

0,964

0,982

0,946

0,875

0,786

-цепной

0

0,964

1,019

0,964

0,925

0,898

Темпы роста, %

-базисный

0

96,4%

98,2%

94,6%

87,5%

78,6%

-цепной

0

96,4%

101,9%

96,4%

92,5%

89,8%

Темпы прироста, %

-базисный

0

-3,57%

-1,79%

-5,36%

-12,50%

-21,43%

-цепной

0

-3,57%

1,85%

-3,64%

-7,55%

-10,20%

Абсолютная величина 1% прироста, млн.т.

0

0,056

0,054

0,055

0,053

0,049

Средний уровень ряда динамики

Средний темп роста

Средний темп прироста

Среднюю величину 1% прироста

Задача 3

Распределение рабочих машиностроительного завода по уровню заработной платы по данным 10%-го случайного бесповоротного выборочного обследования
Таблица 5

Исходные данные для задачи 3.

Зарплата, грн

Число рабочих, чел.

100-200

16

200-300

48

300-400

30

400-500

28

500-600

20

600-700

8

Итого

150

Определить:

1) размер средней заработной платы завода (с вероятностью 0,683);

2) долю рабочих завода, имеющих заработную плату на уровне средней и выше (с вероятностью 0,997);

3) необходимую численность выборки при определении средней заработной платы, чтобы с вероятностью 0,954 предельная ошибка выборки не превышала 5 грн;

4) необходимую численность выборки при определении доли рабочих , имеющих заработную плату на уровне средней и выше, чтобы с вероятностью 0,954 предельная ошибка выборки не превышала 5%.

Решение

Составим расчетную таблицу

Таблица 6

Расчетная таблица

Зарплата, грн

Число рабочих (f)

Середина интервала (x)

100-200

16

150

2400

-208

43264

692224

200-300

48

250

12000

-108

11664

559872

300-400

30

350

10500

-8

64

1920

400-500

28

450

12600

92

8464

236992

500-600

20

550

11000

192

36864

737280

600-700

8

650

5200

292

85264

682112

Итого

150
53700

2910400
Размер средней заработной платы рабочих завода составит