Практическая работа № 1

ОПРЕДЕЛЕНИЕ ПОКАЗАТЕЛЕЙ БЕЗОТКАЗНОСТИ ПО СТАТИСТИЧЕСКИМ ДАННЫМ

На основе представленных статистических данных провести расчет и анализ показателей надежности серии невосстанавливаемых объектов.

Пример выполнения задания

Исходные данные: Число изделий, поставленных на испытание, N = 1000 изделий. Испытания проводятся в течение 100 часов. Каждые сто часов определялось количество отказов изделий. Результаты испытаний представлены в таблице 1.1.

Задание:

1. Найти статистическую оценку распределения вероятностей отказа Q(t) и безотказной работы P(t).

2. Найти изменение плотности вероятности отказов f(t) и интенсивности отказов λ(t) по времени.

3. Результаты расчета отразить на графиках.

Решение.

1. 
   Определяем количество работоспособных изделий на начало каждого периода по формуле
   

2. 
   Определяем статистическую оценку вероятности безотказной работы на начало каждого периода по формуле
   

3. 
   Определяем количество отказавших деталей нарастающим итогом на конец каждого периода по формуле
   

4. 
   Определяем статистическую оценку вероятности отказа на конец каждого периода по формуле
   

5. 
   Определяем статистическую оценку плотности вероятности отказов по формуле
   

6. 
   Определяем значение интенсивности отказов по формуле
   

7. 
   Результаты расчета для удобства сводим в таблицу 1.1.
   
8. 
   По данным расчета строим графики зависимости расчетных величин по времени (рисунки 1.1, 1.2, 1.3)
   

---

Таблица 1.1 – Результаты расчета статистических оценок показателей безотказности

Временной интервал Δt, час	Количество отказов за данный интервал Δn(t)	Количество работоспособных изделий на конец периода N(t)	Количество отказавших изделий на конец периода	Вероятность безотказной работы на конец периода P(t)	Вероятность отказа на конец периода Q(t)	Плотность вероятности отказов f(t) за период, ·10-2	Интенсивность отказов за период λ(t), ·10-2
0	0	1000	0	1,00	0
0 – 100	50	950	50	0,95	0,05	0,05	0,05
100 – 200	40	910	90	0,91	0,09	0,04	0,04
200 – 300	20	890	110	0,89	0,11	0,02	0,02
300 – 400	20	870	130	0,87	0,13	0,02	0,02
400 – 500	10	860	140	0,86	0,14	0,01	0,01
500 – 600	70	790	210	0,79	0,21	0,07	0,09
600 – 700	110	680	320	0,68	0,32	0,11	0,16
700 – 800	280	400	600	0,4	0,6	0,28	0,70
800 – 900	250	150	850	0,15	0,85	0,25	1,67
900 – 1000	150	0	1000	0	1,00	0,15	Стремится к бесконечности

---

Рисунок 1.1 – График зависимости вероятности безотказной работы и вероятности отказа от времени

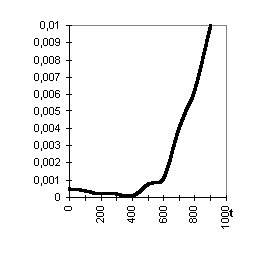Рисунок 1.2 – График зависимости плотности распределения отказов во времени	Рисунок 1.3 – График зависимости интенсивности отказов от времени

Таблица 1.3 – Исходные данные для выполнения домашнего задания по практической работе № 1

Номер варианта	Общее кол-во изделий	Количество отказавших изделий за интервал времени ti, шт.
		0 – 100	100 – 200	200 – 300	300 – 400	400 – 500	500 – 600	600 – 700	700 – 800	800 – 900	900 – 1000
1	1000	30	170	50	20	30	20	280	200	70	130
2	2500	80	320	300	20	80	600	600	110	210	200
3	3000	100	500	200	10	90	100	100	600	100	500
4	5100	150	950	200	100	50	190	1360	1100	250	750
5	1150	50	180	60	20	35	25	330	220	50	170
6	7300	1240	370	140	230	140	2060	1450	450	1000	1240
7	8300	250	1410	420	170	250	160	2320	1660	420	1240
8	300	9	51	15	6	9	6	84	60	15	45
9	1000	30	170	50	30	20	20	180	300	140	60
10	300	9	51	15	9	6	6	54	90	42	18
11	700	22	117	38	20	12	13	143	195	98	42
12	6700	200	1140	260	270	140	134	1206	2010	890	450
13	3700	110	630	190	110	70	80	660	1110	520	220
14	1200	40	200	60	36	24	24	216	360	168	72
15	1800	60	300	90	60	30	36	324	540	252	108
16	1300	34	224	66	30	14	16	276	380	186	74
17	13300	390	2270	510	530	270	258	2402	4010	1770	890
18	7300	210	1250	370	210	130	150	1310	2210	1030	430
19	2300	70	390	110	62	38	38	422	710	326	134
20	3500	110	590	170	110	50	62	638	1070	494	206

---

---

Смотрите также файлы

• Конкурс сочинения Без срока давности.docx

• Инструкция по выполнению работы Тренировочная работа включает в себя 24 задания 16 заданий с кратким ответом и 8 заданий с развёрнутым ответом.pdf

• С. Оушылара нені оыту керектігін малімні тсінуі Д. Оушылара оятын талаптарды малімні білуі Балалар здеріні сеніміне, ьіліміне сйеніп пайымдау жасай алады.docx

• Пояснительная записка Рабочая программа составлена на основе.docx

• аза дебиеті пнінде оушыларды ылымизерттеу дадыларын дамыту Бакмаганбетова Асем Аманкельдыызы Атоай ауданы Сарышаан кенті Сарышаан кентіндегі жалпы орта білім беретін мектеп.docx