Алгебра и начала анализа. 10 класс
Контрольная работа № 6 (Никольский)

Алгебра 10 Никольский Контрольная 6



К-6. Вариант 3 (транскрипт)

1. 
   Упростите выражение: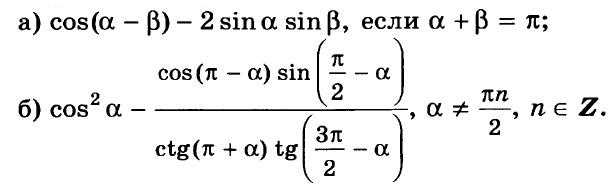
   
   
2. 
   Вычислите (sin 68° + cos 38°)² + (sin 38° – cos 68°)².
   
3. 
   Известно, что cos а = – 5/13, π < а < 3π/2. Вычислите: a) sin a; б) sin 2а; в) cos 2а.
   
4. 
   Постройте график функции у = (sin Зх cos 2х – sin 2х cos Зх) / (cos 3x cos 2х + sin Зх sin 2х).
   
5. 
   * Вычислите 2 cos 37° cos 23° – sin 76°.
   
6. 
   * Докажите справедливость равенства cos π/7 cos 2π/7 cos 4π/7 = –1/8.
   
7. 
   * Велосипедист и мотоциклист одновременно отправились навстречу друг другу из городов Л и В. После встречи мотоциклист прибыл в город В через 1 ч, а велосипедист прибыл в город А через 9 ч. Во сколько раз скорость мотоциклиста больше скорости велосипедиста?
   

К-6. Вариант 4 (транскрипт)

1. 
   Упростите выражение: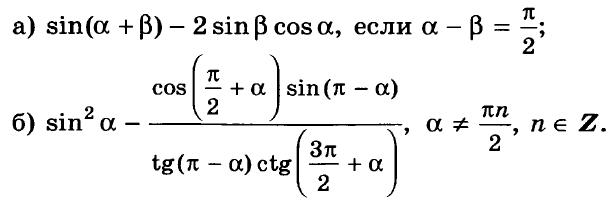
   
   
2. 
   Вычислите (cos 32° + cos 28°)² + (sin 32° – sin 28°)².
   
3. 
   Известно, что sin a = –12/13, 3π/2 < a < 2 π. Вычислите: а) cos а; б) sin 2а; в) cos 2а.
   
4. 
   Постройте график функции у = (cos 4x cos 3x + sin 4x sin 3x) / (sin 4x cos3x – sin 3x cos 4x).
   
5. 
   * Вычислите 2 sin 34° sin 26° – sin 82°.
   
6. 
   * Докажите справедливость равенства cos π/9 cos 2π/9 cos 4π/9 = 1/8.
   
7. 
   * Велосипедист и пешеход одновременно отправились навстречу друг другу из городов А и В. После встречи велосипедист прибыл в город В через 1 ч, а пешеход пришел в город А через 4 ч. Во сколько раз скорость велосипедиста больше скорости пешехода?
   

 

Ответы на контрольную работу




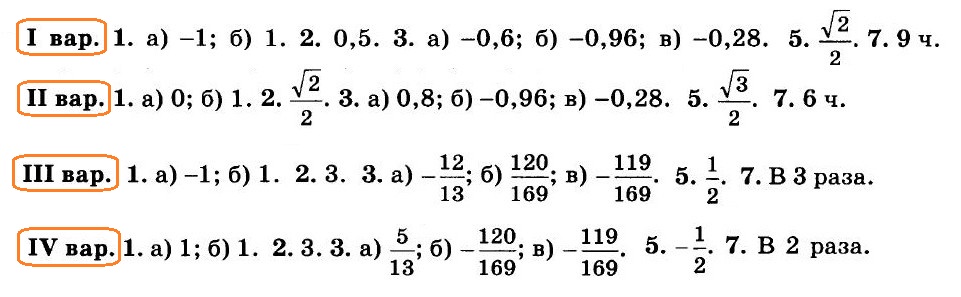
Алгебра и начала анализа. 10 класс
Контрольная работа № 7 (Никольский)

Алгебра 10 Никольский Контрольная 7



К-7. Вариант 3 (транскрипт)

Решите уравнение (1–5).

1. 
   a) cos x = 1; б) sin x = 1/2; в) ctg x = –√3/3.
   
2. 
   а) 2 sin² x + sin x – 1 = 0; б) 3 cos² x – sin x + 1 = 0.
   
3. 
   а) √3 sin x – cos x = 0; б) sin² x + 2√3 sin x cos x + 3 cos² x = 0.
   
4. 
   * a) sin x = –0,6; б) cos x = 2/3; в) tg x = –4.
   
5. 
   * a) sin x + cos x = –1; 6) cos 4x – cos2x = 1.
   
6. 
   * Решите неравенство: a) sin x > –0,5; б) cos x < –0,5; в) tg x ≥ 2.
   
7. 
   * Из города А в город В вышел пешеход. Через некоторое время после выхода пешехода из города В в город А выехал велосипедист, а еще через час вслед за ним выехал мотоциклист. Все участники двигались равномерно и встретились в одной точке маршрута. Пешеход пришел в город В через 6 ч после выезда мотоциклиста, а мотоциклист прибыл в город А через 4 ч после выхода пешехода из города А. Через сколько часов после мотоциклиста велосипедист прибыл в город А?
   

---

К-7. Вариант 4 (транскрипт)

Решите уравнение (1–5).

1. 
   a) sin x = 1; б) cos x = 1/2; в) tg x = –√3/3.
   
2. 
   a) 2 cos² x – cos x – 1 = 0; б) 3 sin² x – 2 cos x + 2 = 0.
   
3. 
   а) √3 sin х + cos x = 0; б) sin² x – 2√3 sin x cos x + 3 cos² x = 0.
   
4. 
   * a) cos x = –0,7; б) sin x = 1/4; в) tg x = 5.
   
5. 
   * a) sin x – cos x = –1; б) cos 4x – sin² x = 1.
   
6. 
   * Решите неравенство: a) sin x < –0,5; б) cos x > –0,5; в) tg x ≤ 2.
   
7. 
   * Из города А в город В вышел пешеход. Через некоторое время после выхода пешехода из города В в город А выехал велосипедист. Через час после выхода пешехода вслед за ним выехал мотоциклист. Все участники двигались равномерно и встретились в одной точке маршрута. Мотоциклист прибыл в город В через 3 ч после выезда из него велосипедиста, но за 2 ч до прибытия пешехода в город В. Через сколько часов после выезда мотоциклиста велосипедист прибыл в город А?
   

 



 

Алгебра 10 класс (Никольский)
Итоговый тест. Вариант 1

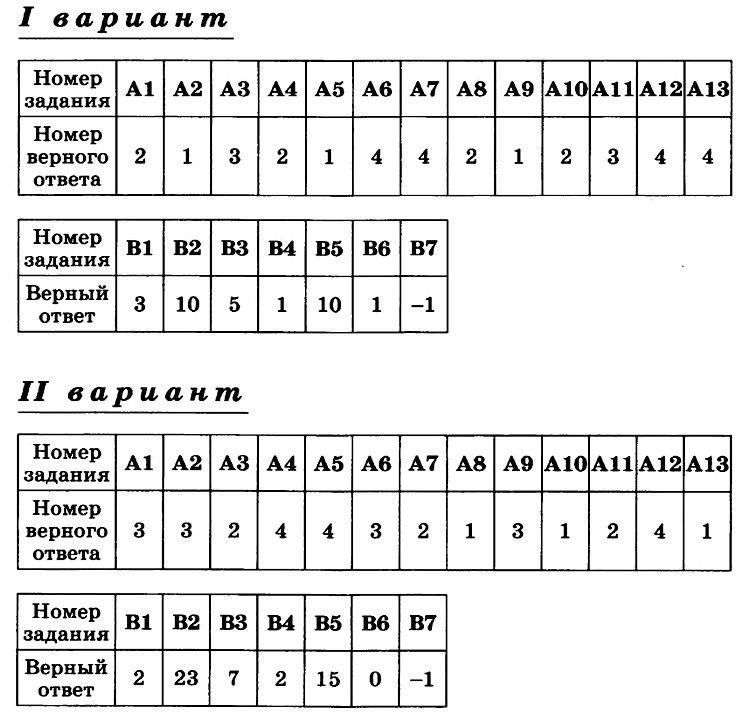
К-8. Вариант 1 (транскрипт)

ЧАСТЬ I. К каждому из заданий А1–А13 дано 4 ответа, из которых только один верный. Для каждого задания запишите номер выбранного вами правильного ответа.

• 
  А1. Упростите выражение ⁴√a : а^–1/2.
  
• 
  А2. Упростите выражение (b^2/5 – 25) / (b^1/5 + 5) – b^1/5.
  
• 
  А3. Упростите выражение log₃ 18 – log₃ 2 + 5^{log5 2}.
  
• 
  А4. Решите неравенство (1/2)^x–2 > 1/8.
  
• 
  А5. Укажите промежуток возрастания функции у = f(x), заданной графиком (рис. 42).
  
• 
  А6. Упростите выражение 2 cos² a/2 – cos а – 1.
  
• 
  А7. Решите уравнение log₂ x = 1/2.
  
• 
  А8. Укажите промежуток, которому принадлежит корень уравнения log₂(x – 2) = 3.
  
• 
  А9. Найдите область определения функции у = √((x – 1)/(x + 1)).
  
• 
  А10. Решите неравенство 9^x ≤ 1/3.
  
• 
  А11. Решите неравенство 2^x+2 + 2^x > 20.
  
• 
  А12. Найдите произведение корней уравнения lg² х – 3 lg х – 10 = 0.
  
• 
  А13. Решите уравнение 2 cos² x – 3 sin x = 0.
  

ЧАСТЬ II. К каждому из заданий В1–В7 укажите полученный вами ответ (только число).

• 
  В1. Найдите сумму корней уравнения 1/(6 • 2^x – 11) = 1/(4^x – 3).
  
• 
  В2. Найдите наибольшее целое решение неравенства (log_0,3 (x + 1)) / (log_0,3 100 – log_0,3 9) < 1.
  
• 
  ВЗ. Вычислите (⁶√7 – ⁶√2)(⁶√7 + ⁶√2)((³√7 + ³√2)² – ³√14).
  
• 
  В4. Сколько корней уравнения sin х + cos х = √2 принадлежит отрезку [–π; 2π]?
  
• 
  В5. На соревнованиях по кольцевой трассе первый лыжник проходил круг на 2 мин быстрее второго и через час обогнал его на целый круг. За сколько минут первый лыжник проходил один круг?
  
• 
  В6. Вычислите sin (π/6 + a), если sin а = √3/2 и 0 < а < π/2.
  
• 
  В7. Найдите значение выражения (1 + cos 2а – sin 2а) / (cos а + cos (π/2 + a)), если cos a = –1/2.
  

---

Алгебра 10 класс (Никольский)
Итоговый тест. Вариант 2

К-8. Вариант 2 (транскрипт)

ЧАСТЬ I. К каждому из заданий А1–А13 дано 4 ответа, из которых только один верный. Для каждого задания запишите номер выбранного вами правильного ответа.

• 
  А1. Упростите выражение ³√b : b^–1/6.
  
• 
  A2. Упростите выражение (a^2/3 – 4)/(a^1/3 – 2) – a^1/3.
  
• 
  АЗ. Упростите выражение log₄ 48 – log₄ 3 + 6^{log6 5}.
  
• 
  A4. Решите неравенство (1/3)^x–3 < 1/9.
  
• 
  А5. Укажите промежуток возрастания функции у = f(x), заданной графиком (рис. 43).
  
• 
  А6. Упростите выражение 2 sin² a/2 + cos а – 1.
  
• 
  А7. Решите уравнение log₅ х = –1.
  
• 
  А8. Укажите промежуток, которому принадлежит корень уравнения log₃(x + 1) = 2.
  
• 
  А9. Найдите область определения функции у = √((x + 1)/(x – 1)).
  
• 
  А10. Решите неравенство 4^х ≥ 8.
  
• 
  А11. Решите неравенство 3^х+2 – 3х < 24.
  
• 
  А12. Найдите произведение корней уравнения lg² x + lg x – 12 = 0.
  
• 
  А13. Решите уравнение 2 sin² x – 3 cos x = 0.
  

ЧАСТЬ II. К каждому из заданий В1–В7 укажите полученный вами ответ (только число).

• 
  В1. Найдите сумму корней уравнения 1/(5 • 2^x – 9) = 1/(4^x – 5).
  
• 
  В2. Найдите наибольшее целое решение неравенства (log_0,2(x + 1,5)) / (log_0,2 100 – log_0,2 4) < 1.
  
• 
  ВЗ. Вычислите ((³√5 – ³√2)² + 4³√10)((³√5 – ³√2)² + ³√10).
  
• 
  В4. Сколько корней уравнения sin х – cos х = –√2 принадлежит отрезку [–2π; 2π]?
  
• 
  В5. На соревнованиях по кольцевой трассе первый велосипедист проходил круг на 5 мин медленнее второго и через час отстал от него на целый круг. За сколько минут второй велосипедист проходил один круг?
  
• 
  В6. Вычислите cos (π/3 + a), если sin a = 1/2 и 0 < a < π/2.
  
• 
  В7. Найдите значение выражения (1 – cos 2a + sin 2a) / (cos a – sin (2π – a), если sin a = –1/2.
  

 

Ответы на итоговый тест



 

---

Смотрите также файлы

• Отчет по учебной практике Проверил Дата защиты.docx

• Контрольная работа дисциплина Корпоративные финансы Ф. И. О студента Гукин Иван Алексеевич.docx

• Предпринимательство, предприимчивость и риск.docx

• Алканы.pptx

• Сравнение структуры и свойств водородных соединений s и рэлементов i и iv групп.docx