Практическое занятие 2

 Задание 1.

Таблица – «Виды моделирования при решении текстовых задач»
В таблице «Виды моделирования при решении текстовых задач» заполните позицию «Необходимо определить» в графе «Интерпретация модели».

Задача	Модель	Интерпретация модели
1.     1. Было 7 кубиков, проиграно 4 кубика. Сколько кубиков осталось?		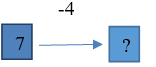Пример ответа: Известно: начальное состояние объекта; направленность отношения между начальным и конечным состоянием объекта; числовое значение величины отношения между состояниями объекта. Необходимо определить числовое значение величины конечного состояния объекта.
2. Было 4 кубика, стало 7 кубиков. Что произошло?		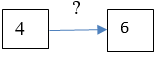Известно: начальное и конечное состояние объекта; направленность отношения между ними. Необходимо определить.... Числовое значение конечного объекта.
3. Имеется 7 кубиков после того, как добавили 4 кубика. Сколько кубиков было до добавления?		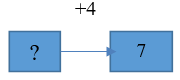Известно: значение величины конечного состояния объекта, направленность отношений между состояниями объекта и числовое значение величины отношений между состояниями объектов. Необходимо определить ... Числовое значение величины начального состояния объекта.
4.Было 7 кубиков, стало 4 кубика. Что произошло?		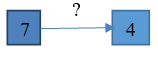Известно: значение величины начального и конечного состояния объекта, направленность отношений между состояниями объекта. Необходимо определить ... Числовое значение конечного объекта.
5.В первый раз принесли 7 кубиков, во второй раз – забрали 4 кубика. Что произошло в результате?		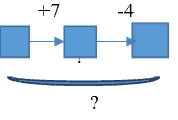Известно: направленность отношений между состояниями объекта; числовое значение величин отношений между состояниями объекта (начального, промежуточного и конечного). Необходимо определить ... Значение величины отношения между начальным и конечным состояниями.
6. В первый раз забрали 7 кубиков, во второй – принесли 4 кубика. Что произошло в результате?		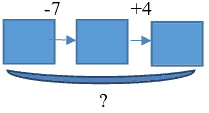Известно: направленность отношений между состояниями объекта; числовое значение величин отношений между состояниями объекта. Необходимо определить ... Значение величины отношения между начальным и конечным состояниями.
7.В первый раз забрали 4 кубика. После того, как кубики забрали второй раз, всего было отдано 7 кубиков. Что произошло во второй раз?		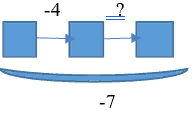Известно: направленность отношений между состояниями объекта; числовое значение величин отношений между состояниями объекта. Необходимо определить ...Значение величины отношения между начальным и конечным состояниями.
8. В первый раз забрали 7 кубиков. После того, как во второй раз принесли кубики, оказалось, что всего было отдано 4 кубика. Что произошло во второй раз?		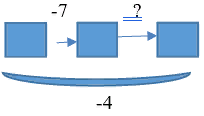Известно: направленность отношений между состояниями объекта; значение величин отношений между начальным и промежуточным, между промежуточным и конечным состоянием объекта. Необходимо определить ... Значение величины отношения между начальным и конечным состояниями.

---

 

Задание 2.
 Используя диаграммы Эйлера-Венна решить задачу.

При выборе кружков для детей оказалось, что 60% родителей желают, чтобы их ребенок посещал кружок рисования, 50% предпочли занятия по гимнастике, 50% отметили, что выбрали бы занятия музыкой. При этом 30% родителей предпочитают, чтобы их дети посещали занятия и по рисованию, и по гимнастике,  20% – сделали выбор в пользу занятий по гимнастике и музыке,  а 40% родителей –  пожелали бы, чтобы ребенок рисовал и занимался хоровым пением, и только 10% из них выразили свое мнение за посещение детьми всех кружков. Определите процентное соотношение родителей, которые:

1) не желают водить детей в кружки;

2) выбрали не менее двух кружков.

 1) не желают водить детей в кружки – 30% родителей

2) выбрали не менее двух кружков – (30-10)+(20-10)+(40-10)+10=70 (%)

Задание 3
При измерении получены данные:

Номер измерения	1	2	3	4	5	6	7	8	9	10
Данные	20	20	5	10	10	15	20	5	5	20

Выполните задания с учетом исходных данных, подробно описывая ход решения.

a)           Построить статистический ряд распределения частот.

b)          Построить полигон распределения.

c)           Вычислить выборочную среднюю, дисперсию, моду, медиану.

d)          Построить выборочную функцию распределения.

 

Задание 4 (максимальное количество баллов - 4 балла)

---

 

Решите примеры, связанные с погрешностями, подробно описывая ход решения.

a)   Округлить число 4,45575250 до шести, пяти, четырех, трех, двух и одного десятичных знаков; до целого числа.

b)   Число 12,75  определено  с относительной погрешностью 0,3, %. Найдите абсолютную погрешность округления.

c)   Определите верные и сомнительные цифры числа 13,27 ± 0,03.

a) 4,45575250 до шести знаков = 4,455753
4,45575250 до пяти знаков = 4,45575
4,45575250 до четырёх знаков = 4,4558
4,45575250 до трех знаков = 4,456
4,45575250 до двух знаков = 4,46
4,45575250 до одного знака = 4,5
4,45575250 до целого числа = 4

b) Округляя число 12,75 получаем 12,8. Прибавляем 1 к десятым, потому что сотые больше 5.
Абсолютная погрешность равна модулю разницы между точным и округленным числом, 12,8 – 12,75 = 0,05
Относительная погрешность равна абсолютной, деленной на приближенное значение, выраженное в процентах, 0,05 / 12,8 * 100% = 0,003%

c) Определение: «Цифра называется верной, если граница абсолютной погрешности данного приближенного значения числа не больше единицы того разряда, в котором записана эта цифра. В противном случае цифра называется сомнительной».
х = 13,75 ± 0,03
0,03 - граница абсолютной погрешности
Единица последнего разряда - 0,01 (сотые)
0,03 > 0,01
значит цифра 5 - сомнительная
0,03 < 0, 1 - значит цифра 2 - верная
Если в записи приближенного значения числа какая-то цифра – верная, то и все предшествующие ей цифры так же являются верными.
Значит 3; 1 - также верные цифры
В записи приближенного  значения числа сохраняют только верные цифры, а сомнительные цифры округляют, значит
х = 13,3

 

Задание 5 (максимальное количество баллов – 3 балла)

 

Решите задачу, подробно описывая ход рассуждений. Решение сопроводите графическим отображением.

На стороне AC треугольника ABC отмечена точка D так, что AD=3см, DC=10см. Площадь треугольника ABC равна 39 см². Найдите площадь треугольника ABD.

Дано: треугольник ABC, AD=3см, DC=10см, S треугольника ABC=39 см².
Найти: S треугольника ABD
Решение:

---

BH – общая высота, следовательно SABC/SABD = AC/AD
39/SABD = 13/3

13 SABD = 39*3
SABD = 39*3/13 = 9
Ответ: 9 см².

 

Задание 6 (максимальное количество баллов – 4 балла)

 

Решите задачу, подробно описывая ход рассуждений. Решение сопроводите графическим отображением.

Биссектриса угла A параллелограмма ABCD пересекает его сторону BC в точке F. Найдите площадь параллелограмма ABCD, если BF=4 см, FC=2 см, а угол ABC равен 150⁰.

 Дано: параллелограмм ABCD, BF=4 см, FC=2 см, ∠ABC=150⁰.
Найти: S параллелограмма ABCD
Решение: Накрест лежащие углы BFA и FAD равны, AF — биссектриса ∠BAD, следовательно, ∠ BFA и ∠ FAD = ∠ BAF
Значит, треугольник BFA равнобедренный и  AB=BF=4
По формуле площади параллелограмма находим:


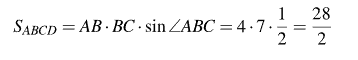
Ответ: 14

Задание 7 (максимальное количество баллов – 3 балла)

 

Решите задачу, подробно описывая ход рассуждений. Решение сопроводите графическим отображением.

Найдите площадь поверхности прямой призмы, в основании которой лежит ромб с диагоналями, равными 6см и 8см, а боковое ребро призмы равно 12см.

Сторона ромба a выражается через его диагонали    и    формулой

   

Найдем площадь ромба

   

---

Тогда площадь поверхности призмы равна   

     
Ответ: 288

 

Примечание

Приведем вывод используемой в решении формулы, выражающей сторону ромба a через его диагонали d₁ и d₂. Диагонали ромба перпендикулярны и точкой пересечения делятся пополам, следовательно, по теореме Пифагора

---

Смотрите также файлы

• Вопросы Каково содержание правоспособности граждан.docx

• ЖасДарын3 бастауыш мектебі.docx

• Отчет по ознакомительной практике обучающийся гр. Фпмц20 Саранская А. А. 05. 02. 2021 г. 02. 06. 2021 г.docx

• I вариант Найдите координаты середины отрезка ав, если а (34) и в (12). Даны точки а (42) и В(12). Найдите расстояние между этими точками..docx

• Старкова Татьяна Андреевна Задание 1 Кобзева Я. А федеральный государственный образовательный стандарт.doc