На следующем этапе привлекается широкий коллектив экспертов, который разбивается на относительно небольшие подгруппы для оценки каждой из целей S₁, S₂,...,S_m+n. Каждому из экспертов, оценивающему цель S_iпосылается анкета с формулировкой этой цели и списком всех ее предварительных предпосылок. Из этого списка эксперт должен выбрать те цели, достижение которых он считает непременным условием для достижения цели S_i(i= 1,2, . . . ,m+n), и дополнить его недостающими на его взгляд целями.

Назовем совокупность всех промежуточных целей, выставленных экспертом j для цели i, предпосылкой ij.

Эксперт оценивает время, необходимое для достижения цели S_iпри условии, что все цели предпосылки ij уже достигнуты. Эта оценка (обозначим ее через t_ij), как и в методе Дельфы, предполагает возможность бесконечного значения, т. е. цель никогда не может быть достигнута. Разумеется, в этом случае предпосылка ijпредполагается пустой. Кроме того, эксперт дает качественную оценку своей компетентности (применительно к данной цели) и степени уверенности в своем прогнозе. Эти оценки переводятся в весовые коэффициенты β_ij и γ_ij, произведение которых β_ij - γ_ij = δ_ijпредставляет собой вес данного единичного прогноза.

Эксперту предлагается также назвать фамилии нескольких специалистов, которых он считает целесообразным привлечь для прогноза по событию S_i (i=1,2,...,m+n). Те эксперты, фамилии которых были указаны их коллегами, получают добавку Δβ_ij к самооценке своей собственной компетентности β_ij тем большую, чем чаще упоминались их фамилии. Теперь необходимо для каждой цели S_i определить предпосылки с набором оценок. В общем это должно выполняться периодически (например, один раз в полтора года).

Заполненные анкеты обрабатываются, строится граф соподчиненности целей. Для любого эксперта j, оценивавшего цель S_i, все цели предпосылки ijсоединяются стрелками с целью S_iаналогично тому, как было описано.

Построенный граф проверяется на отсутствие циклов. Если в нем оказываются петли

---

, то их устраняют, проведя дополнительную работу с экспертами (хотя в ряде случаев можно работать и с неустранёнными петлями). Так в конце концов получается прогнозный граф.
Систематизируя полученный в результате проведения экспертизы массив исходных данных, выявляют адекватные условия, объединяют некоторые условия в одно, а также искусственно заземляют часть условий в графе, после чего начальные данные и связи в графе кодируются для машинной обработки.

Анализ прогнозного графа включает в себя:

1) поиск циклов и тупиковых событий в прогнозном графе;

2) ранжирование событий в прогнозном графе;

3) вычисление вероятностных и временных характеристик;

4) варьирование вероятностных и временных характеристик.

События в прогнозном графе (т. е. вершины его, соединенные дугами) — это проблемы (исходные и промежуточные цели) и эксперты.

Граф должен удовлетворять следующим условиям:

- в нем не должно быть событий, из которых не выходит ни одной связи, если только эти события не завершающие (имеющие пустые предпосылки ij);

- в нем не должно быть событий, в которые не входит ни одной связи, если только эти события не исходные цели (проблемы);

- в нем не должно быть замкнутых контуров, т. е. не должно быть связей, соединяющих какое-либо событие с ним же самим;

- в нем не должно быть событий, имеющих одинаковые шифры. Поэтому первое, что следует сделать при анализе графа, — выявить все ошибки, допущенные при его составлении.

Рассмотрим порядок поиска тупиковых событий и циклов. Событие, в которое не входит ни одна работа и которое не является исходным событием для данного графа, называется тупиковым событием первого рода. Событие же, из которого не выходит ни одна работа и которое не является конечным для данного графа, является тупиковым событием второго рода.

Исходная информация формируется в виде некоторого массива (событие и связи — работы), затем путем последовательного выбора кодов связи и выделения из них кодов начальных событий создается новый массив, содержащий начальные события с признаками работ, исходящих из этих событий. Наконец, выделяются конечные события, их включают в сформированный массив с признаками работ, входящих в данные события.

После пересмотра всех связей-работ входной информации сформированный массив будет включать все события графа с соответствующими признаками входящих и исходящих связей. При этом признаки тупиковых событий первого и второго рода примут, например, соответственно следующий вид: 01 и 10. Признаком кодов всех нетупиковых условий будет в этом случае сочетание 11. В результате просмотра признаков всех событий, записанных в сформированный массив, выявятся тупиковые события первого и второго рода.

---

Согласно данному алгоритму начальные и конечные события графа снабжены соответствующими признаками.

Допустим, имеется прогнозный граф с М вершинами и Nдугами. На вершинах m=l,2,... , М данного графа определяется функция
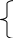1, если вершина принадлежит контуру или пути, начинающемуся

φ(m)= на контуре;

0, в противном случае.
Вычисляют φ(m) рекуррентным образом при пoмощи последовательности

Вспомогательных функций ψ_k(m) ≤ ψ_k-1,m=1,2,…,Mсходящейся к φ(m): ψ_k0(m)≡ ψ_k0(m)≡ φ(m) при некотором конечном k₀. Строится функция ψ_k(m) следующим образом.

Положим ψ₀(m) ≡ 1, a ψ_k-1(m) вычислена. Вычисляем ψ_k(m) следующим образом: последовательно просматриваем список дуг (i, j), i и j— начало и конец дуги. Если ψ_k-1(i) = 0, то переходим к следующей дуге. В противном случае если ψ_k-1(i)=1, то ψ_k(j)=1. Всем ψ_k(m), не определенным после полного просмотра списка дуг, приписывают значение 0.

Рассмотрим геометрический смысл этого рекуррентного построения. Первоначально значение ψ₁(m) = l получает каждая вершина, в которую входит хотя бы одна дуга. Следовательно, ψ₁(m) = 0 на тех вершинах, куда не входит ни одна дуга. Эти вершины исключаются из дальнейшего рассмотрения, так как они не могут лежать на контуре или на пути, выходящем из контура.

Граф сокращается за счет исключения дуг, выходящих из начальных вершин (т. е. вершин, не имеющих входящих в них дуг). Но в нем появляются новые начальные вершины, поскольку из графа исключаются все незамкнутые пути, выходящие из начальных вершин (т. е. мы подойдем к контуру, если он имеется в графе).

Если φ(m)=0 (т=1, 2,...,М),то контуров в графе нет. Если же φ(m)≠0, то граф содержит контуры. В этом случае строится функция:

---

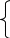
1, если вершина принадлежит контуру или пути, начинающемуся

φ*(m) = на контуре;

0, в противном случае.

Чтобы вычислить функции φ*_k, нужно построить последовательность по дугам с обратной ориентацией точно так же, как последовательность ψ_k.

Вершины, в которых ф(т)=ф*(т)=*1, принадлежат одному из контуров.

Рассмотрим порядок ранжирования событий в графе с целью преобразования исходной информации к виду, удобному для вычисления временных и вероятностных характеристик. Используем для этого одну из модификаций стандартных способов ранжирования событий, применяемых в сетевом планировании.

Множество событий в графе разбивается на слои, начиная с уровня событий, не имеющих предпосылок i,j (так называемая «земля» — события класса ko). Событие S_iпринадлежит уровню ρ, если все его предпосылки принадлежат меньшим уровням и хотя бы одна — в точности уровню ρ — 1 (ρ = 1, 2, . . . , q, . . . ), начиная с «заземленного уровня» (класс k₀), q — число уровней в графе).
Вычисление временных характеристик производят по следующей формуле:



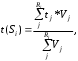
г де t(S_i) — время свершения события S, графа;

t_j — время свершения события S_i согласно варианту эксперта j (j=l, 2, . . ., R_i);

V_j — вес эксперта j;

R_i — количество экспертов, оценивающих событие S_i в графе (i= 1, 2, . . . , т+п).

Временные характеристики для каждого варианта (эксперта j) определяются так:

t_j(S_i) =max t(S_ir)+t_ij ,

где t_j(S_i) — время реализации проблемы S_i согласно варианту эксперта j;

t (S_ir) — время свершения выдвинутых экспертом j условий S_irj предпосылке;

t_ij — условное время, заданное экспертом;

S_ir — событие, входящее в предпосылку i,jцели Si (r =l, 2,..., nj).

Аналогично (с незначительными изменениями) вычисляются и стоимостные характеристики.

Вероятностные характеристики рассчитывают следующим образом.

1. Вероятность свершения условий, выдвинутых Эj экспертом при наличии значения абсолютных вероятностей событий «заземленного уровня» (пустые

---

ij — предпосылки):

Pэj (S_ir) =P(S_i1 Λ S_i2 Λ … Λ S_inj)=p_i1 · p_i2 ·… ·p_inj ,

где p_i1 , p_i2 ,… ,p_inj — абсолютные вероятности свершения отдельных условий, выдвинутых экспертом j;

n_ij — количество условий, выдвинутых j-м экспертом; Pэj (S_ir) — вероятность выполнения ijпредпосылки.

2. Pэj (S_ir) — вероятность свершения события S_iанализируемого экспертом jпри предпосылке ij;

pij — условная вероятность, выставленная Эjэкспертом:

pэj (S_i)= pэj (S_ir) pij .

3. Для всех пар экспертов определяются условные вероятности:



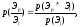
где p(Эp/Эl) вычисляется по общим формулам теории вероятностей. Например:

Si=(Э₁ (S₂ , S₃ , S₄) , Э₂ (S₃ , S₄, S₅) ) ;

p (Э₁ ΛЭ₂) =p ( (S₂ Λ S₃ Λ S₄) Λ (S₃ Λ S₄ Λ S₅) ) = p(S₂Λ S₃ Λ S₄Λ S₅) =

= p₂ ·p₃ ·p₄ ·p₅;



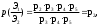
Если для какой-либо пары экспертов p(Э_р / Э_l) или р(Э_l/Э_р) ≥0,5, то производится усреднение вероятностей по формуле:

V _{р l} = min(V_р, V_l)



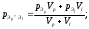
(p, l = 1, 2, … ,k).

После этого присваивается

p (Э_p), еслиp(Эp/Эl) р(Э_l/Э_р) ;

p(Э_р Э_l) =

p(Э_l) в противном случае.

Заметим , что усреднение начинается с тех пар экспертов , которые имеют максимальное значение условных взаимных вероятностей (среди равнозначных порядок безразличен).

Значение p _{Э р}V_{Э l}и V_pV_l

---

Смотрите также файлы

• Календарнотематическое планирование киноуроков на 20222023 учебный год месяц Тема класс ответственный сентябрь Киноурок Мандарин (понятие радость за другого).docx

• Институт строительства и архитектуры Направление строительство зданий, сооружений и развитие территорий Внутренняя политика Александра 3.docx

• Использование методики кластерной оценки для оптимизации образовательного процесса в моу сош 37.docx

• Превращение и сохранение энергии.docx

• Федор Емельяненкою. Достижение.docx