Контрольная работа за 2 семестр

2 вариант

1. N одинаковых источников ЭДС с одинаковым внутренним сопротивлением r=1 Ом соединяют в батарею и подключают к клеммам этой батареи нагрузку с сопротивлением R=5 Ом. Если все источники ЭДС соединены в батарею последовательно, то на нагрузке выделяется в 9 раз большая мощность, чем в том случае, когда батарея собрана из параллельно соединенных источников. Найти число N источников ЭДС.



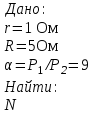
Решение

Если источники соединены последовательно:

сопротивление батареи:

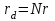(1)

ЭДС батареи:

(2)

где ЭДС одного источника.

Мощность, выделяемая на нагрузке:

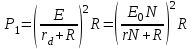(3)

Если источники соединены параллельно:

сопротивление батареи:

(4)

ЭДС батареи:

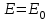(5)

где ЭДС одного источника.

Мощность, выделяемая на нагрузке:

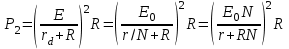(6)

Тогда:

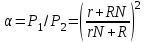(7)

Из (7) получаем:

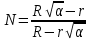(8)

Числовое значение:



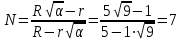
Ответ: .

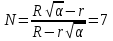2. Материальная точка движется вдоль оси х так, что ее скорость зависит от координаты х по закону v = (A - Bx² )^{1/ 2} , где A = 136м²/с², В = 100с² . Показать, что уравнение движения точки является динамическим уравнением гармонических колебаний и найти период Т этих колебаний.



Решение

Материальная точка движется вдоль оси х так

---

, что ее скорость зависит от координаты х по закону

v = (A - Bx² )^{1/ 2} (1)

Найдем закон изменения ускорения:

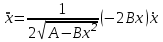(2)

Подставим (1) в (2):

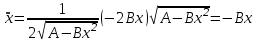(3)

Тогда дифференциальное уравнение примет вид:

(4)

Частота колебания:

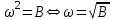(5)

Период колебания:

(6)

Числовое значение:



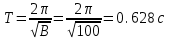
Ответ: .

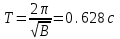3. Энтропия некоторой термодинамической системы изменяется с температурой Т по закону S = bT⁵ +const , где b = 2∙10^-10 Дж/ К⁶ . Определить теплоемкость C этой системы при температуре T = 200 К.



Решение

Энтропия некоторой термодинамической системы изменяется с температурой Т по закону

S = bT⁵ +const (1)

С другой стороны:

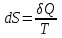(2)

Тогда

(3)

Следовательно:



Числовое значение:



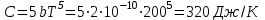
Ответ: .

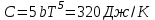4. Бесконечный тонкий прямой проводник равномерно заряжен с линейной плотностью заряда λ = 5∙10^-10 Кл / м. Считая, что на расстоянии r₁ =1м от проводника потенциал созданного им электрического поля равен 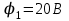, определить величину потенциала на расстоянии r₂= e= 2,72м от проводника .



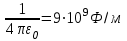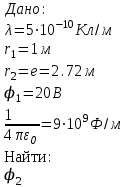
Решение

Ограничим пространство вокруг проводника цилиндрической поверхностью, ось симметрии которой совпадает с проводником. Используем теорему Гаусса:

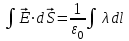(1)

---

Тогда:

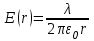(2)

Найдем потенциал:

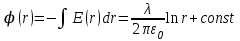(3)

Следовательно:

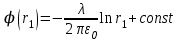(4)

(5)

Из (4) и (5) находим:

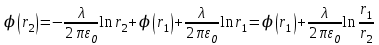(6)

Числовое значение:



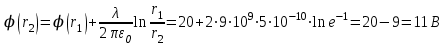
Ответ: .

5. Сколько главных максимумов будет видно за дифракционной решеткой, изготовленной нанесением N=3000 равноудаленных штрихов на прозрачную полоску длины L=1см? Свет с длиной волны 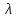= 600нм падает на решетку нормально.



Решение

Уравнение дифракционной решетки:

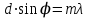(1)

Условие нахождения максимального порядка максимума:

(2)

Период решетки:

(3)

Из (2) и (3) получим:

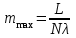(4)

Числовое значение:



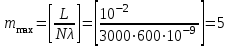
Ответ: .

---

Смотрите также файлы

• Практикум по наблюдению и наблюдательности е изд, переработанное и дополненное. Спб. Питер, 2008. 208 сил (Серия Практикум по психологии ).pdf

• Бухгалтерский учет на предприятиях малого бизнеса организация и порядок ведения, особенности правового регулирования.pdf

• Сочинение Проблема жизненного пути.docx

• Министерство науки и высшего образования российской федерации обнинский институт атомной энергетики.docx

• 1 производственноэкономическая характеристика хозяйства 1 Общие сведения о предприятии.docx