Теперь мы можем закодировать исходную фразу.

000 1010 11110 11111 001 01001 1001 000 1011 1000 0100 1010 01011 0110 001 0100 11000 01010 11010 1000 0111 11100 001 11011 0100 11101 11001 1001 000 1011

Ответ: 000 1010 11110 11111 001 01001 1001 000 1011 1000 0100 1010 01011 0110 001 0100 11000 01010 11010 1000 0111 11100 001 11011 0100 11101 11001 1001 000 1011.

7. На любой из позиций двоичного кода может быть с равной вероятностью переданы «0» и «1». Помехи преобразуют «1» в «0» с вероятностью 0,02 и «0» в «1» с вероятностью 0,04. Найти вероятность того, что был передан «1», если принят «1».

Событие B1 - был передан ноль, событие B2 - была передана единица. Эти события несовместны и образуют полную группу. По теореме сложения вероятностей если два события несовместны, то вероятность наступления каждого из них равна сумме их вероятностей̆

P (X + Y) = P(X) + P(Y) – теорема сложения вероятностей.

Значит P(B1) +P(B2) =1.

Они имеют одинаковую вероятность, так как исхода всего 2, значит

P (B1) = ½=0,5, P(B2) = ½=0,5.

Гипотеза A - принята «1». Оно возможно только при условии, что исполнилось либо событие В1 – был передан «0», либо событие В2 – была передана «1».

Нам благоприятствуют 2 исхода – была передана «1» и принята «1» (помехи не преобразовали «1» в «0»), и был передан «0» и принята «1» (помехи преобразовали «0» в «1»).

События А/В1 – была принята «1» при переданном нуле и не А/В1 – был принят «0» при переданном «0» – противоположны, сумма вероятностей противоположных событий равна «1». Поэтому P(А/В1) + Р (не А/В1) =1.

P(А/В1) =1-Р (не А/В1) =1- 0,04= 0,96 - «1» принята при переданной «1».

P(А/B2) = 0,02 - «1» принята при переданном нуле.

Теорема. Вероятность полного события, которое может произойти при осуществлении одного из несовместных событий, образующих полную группу, определяется формулой̆:

P(X) = P(Y1)P(X /Y1) + P(Y2)P(X /Y2) + . . . + P(Yn)P(X /Yn) = 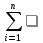P(Yi )P(X /Yi )

Вероятность приема единицы по формуле полной вероятности, записанной выше

P(A)= P(B1) *P(А/B1) + P(B2) *P(А/B2) = 0,5*0,96+ 0,5*0,02= 0,49.

Вероятность А/В2 приёма «1», если передана «1» (то есть помехи не преобразовали «1» в «0») составляет с вероятностью не А/В2 приёма «0», если передана «1» (то есть помехи преобразовали «1» в «0») полную группу. Значит Р(А/В2)- Р (не А/В2) =1,

---

Р(А/В2) =1-0,02=0,98.

В случае, если событие, появляющееся совместно с каким-либо из
несовместных событий, образующих полную группу, произошло и
требуется произвести оценку вероятностей событий , применяется
формула Байеса:



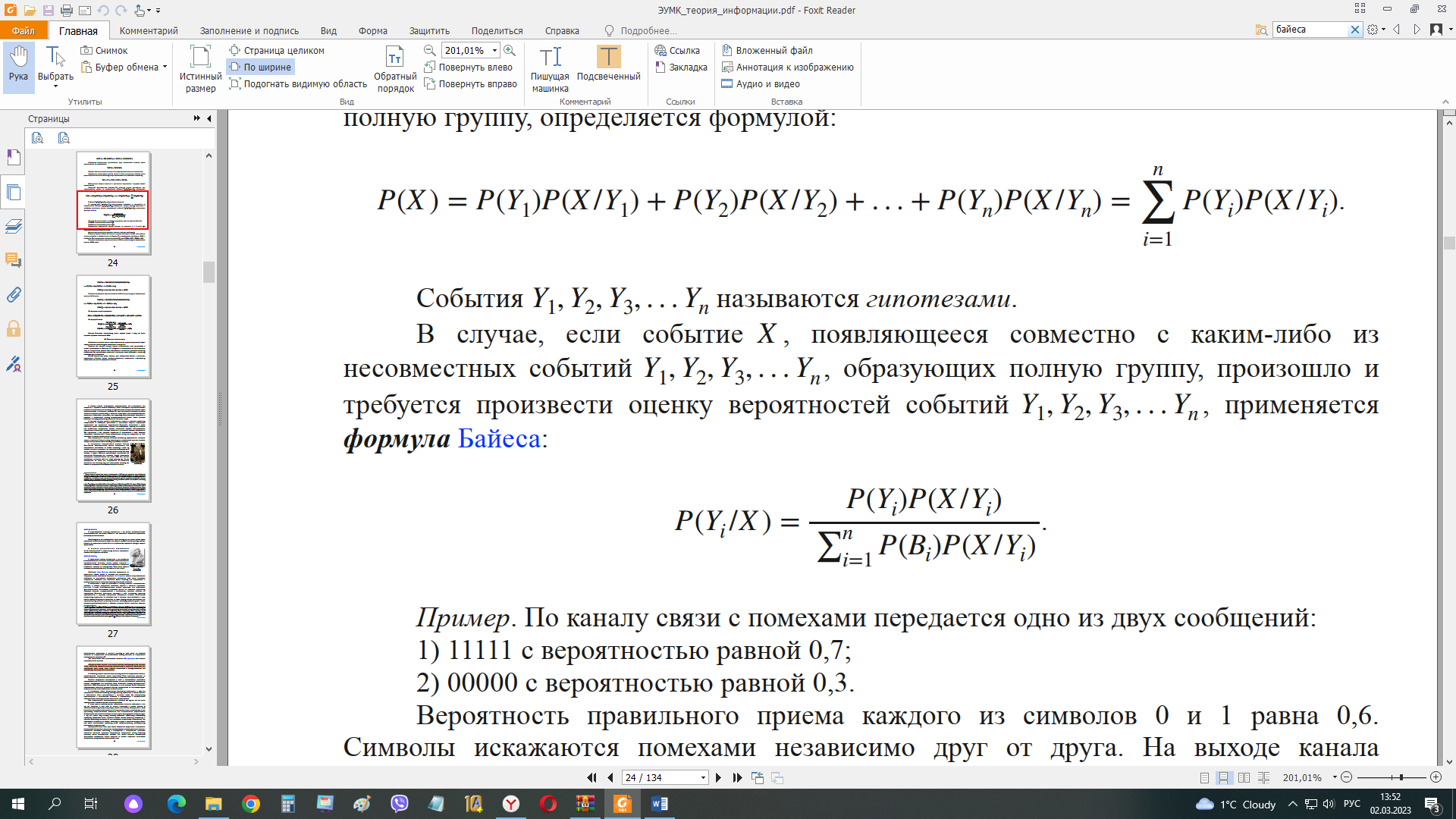
Теорема Байеса для нашего случая

P(A|B2) = P(B2|A) * P(A)/P(B2)

• 
  P(A|B2) – вероятность наступления события А, при условии, что событие В2 уже случилось (принята единица при переданной единице);
  
• 
  P(B2|A) – вероятность наступления события В2, при условии, что событие А уже случилось (Передана единица, если принята единица).
  
• 
  P(A) –вероятность наступления события А (принята 1);
  
• 
  P(B1) –вероятность наступления события В2 (передана 1).
  

Тогда

P(B2|A) =P(A|B2) /P(A)*P(B2) =0,98/0,96*0,5=0,51

Ответ: вероятность того, что был передан «1», если принят «1» равна 0,51.

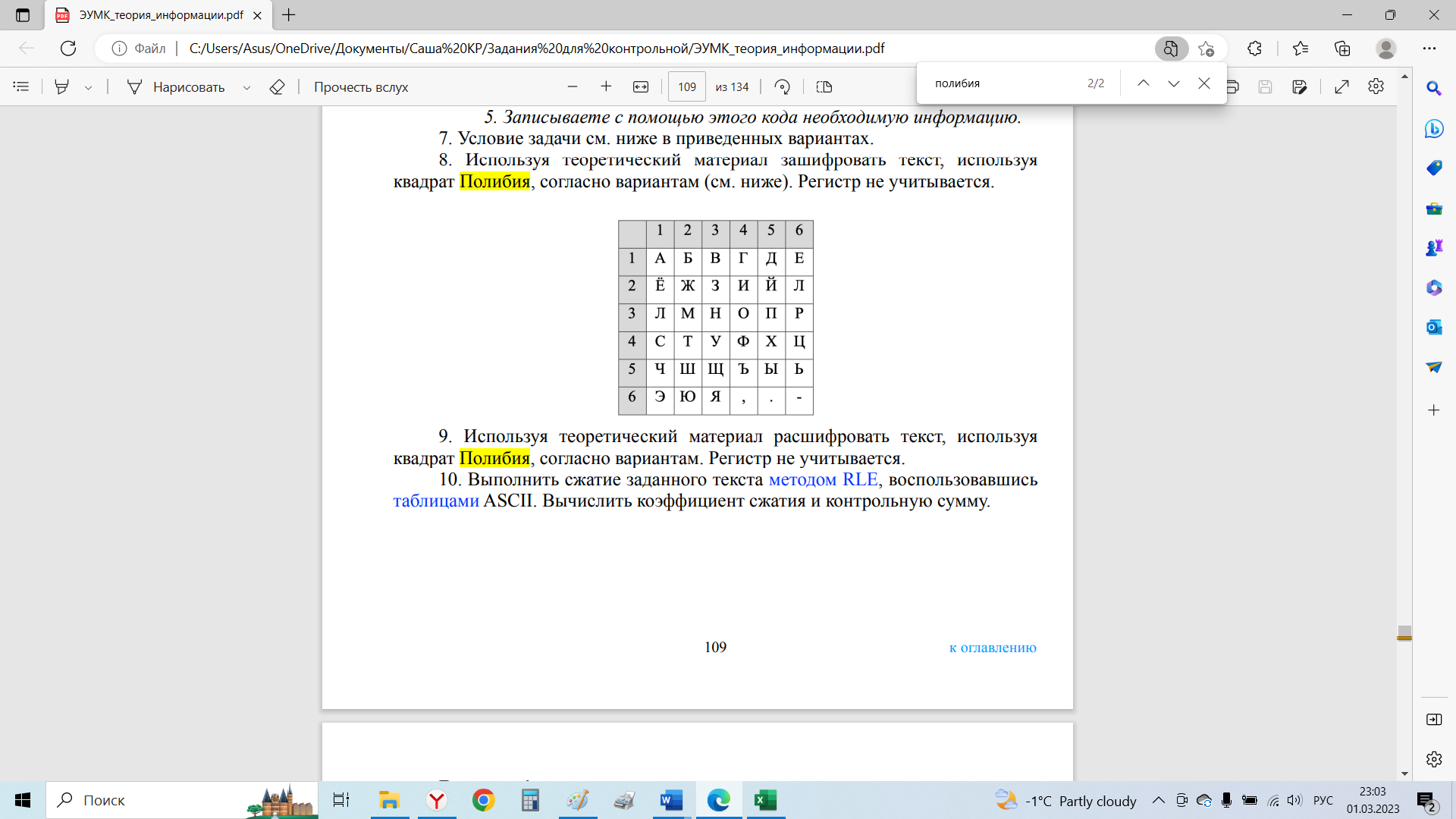
8. Используя теоретический материал зашифровать текст, используя
квадрат Полибия, согласно вариантам (см. ниже). Регистр не учитывается.
Красота до вечера, а доброта навек.



Решение.

Шифрование с помощью квадрата Полибия производится следующим образом – каждой букве ставится в соответствие двузначное число, состоящее из номера строки и номера столбца. Так буква «К» шифруется числом 26, «Р» - 36 и т. д. Для удобства составим таблицу.

Символ	К	р	а	с	о	т	а		д
Код	26	36	11	41	34	42	11		15
Символ	о		в	е	ч	е	р	а	,
Код	34		13	16	35	34	36	11	64
Символ		а		д	о	б	р	о	т
Код		11		15	34	12	36	34	42
Символ	а		н	а	в	е	к	.
Код	11		33	11	13	16	26	65

---

Выпишем коды в строку

26 36 11 41 34 42 11 15 34 13 16 35 34 36 11 64 11 15 34 12 36 34 42 11 33 11 1316 26 65

---

Ответ: 26 36 11 41 34 42 11 15 34 13 16 35 34 36 11 64 11 15 34 12 36 34 42 11 33 11 1316 26 65

9. Используя теоретический материал расшифровать текст, используя
квадрат Полибия, согласно вариантам. Регистр не учитывается.
14 36 63 23 33 43 42 56


Решение.

Расшифруем сообщение, считая 1 цифру номером строки в таблице, а 2 – номером столбца.

14	36	63	23	33	43	42	56
Г	Р	Я	З	Н	У	Т	Ь

Ответ: ГРЯЗНУТЬ

10. Выполнить сжатие заданного текста методом RLE, воспользовавшись таблицами ASCII. Вычислить коэффициент сжатия и контрольную сумму. POIFFFFRdsaRR

Решение.

Из таблиц ASCII выпишем двоичные коды каждого символа, встречающегося в сообщении.

	Символ	Двоичный код	Шаг	Архив
	P	01010000
	O	01001111
	I	01001001
	F	01000110
	F	01000110
	F	01000110
	F	01000110
	R	01010010
	d	01100100
	s	01110011
	a	01100001
	R	01010010
	R	01010010

---

Текст содержит 13 символов, каждый символ кодируется 1 байтом, значит информационный объём текста равен 13 байтам.

Запишем двоичный код нашего сообщения.

01010000 01001111 01001001 01000110 01000110 01000110 01000110 01010010 01100100 01110011 01100001 01010010 01000110.

Упакованные RLE данные состоят из управляющих байтов, за которыми следуют байты данных. Каждый байт состоит из 8 битов (цифр 0 или 1). Старшим считается первый бит (первая цифра). Если старший бит управляющего байта равен 0, то следующие байты (в количестве, записанном в семи младших битах управляющего байта) при упаковке не изменялись. Если старший бит равен 1, то следующий байт нужно повторить столько раз, какое число записано в остальных разрядах

Составим управляющие байты, для этого удобнее смотреть на исходный текст.

Первые 3 символа, а значит и их двоичные коды, не повторяются.

Поэтому первый бит будет 0, а в остальных семи битах (цифрах) мы запишем количество неповторяющихся символов. Их 3, переведём число 3 в двоичную систему счисления.

3	2
-2	1
1

3₁₀ = 11₂

Поскольку число должно состоять из 7 цифр, дополним его впереди нулями.

Итак, управляющий байт для первых трёх символов 0000001.

Выпишем начало цепочки: 01010000 01001111 01001001.

Дальше идут 4 повторяющихся символа, значит управляющий байт начинается с 1, а число повторений – 4 – переведем в двоичную систему.

4	2
-4	2	2
0	-2	1
	0

---

Смотрите также файлы

• А департамент потребительского рынке областной администрации.docx

• Тема дружбы и любви в произведение Маленький принц А. С. Экзюпери план о чем произведение Маленький принц.docx

• На примере задач рынка недвижимости ответьте на следующие вопросы какие данные, подходящие под определение big data, фиксируютсямогут фиксироваться в исследуемой предметной области.pdf

• Существует одна старинная легенда. В ней рассказывается о великой материнской любви. Был у матери единственный сын. Взял он в жены хоть и красивую, но злую девушку и привел ее в дом жить.docx

• Курс лекций по дисциплине Техническая механика для студентов заочного отделения специальности.pdf