Получилось:0,70999999999998₁₀ = 0,55341217270₈
3. Сложим вместе целую и дробную часть вот так:

472₈ + 0,55341217270₈ = 472.55341217270₈

Ответ: 314,71₁₀=472.55341217270₈.

Для того, чтобы перевести число 314.71 из десятичной системы счисления в шестнадцатеричную, необходимо перевести вначале целую часть, а затем дробную. Таким образом потребуется:

Перевести 314 в шестнадцатеричную систему;

1. 
   Перевести 0,71 в шестнадцатеричную систему.
   

1. Для того, чтобы перевести число 314 из десятичной системы счисления в шестнадцатеричную, необходимо осуществить последовательное деление на 16, до тех пор пока остаток не будет меньше чем 16.

—	314		16
	304	—	19		16
	10=A		16		1
			3

Полученные остатки записываем в обратном порядке, таким образом:

314₁₀=13A₁₆

2. Для перевода десятичной дроби 0,71 в шестнадцатеричную систему, необходимо выполнить последовательное умножение дроби на 16, до тех пор, пока дробная часть не станет равной 0 или пока не будет достигнута заданная точность вычисления. 

	0	71
	,	16
	11=B	36
		16
	5	76
		16
	12=C	16
		16
	2	56
		16
	8	96
		16
	15=F	36
		16
	5	76
		16
	12=C	16
		16
	2	56
		16
	8	95996
		16
	15=F	35938
		16

---

Получилось:0,70999999999998₁₀ = 0,B5C28F5C28F₁₆
3. Сложим вместе целую и дробную часть вот так:

13A₁₆ + 0,B5C28F5C28F₁₆ = 13A.B5C28F5C28F₁₆
Ответ: 314,71₁₀=13A,B5C28F5C28F₁₆.

2. Перевести данное число в десятичную систему счисления.

а) 110010001₂; б) 100100000₂; в) 1110011100,111₂; г) 1010111010,1110111₂;
д) 704,6₈; е) 367,38₁₆.


а) 110010001₂.

Решение:

Для перевода числа 110010001 в десятичную систему воспользуемся формулой:

A_n = a_n-1 ∙ q^n-1 + a_n-2 ∙ q^n-2 + ∙∙∙ + a₀ ∙ q⁰

и таблицами степеней числа 2.



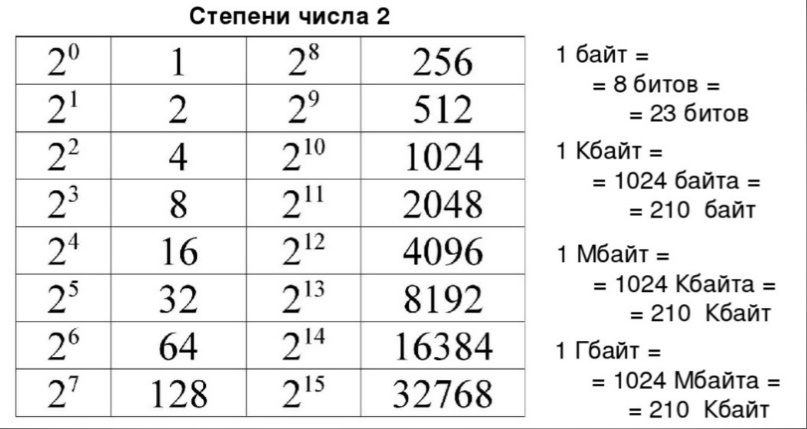
Отсюда:

110010001₂=1 ∙ 2⁸ + 1 ∙ 2⁷ + 0 ∙ 2⁶ + 0 ∙ 2⁵ + 1 ∙ 2⁴ + 0 ∙ 2³ + 0 ∙ 2² + 0 ∙ 2¹ + 1 ∙ 2⁰ = 1 ∙ 256 + 1 ∙ 128 + 0 ∙ 64 + 0 ∙ 32 + 1 ∙ 16 + 0 ∙ 8 + 0 ∙ 4 + 0 ∙ 2 + 1 ∙ 1 = 256 + 128 + 0 + 0 + 16 + 0 + 0 + 0 + 1 = 401₁₀

Ответ: 110010001₂ = 401₁₀.

б) 100100000₂

Для перевода числа 100100000 в десятичную систему воспользуемся формулой:

A_n = a_n-1 ∙ q^n-1 + a_n-2 ∙ q^n-2 + ∙∙∙ + a₀ ∙ q⁰

Отсюда:

100100000₂=1 ∙ 2⁸ + 0 ∙ 2⁷ + 0 ∙ 2⁶ + 1 ∙ 2⁵ + 0 ∙ 2⁴ + 0 ∙ 2³ + 0 ∙ 2² + 0 ∙ 2¹ + 0 ∙ 2⁰ = 1 ∙ 256 + 0 ∙ 128 + 0 ∙ 64 + 1 ∙ 32 + 0 ∙ 16 + 0 ∙ 8 + 0 ∙ 4 + 0 ∙ 2 + 0 ∙ 1 = 256 + 0 + 0 + 32 + 0 + 0 + 0 + 0 + 0 = 288₁₀

Ответ: 100100000₂ = 288₁₀.

в) 1110011100,111₂

Решение:

Для перевода числа 1110011100,111 в десятичную систему воспользуемся формулой:

A_n = a_n-1 ∙ q^n-1 + a_n-2 ∙ q^n-2 + ∙∙∙ + a₀ ∙ q⁰ + a_-1 ∙ q^-1 + ∙∙∙ + a_-m ∙ q^-m

Отсюда:

1110011100,111₂=1 ∙ 2⁹ + 1 ∙ 2⁸ + 1 ∙ 2⁷ + 0 ∙ 2⁶ + 0 ∙ 2⁵ + 1 ∙ 2⁴ + 1 ∙ 2³ + 1 ∙ 2² + 0 ∙ 2¹ + 0 ∙ 2⁰ + 1 ∙ 2^-1 + 1 ∙ 2^-2 + 1 ∙ 2^-3 = 1 ∙ 512 + 1 ∙ 256 + 1 ∙ 128 + 0 ∙ 64 + 0 ∙ 32 + 1 ∙ 16 + 1 ∙ 8 + 1 ∙ 4 + 0 ∙ 2 + 0 ∙ 1 + 1 ∙ 0,5 + 1 ∙ 0,25 + 1 ∙ 0,125 = 512 + 256 + 128 + 0 + 0 + 16 + 8 + 4 + 0 + 0 + 0,5 + 0,25 + 0,125 = 924,875₁₀

Ответ: 1110011100,111₂ = 924,875₁₀.

г) 1010111010,1110111₂

Решение:

Для перевода числа 1010111010,1110111 в десятичную систему воспользуемся формулой:

A_n = a_n-1 ∙ q^n-1 + a_n-2 ∙ q

---

^n-2 + ∙∙∙ + a₀ ∙ q⁰ + a_-1 ∙ q^-1 + ∙∙∙ + a_-m ∙ q^-m

Отсюда:

1010111010,1110111₂=1 ∙ 2⁹ + 0 ∙ 2⁸ + 1 ∙ 2⁷ + 0 ∙ 2⁶ + 1 ∙ 2⁵ + 1 ∙ 2⁴ + 1 ∙ 2³ + 0 ∙ 2² + 1 ∙ 2¹ + 0 ∙ 2⁰ + 1 ∙ 2^-1 + 1 ∙ 2^-2 + 1 ∙ 2^-3 + 0 ∙ 2^-4 + 1 ∙ 2^-5 + 1 ∙ 2^-6 + 1 ∙ 2^-7 = 1 ∙ 512 + 0 ∙ 256 + 1 ∙ 128 + 0 ∙ 64 + 1 ∙ 32 + 1 ∙ 16 + 1 ∙ 8 + 0 ∙ 4 + 1 ∙ 2 + 0 ∙ 1 + 1 ∙ 0,5 + 1 ∙ 0,25 + 1 ∙ 0,125 + 0 ∙ 0,0625 + 1 ∙ 0,03125 + 1 ∙ 0,015625 + 1 ∙ 0,0078125 = 512 + 0 + 128 + 0 + 32 + 16 + 8 + 0 + 2 + 0 + 0,5 + 0,25 + 0,125 + 0 + 0,03125 + 0,015625 + 0,0078125 = 698,9296875₁₀

Ответ: 1010111010,1110111₂ = 698,9296875₁₀.

д) 704,6₈

Решение:

Для перевода числа 704,6 в десятичную систему воспользуемся формулой:

A_n = a_n-1 ∙ q^n-1 + a_n-2 ∙ q^n-2 + ∙∙∙ + a₀ ∙ q⁰ + a_-1 ∙ q^-1 + ∙∙∙ + a_-m ∙ q^-m

Отсюда:

704,6₈=7 ∙ 8² + 0 ∙ 8¹ + 4 ∙ 8⁰ + 6 ∙ 8^-1 = 7 ∙ 64 + 0 ∙ 8 + 4 ∙ 1 + 6 ∙ 0,125 = 448 + 0 + 4 + 0,75 = 452,75₁₀

Ответ: 704,6₈ = 452,75₁₀.

е) 367,38₁₆.

Решение:

Для перевода числа 367,38 в десятичную систему воспользуемся формулой:

A_n = a_n-1 ∙ q^n-1 + a_n-2 ∙ q^n-2 + ∙∙∙ + a₀ ∙ q⁰ + a_-1 ∙ q^-1 + ∙∙∙ + a_-m ∙ q^-m

---

Отсюда:

367,38₁₆=3 ∙ 16² + 6 ∙ 16¹ + 7 ∙ 16⁰ + 3 ∙ 16^-1 + 8 ∙ 16^-2 = 3 ∙ 256 + 6 ∙ 16 + 7 ∙ 1 + 3 ∙ 0,0625 + 8 ∙ 0,00390625 = 768 + 96 + 7 + 0,1875 + 0,03125 = 871,21875₁₀

Ответ: 367,38₁₆ = 871,21875₁₀.

3. Выполните арифметические действия в заданных системах счисления.

3765₈ + 122₈.

Все числа находятся в восьмеричной системе счисления. Поэтому все расчеты будем выполнять в ней.

1) Выполним сложение 3765₈+122₈

В восьмеричной системе счисления 8 цифр – 0,1,2,3,4,5,6,7. Число 8 – это уже восьмеричный «десяток», и записывается он как 10.

Используем таблицу сложения восьмеричных чисел.

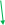
+	3	7	6	5
		1	2	2
	4	1	0	7

5+2=7. Т.к 6+2=10 в восьмеричной системе, пишем 0 и в следующий разряд переносим единицу. 7+1=10, и плюс единица из предыдущего разряда, то есть 11. Опять единица переходит в следующий разряд. И 3+1=4.

---

Получилось: 3765₈+122₈ = 4107₈

Ответ:4107₈

4. Среди приведённых ниже трёх чисел, записанных в различных системах счисления, найдите максимальное и запишите его в ответе в десятичной системе 3216, 608, 1101102.

Решение.

Для удобства сравнения переведём все числа в десятичную систему счисления. Для этого воспользуемся формулой перевода чисел из одной системы счисления в другую.

A_n = a_n-1 ∙ q^n-1 + a_n-2 ∙ q^n-2 + ∙∙∙ + a₀ ∙ q⁰

32₁₆=3*16¹+2*16⁰=3*16+2*1=48+1=49₁₀.

608=6*8¹+0*8⁰=6*8+0*1=48₁₀.

1101102=1*2⁵+1*2⁴+0*2³+1*2²+1*2¹+0*2⁰=1*32+1*16+0*8+1*4+1*2+0*1=32+16+0+4+2+0=54₁₀.

Максимальным из этих чисел будет 1101102.

Ответ: 54₁₀.

5. Юстасу необходимо передать следующее сообщение:
Дорогой Алекс! От всей души поздравляю с успешной сдачей экзамена по
информатике. Желаю дальнейших успехов. Ваш Юстас.
Пеленгатор определяет место передачи, если она длится не менее 3 минут. С какой скоростью (бит/с) Юстас должен передавать радиограмму?
Решение:

Бит — минимальная единица измерения количества информации. Подсчитаем объем передаваемой информации. В тексте радиограммы содержится 118 символов, каждый символ несет 1 байт информации. Следовательно, должно быть передано 118 байт информации.

---

Смотрите также файлы

• А департамент потребительского рынке областной администрации.docx

• Тема дружбы и любви в произведение Маленький принц А. С. Экзюпери план о чем произведение Маленький принц.docx

• На примере задач рынка недвижимости ответьте на следующие вопросы какие данные, подходящие под определение big data, фиксируютсямогут фиксироваться в исследуемой предметной области.pdf

• Существует одна старинная легенда. В ней рассказывается о великой материнской любви. Был у матери единственный сын. Взял он в жены хоть и красивую, но злую девушку и привел ее в дом жить.docx

• Курс лекций по дисциплине Техническая механика для студентов заочного отделения специальности.pdf