ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 04.02.2024
Просмотров: 39
Скачиваний: 1
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
вероятности имеем:
????(????) = ∑????(????i) · ????????i(????);
????(????) = 0,75 * 0,9 + 0,25 * 0,8 = 0,875
Ответ: 0,875.
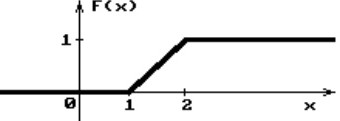
Найти ????(????). Решение.
Найдем функцию распределения ????(????). При ???? < 1 ????(????) = 0
При 1 ≤ ???? ≤ 2 график проходит через точки (1,0) и (2,1).
Уравнение прямой, проходящее через 2 точки (????1; ????1) (????2; ????2), имеет вид:
???? − ????1
????2 − ????1
= ???? − ????1
????2 − ????1
Подставляя в него координаты точек (1,0) и (2,1), получаем:
???? − 1 = ???? − 0 ; ???? − 1 ????
???? = ???? − 1
2 − 1
1 − 0
1 = 1 ;
Таким образом, при 1 ≤ ???? ≤ 2 ????(????) = ???? − 1
При ???? > 2 ????(????) = 1
Функция распределения примет вид:
0 ???? < 1
????(????) = {???? − 1 1 ≤ ???? ≤ 2
1 ???? > 2
Плотность распределения ƒ(????)
= ???? (????):
+∞
????(????) = ∫ ????ƒ(????)????????
−∞
1 2 ∞ 1 2 ∞
????(????) = ∫ ???? · 0 ???????? + ∫ ???? · 1 ???????? + ∫ ???? · 0 ???????? = ∫ 0 ???????? + ∫ ???? ???????? + ∫ 0 ???????? =
−∞ 1
2
????2 2
−∞ 1 2
22 12
= 0 + ( 2 )|
1
+ 0 =
2 − 2 = 1,5
Ответ: ????(????) = 1,5.
Решение.
Применим классическое определение вероятности:
????(????) = ????
????
???? − число благоприятных исходов;
???? − число всевозможных исходов;
Всего имеется 15 шаров (9 белых и 6 черных), из них вынимают два
=> ???? = ????2 = 15!
= 14 * 15 = 105
15 2! * 13!
1 * 2
???? = ????!
− ???? ????
???? ????! (???? − ????)!
???? − оба вынутых шара окажутся белыми.
???? = ????0 · ????2 = 6!
* 9!
= 1 * 36 = 36
6 9 0! * 6!
2! * 7!
Ответ: 0,3429.
????(????) = 36
105
= 12 ≈ 0,3429
35
Решение.
Случайная величина X − сумма чистого выигрыша, может принимать три значения: - 100 руб. (если студент не выиграет, а фактически проиграет
100 руб., уплаченные им за билет), 900 руб. и 2900 руб. (фактический выигрыш уменьшается на 100 руб. - на стоимость билета). Первому результату благоприятствуют 47 случаев из 50, второму - 2, а третьему - один. Поэтому их вероятности таковы:
????1
(???? = −100) = 47 = 0,94
50
????2
(???? = 900) = 2
50
= 0,04
????3
(???? = 2900) = 1
50
= 0,02
Закон распределения примет вид:
Ответ:
Решение.
Пусть ???? телевизоров изготовлено второй партией, тогда первой партией изготовлено 2???? телевизоров.
???? + 2???? = 1; 3???? = 1; ???? = 1
3
????1 − телевизор изготовлен первой партией.
????(????1) = 2/3
????2 − телевизор изготовлен второй партией.
????(????2) = 1/3
???? − купленный телевизор будет надежным. Условные вероятности этого события равны:
????????1 (????) = 0,9; ????????2 (????) = 0,8
По формуле полной вероятности имеем:
????(????) = ∑????(????i) · ????????i(
????);
( ) 2 1 13
???? ???? = 3 * 0,9 + 3 * 0,8 = 15 ≈ 0,8667
Ответ: 0,8667.
Решение.
Случайная величина X − размер выигрыша, может принимать четыре значения: 100, 200, 1000, 2000 р. Первому результату благоприятствуют 400 случаев из 1000, второму - 300, третьему – 200 и четвертому 100. Поэтому их вероятности таковы:
????1
????2
(???? = 100) = 400
1000
(???? = 200) = 300
1000
= 0,4
= 0,3
????3
????4
(???? = 1000) = 200
1000
(???? = 2000) = 100
1000
= 0,2
= 0,1
Закон распределения примет вид:
Математическое ожидание:
????(X) = ∑ ????i????i
????(X) = 100 · 0,4 + 200 · 0,3 + 1000 · 0,2 + 2000 · 0,1 = 500
Ответ: средний размер выигрыша для посетителя парка, купившего один билет, составит 500 рублей.
????(????) = ∑????(????i) · ????????i(????);
????(????) = 0,75 * 0,9 + 0,25 * 0,8 = 0,875
Ответ: 0,875.
-
График функции распределения случайной величины имеет вид:
Найти ????(????). Решение.
Найдем функцию распределения ????(????). При ???? < 1 ????(????) = 0
При 1 ≤ ???? ≤ 2 график проходит через точки (1,0) и (2,1).
Уравнение прямой, проходящее через 2 точки (????1; ????1) (????2; ????2), имеет вид:
???? − ????1
????2 − ????1
= ???? − ????1
????2 − ????1Подставляя в него координаты точек (1,0) и (2,1), получаем:
???? − 1 = ???? − 0 ; ???? − 1 ????
???? = ???? − 1
2 − 1
1 − 0
1 = 1 ;
Таким образом, при 1 ≤ ???? ≤ 2 ????(????) = ???? − 1
При ???? > 2 ????(????) = 1
Функция распределения примет вид:
0 ???? < 1
????(????) = {???? − 1 1 ≤ ???? ≤ 2
1 ???? > 2
Плотность распределения ƒ(????)
= ???? (????):
| 0 | | ???? < 1 |
| ƒ(????) = {1 | | 1 ≤ ???? ≤ 2 |
| 0 Математическое ожидание: | | ???? > 2 |
+∞
????(????) = ∫ ????ƒ(????)????????
−∞
1 2 ∞ 1 2 ∞
????(????) = ∫ ???? · 0 ???????? + ∫ ???? · 1 ???????? + ∫ ???? · 0 ???????? = ∫ 0 ???????? + ∫ ???? ???????? + ∫ 0 ???????? =
−∞ 1
2
????2 2
−∞ 1 2
22 12 = 0 + ( 2 )|1
+ 0 =
2 − 2 = 1,5
Ответ: ????(????) = 1,5.
Вариант 4.
-
В урне 9 белых и 6 черных шаров. Из урны вынимают два шара. Какова вероятность того, что оба шара окажутся белыми?
Решение.
Применим классическое определение вероятности:
????(????) = ????????
???? − число благоприятных исходов;
???? − число всевозможных исходов;
Всего имеется 15 шаров (9 белых и 6 черных), из них вынимают два
=> ???? = ????2 = 15!
= 14 * 15 = 105
15 2! * 13!1 * 2
???? = ????!
− ???? ????
???? ????! (???? − ????)!
???? − оба вынутых шара окажутся белыми.
???? = ????0 · ????2 = 6!
* 9!
= 1 * 36 = 36
6 9 0! * 6!
2! * 7!
Ответ: 0,3429.
????(????) = 36
105= 12 ≈ 0,3429
35-
В студенческой группе организована лотерея. Разыгрываются две вещи стоимостью по 1000 руб. и одна стоимостью 3000 руб. Составить закон распределения суммы чистого выигрыша для студента, который приобрел один билет за 100 руб.; всего продано 50 билетов.
Решение.
Случайная величина X − сумма чистого выигрыша, может принимать три значения: - 100 руб. (если студент не выиграет, а фактически проиграет
100 руб., уплаченные им за билет), 900 руб. и 2900 руб. (фактический выигрыш уменьшается на 100 руб. - на стоимость билета). Первому результату благоприятствуют 47 случаев из 50, второму - 2, а третьему - один. Поэтому их вероятности таковы:
????1
(???? = −100) = 47 = 0,94
50????2
(???? = 900) = 2
50= 0,04
????3
(???? = 2900) = 1
50= 0,02
Закон распределения примет вид:
| ????i | -100 | 900 | 2900 |
| ????i | 0,94 | 0,04 | 0,02 |
Ответ:
| ????i | -100 | 900 | 2900 |
| ????i | 0,94 | 0,04 | 0,02 |
Вариант 5.
-
Завод изготовил две партии телевизоров. Первая партия телевизоров в два раза больше второй. Надежность телевизоров первой партии – 0,9, второй партии – 0,8. Определить вероятность того, что наугад купленный телевизор будет надежным.
Решение.
Пусть ???? телевизоров изготовлено второй партией, тогда первой партией изготовлено 2???? телевизоров.
???? + 2???? = 1; 3???? = 1; ???? = 13
????1 − телевизор изготовлен первой партией.
????(????1) = 2/3
????2 − телевизор изготовлен второй партией.
????(????2) = 1/3
???? − купленный телевизор будет надежным. Условные вероятности этого события равны:
????????1 (????) = 0,9; ????????2 (????) = 0,8
По формуле полной вероятности имеем:
????(????) = ∑????(????i) · ????????i(
????);
( ) 2 1 13
???? ???? = 3 * 0,9 + 3 * 0,8 = 15 ≈ 0,8667
Ответ: 0,8667.
-
В парке отдыха организована беспроигрышная лотерея. Имеется 1000 выигрышей, из них 400 – по 100 руб.; 300 – по 200 руб.; 200 – по 1000 руб. и 100 – по 2000 руб. Какой средний размер выигрыша для посетителя парка, купившего один билет?
Решение.
Случайная величина X − размер выигрыша, может принимать четыре значения: 100, 200, 1000, 2000 р. Первому результату благоприятствуют 400 случаев из 1000, второму - 300, третьему – 200 и четвертому 100. Поэтому их вероятности таковы:
????1
????2
(???? = 100) = 400
1000 (???? = 200) = 3001000
= 0,4
= 0,3
????3
????4
(???? = 1000) = 200
1000 (???? = 2000) = 1001000
= 0,2
= 0,1
Закон распределения примет вид:
| ????i | 100 | 200 | 1000 | 2000 |
| ????i | 0,4 | 0,3 | 0,2 | 0,1 |
Математическое ожидание:
????(X) = ∑ ????i????i
????(X) = 100 · 0,4 + 200 · 0,3 + 1000 · 0,2 + 2000 · 0,1 = 500
Ответ: средний размер выигрыша для посетителя парка, купившего один билет, составит 500 рублей.