Файл: Е. С. Тетерин 2021 г.docx

Министерство науки и высшего образования РФФедеральное государственное автономное образовательное учреждение высшего образования«Южно–Уральский государственный университет»(Национальный исследовательский университет)Институт открытого и дистанционного образованияПОЯСНИТЕЛЬНАЯ ЗАПИСКАК КУРСОВОй работе

по дисциплине Теория автоматического управления

ЮУрГУ– 09.03.01.2021.244. ПЗ КР

Нормоконтролер _________ А.Г. Калачева ____________________2021 г.	Руководитель _____________ К.М. Виноградов ____________________2021 г.
	Автор проекта, студент группы ДО–410 Е.С. Тетерин _____________________2021 г.
	Проект защищен с оценкой ____________ К.М. Виноградов ____________________2021 г.

Челябинск 2021Министерство науки и высшего образования РФФедеральное государственное автономное образовательное учреждение высшего образования«Южно–Уральский государственный университет»(Национальный исследовательский университет)Институт открытого и дистанционного образованияКафедра техники, технологии и строительстваНаправление «Информатика и вычислительная техника»УтверждаюЗаведующий кафедрой______________________________ 2021г.ЗАДАНИЕна курсовую работу студентаТетерин Евгений СергеевичГруппа ДО-4101 Дисциплина: Теория автоматического управления 2 Тема проекта: Замкнутая система автоматического управления3 Срок сдачи студентом законченной работы: ______________2021 г.

4. 
   Перечень вопросов, подлежащих разработке:
   

- Произвести выбор последовательного регулятора;

- Удовлетворять показателям качества в соответствие с вариантом задания.

5 Календарный план

Наименование разделов курсового проекта	Срок выполнения разделов проекта	Отметка о выполнении руководителя
Введение	Март 2021
1 часть	Март 2021
2 часть	Апрель 2021
Заключение, список использованной литературы	Апрель 2021

---

Руководитель проекта _____________________________// К.М. Виноградов(подпись)Студент _________________________// Е.С. Тетерин(подпись) АННОТАЦИЯТетерин Е.С. Теория автоматического управления. – Челябинск: ЮУрГУ, 2021. – 19 с. библиогр. список – 10 наим.Целью работы является для замкнутой системы автоматического управления (САУ) с отрицательной (единичной) обратной связью, произвести выбор последовательного регулятора (корректирующего устройства).

ОГЛАВЛЕНИЕ

ВВЕДЕНИЕ

Теория автоматического управления (ТАУ) является базовой основой кибернетики или науки об управлении – одной из относительно молодых областей науки. Теория управления, хотя и прошла яркий путь своего развития, но в настоящее время продолжает интенсивно развиваться в сторону создания теории интеллектуальных систем управления – предельной формации парадигмы теории управления.Прикладную или инженерную ТАУ сегодня именуют «классической», подчеркивая этим определенную завершенность форм ее развития как науки об управлении. Классическая ТАУ, преследуя цель «оптимизации в малом», решает задачи оптимизации и адаптации при малых отклонениях относительно заданного режима работы системы управления.Теория автоматического управления (ТАУ) относится к классу важнейших общеспециальных дисциплин, входящих во все типовые программы инженерного образования, ТАУ изучает процессы управления, методы исследования и основы проектирования систем автоматического управления (САУ). ТАУ изучает принципы построения САУ, закономерности протекающих в них процессов в целях построения работоспособных и точных САУ. Методами ТАУ осуществляются анализ и синтез САУ.В данном курсовом проекте решаются задачи, связанные с анализом и синтезом САУ, относящиеся к «классической» ТАУ.Исходными данными для выполнения курсового проекта являются структурная схема замкнутой автоматической системы регулирования, параметры входящих в нее звеньев и требуемые показатели качества.

---

1 Для замкнутой системы автоматического управления (САУ) с отрицательной (единичной) обратной связью, структурная схема которой в разомкнутом состоянии изображена на рисунке 1 (передаточные функции звеньев, согласно варианта задания, представлены в таблице 1), произвести выбор последовательного регулятора (корректирующего устройства), исходя из требований, что проектируемая система должна: 1.1 воспроизводить постоянное входное воздействие с нулевой установившейся ошибкой (система должна иметь астатизм первого порядка); 1.2 удовлетворять показателям качества в соответствие с вариантом задания (таблица 2).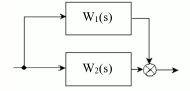Рисунок 1 – Структурная схема исходной САУ в разомкнутом состоянииТаблица 1 – Передаточные функции звеньев исходной системы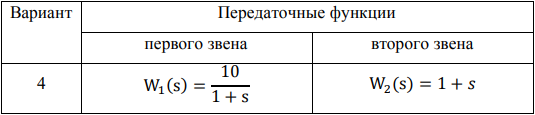Таблица 2 – Показатели качества проектируемой САУ2 Провести анализ полученной САУ. 2.1 Подтвердить факт, что полученная САУ с последовательным регулятором (корректирующим устройством) удовлетворяет заданным показателям качества в соответствие с вариантом задания. Для этого определить и построить график переходной характеристики системы. Переходную характеристику системы возможно вычислить аналитически с помощью обратного преобразования Лапласа. Графики полученной функции можно построить с помощью одной из программ SMath Studio, Excel, OpenOffice Calc или других аналогичных. 2.2 Исследовать устойчивость полученной САУ.Выполнение курсовой работы проводится в два этапа:– исследование линейной системы автоматического регулирования;– синтез корректирующего устройства, построение переходного процесса скорректированной системы и оценка качества регулирования.

1 Выбор последовательного регулятора

Исходная структурная замкнутой системы будет иметь вид:

---

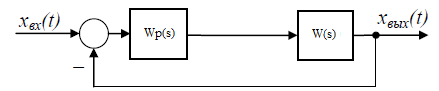
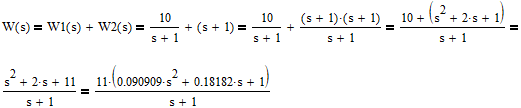
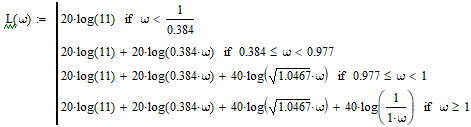
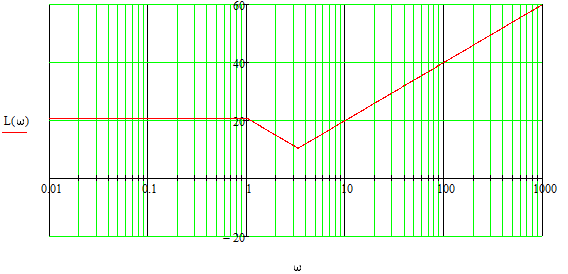
Рис. 1.1 – Структурная схема исследуемой системыПри этом, структура блока W(s) имеет вид:Рис. 1.2 – Структура САУ в разомкнутом состоянии без регулятораОпределим ПФ разомкнутой САУ без регулятора и сведём её к стандартному виду:Запишем уравнение асимптотической ЛАЧХ и построим ЛАЧХ данного звена:Рис. 1.3 – Асимптотическая ЛАЧХ разомкнутой нескорректированной системыДалее построим желаемую ЛАЧХ.При построении желаемой ЛАЧХ выделяют 3 участка.Низкочастотная область желаемой ЛАЧХ строится исходя из требований к точности скорректированной системы. По условию, система должна исключать статическую ошибку; при этом требования к величине скоростной ошибки не указаны. Поэтому вводим в систему интегратор. 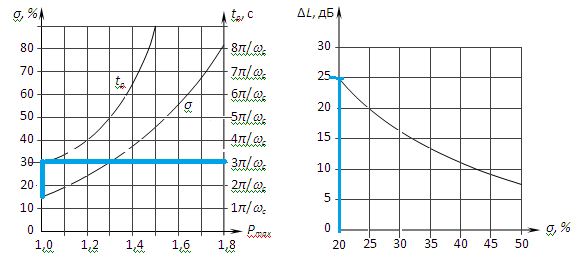Это означает, что низкочастотный участок желаемой ЛАЧХ должен идти под наклоном «-20 дБ/дек»Среднечастотный участок желаемой ЛАЧХ строится по требованиям переходного процесса с использованием номограмм Солодовникова:а) б)Рисунок 1.4 – Номограммы СолодовниковаПо условию, перерегулирование σ не должно превышать 17%. 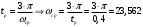По номограмме Солодовникова (а) определяем формулу для зависимости времени регулирования tp и частоты среза ωср:По номограмме Солодовникова (б) определяем протяжённость среднечастотного участка: ΔL = 25 дБ (в случае надобности, его можно продлить).Высокочастотный участок желаемой ЛАЧХ не влияет на динамические свойства системы, и строится из удобства расчёта звена КУ.Также отметим, что ЛАЧХ желаемой системы не может иметь в высокочастотной области наклон «+20 дБ/дек», т.к. такое звено не может быть физически реализовано.

---

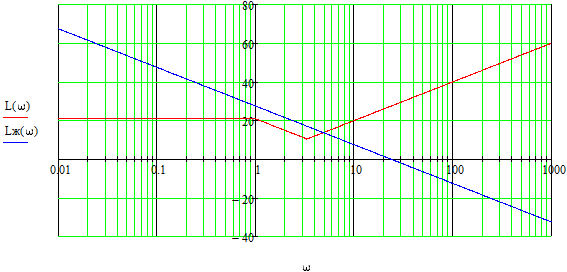
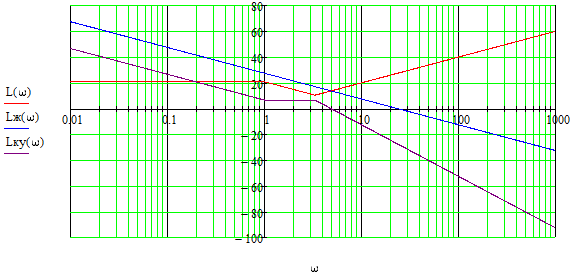
Высокочастотный участок желаемой ЛАЧХ продолжает идти под наклоном «-20 дБ/дек»Строим желаемую ЛАЧХ:Рисунок 1.5 – Желаемая ЛАЧХЛАЧХ КУ находим, вычитая из желаемой ЛАЧХ исходную располагаемую ЛАЧХ:Рисунок 1.6 – ЛАЧХ КУПо ЛАЧХ КУ восстанавливаем ПФ последовательного КУ:

2 Основная часть

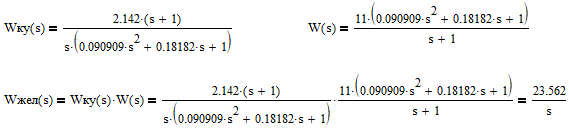
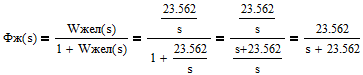
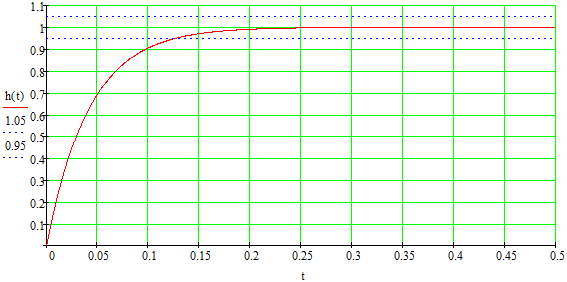
Рис. 2.1 – Структурная схема исследуемой системыТогда ПФ желаемой разомкнутой системы примет вид:Тогда эквивалентная ПФ замкнутой скорректированной системы примет вид: Чтобы найти уравнение переходной характеристики h(t), нужно домножить ПФ замкнутой системы на 1/s (изображение единичного ступенчатого сигнала по Лапласу) и выполнить обратные преобразования Лапласа полученного выражения:Рис. 2.2 – Переходная характеристика замкнутой скорректированной системыУстановившееся значение составляет 1, следовательно, статическая ошибка отсутствует.Время регулирования составляет: t_p = 0,125 c < 0,4 c.Перерегулирование составляет: σ = 0% < 17%.Требования, установленные в техническом задании, выполняются.Далее оценим устойчивость замкнутой системы.Выделяем характеристический полином замкнутой системы – знаменатель ПФ замкнутой системы:По критерию Гурвица, для систем с полиномом 1 порядка, необходимым и достаточным условием устойчивости является положительность всех коэффициентов характеристического полинома.Условие выполняется; скорректированная система устойчива.

---