1. Типовые законы управления.
Для выбора того или иного закона управления необходимо знать, какое влияние оказывает каждое из слагаемых, входящее в закон управления, на устойчивость и качество управления.



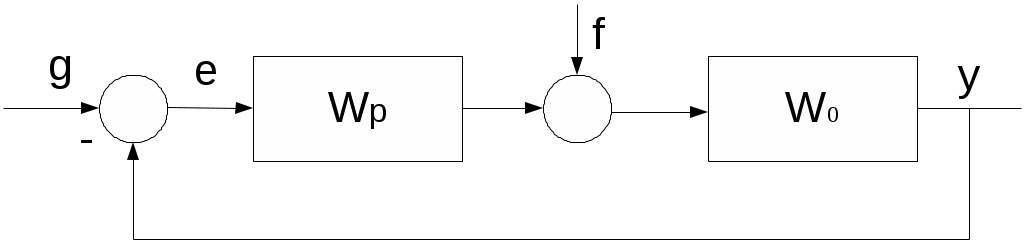
Рис. 1 Типовая схема системы управления
Для выяснения этого вопроса рассмотрим систему управления (рис.1.) при типовых законах управления, когда передаточная функция объекта имеет вид

.

П-закон. При П-законе передаточная функция регулятора W_р(p) = k_п, и передаточная функция разомкнутой системы имеет вид

.

Характеристическое уравнение замкнутой системы



имеет корни

.

Отсюда видно что если объект управления является колебательным звеном (0<ξ<1), то замкнутая система при любом k_п>0 является также колебательным звеном, и степень колебательности c ростом k_п возрастает.

Когда объект является апериодическим звеном 2-го порядка

( 1≥ ξ≥0), замкнутая система также является апериодическим звеном 2-го порядка при k_п ≤ ξ²-1 и колебательным звеном при k_п> ξ²-1.

Передаточная функция ошибки по задающему воздействию имеет вид

.

Видно, что при П-регуляторе рассматриваемая система является статической, и статическая ошибка убывает с ростом k_п. Однако, начиная с k_п = ξ²-1, с ростом k_п увеличивается степень колебательности.

ПИ-закон: В этом случае , передаточная функция разомкнутой системы имеет вид

---

,

и характеристическое уравнение имеет вид

.

Коэффициенты этого уравнения положительны, определитель Гурвица 2-го порядка



при больше нуля и система устойчива, а при -меньше или равен нулю, что нарушает устойчивость системы. Следовательно, увеличение коэффициента при интегральном члене приводит к неустойчивости системы. Естественно ожидать, что с увеличением k_и в области устойчивости запасы устойчивости убывают, а степень колебательности увеличивается.

Передаточная функция относительно ошибки для системы с ПИ-регулятором имеет вид

.

Отсюда видно, что при включении интегрального слагаемого в закон управления система становится астатической, и с увеличением k_и уменьшается скоростная ошибка. Однако при этом ухудшается качество системы в переходном режиме, и с определенного k_и система становится неустойчивой.
2. Настройка параметров регуляторов по корневым показателям качества
2.1. Показатели качества и типовые воздействия.
Наиболее полной характеристикой качества системы управления является поведение сигнала ошибки e = g – y во времени (рис.2, а).

Так как y = W_yg(p)g + W_yf(p)f, где W_yg(p) и W_yf(p) – передаточные функции относительно выхода y и входов g и f соответственно, то

e = g – y = W_eg(p)g + W_yf(p)f (1)

Здесь W_eg(p) = 1 - W_yg(p) - передаточная функция относительно выхода e и входа g, которая называется передаточной функции ошибки по задающему воздействию.



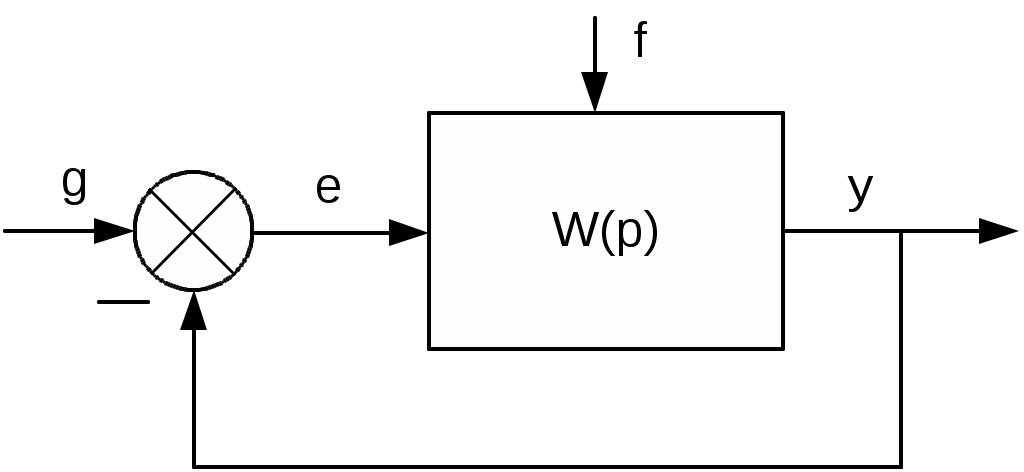
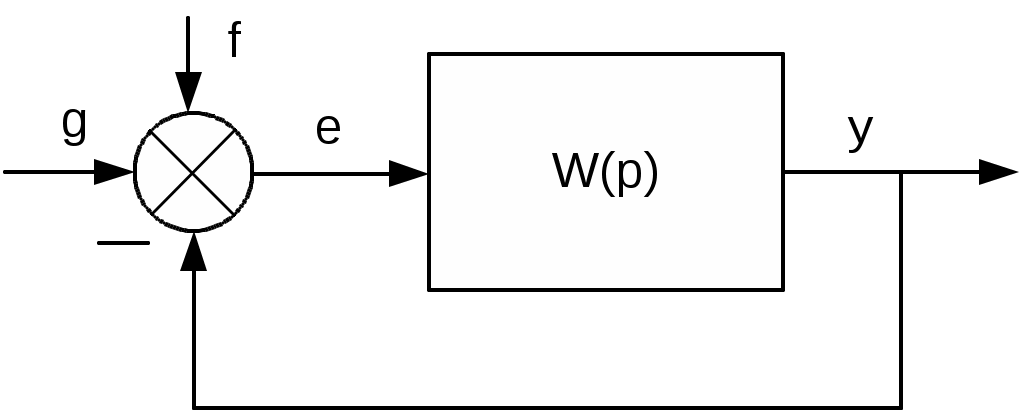
а б
Рис.2. Схемы приложения возмущений; возмущение приложено не на входе (а) и на выходе (б) сравнивающего устройства

---

Используя передаточную функцию W_ef(p) относительно выхода e и входа f, называемую передаточной функцией по возмущению, формулу (1) можно записать в виде

e = W_eg(p)g + W_ef(p)f (2)

Эта формула совпадает с (1) определяет ошибку только в том случае, когда возмущение f приложено не на входе сравнивающего устройства, как это показано на рис. 2, а. Только в этом случае W_ef(p) = - W_yf(p). Если возмущение приложено на входе сравнивающего устройства (рис.2, б), то для определения ошибки нужно пользоваться формулой (1). Как видно из (1)-(3), ошибку можно представить в виде суммы

e = e_g + e_f, (3)

где e_g = W_eg(p)g, e_f = W_ef(p)f,

или, если возмущение приложено на входе сравнивающего устройства (в точке приложения задающего воздействия),

e_f = - W_yf(p)f. (4)

Первая составляющая e_g называется ошибкой от задающего воздействия, вторая составляющая – ошибкой от возмущения. Если на систему действует несколько возмущений, то ошибка от возмущений будет равна сумме ошибок от каждого возмущения.

Ошибка e, являясь функцией от времени, не очень удобна для оценки качества систем управления. Поэтому на практике при оценке качества чаще используют числовые показатели, которые прямо или косвенно характеризуют точность воспроизведения заданного движения. Показатели качества делятся на показатели качества в переходном режиме и показатели качества в установившемся режиме.

О качестве системы управления имеет смысл говорить, если она устойчива. Поэтому показатели качества определяют при предположении, что система устойчива.

Ошибка e зависит как от свойства системы управления, так и от внешнего воздействия. По этой причине показатели качества как характеристики свойства системы определяют при определенных внешних воздействиях, называемых типовыми.

При оценке качества в переходном режиме в качестве типового воздействия используют ступенчатую функцию A*1(t) (А - константа), а при оценке качества в установившемся режиме – полиномы времени t: At, At², ...
2.2. Показатели качества в переходном режиме
Показатели качества в переходном режиме делятся на прямые и косвенные показатели. Последние делятся на корневые, частотные и интегральные.

---

2.2.1. Прямые показатели качества
Как отмечалось, при определении показателей качества в переходном режиме в качестве типового воздействия используется ступенчатое воздействие А*1(t). Характер переходного процесса не зависит от величины А. Реакция системы y на входное воздействие А*1(t) пропорциональна переходной функции h(t), являющейся реакцией системы на единичное ступенчатое воздействие 1(t): y = Ah(t). Поэтому обычно принимают А = 1.

При ступенчатом воздействии ошибка

e = 1(t) – h(t)

отличается от переходной функции на постоянную величину. Поэтому при оценке качества в переходном режиме вместо сигнала ошибки также используют переходную функцию.

Прямыми показателями качества называют показатели, которые получаются непосредственно по переходной характеристике. Из прямых показателей качества наиболее часто используют время регулирования и перерегулирование.

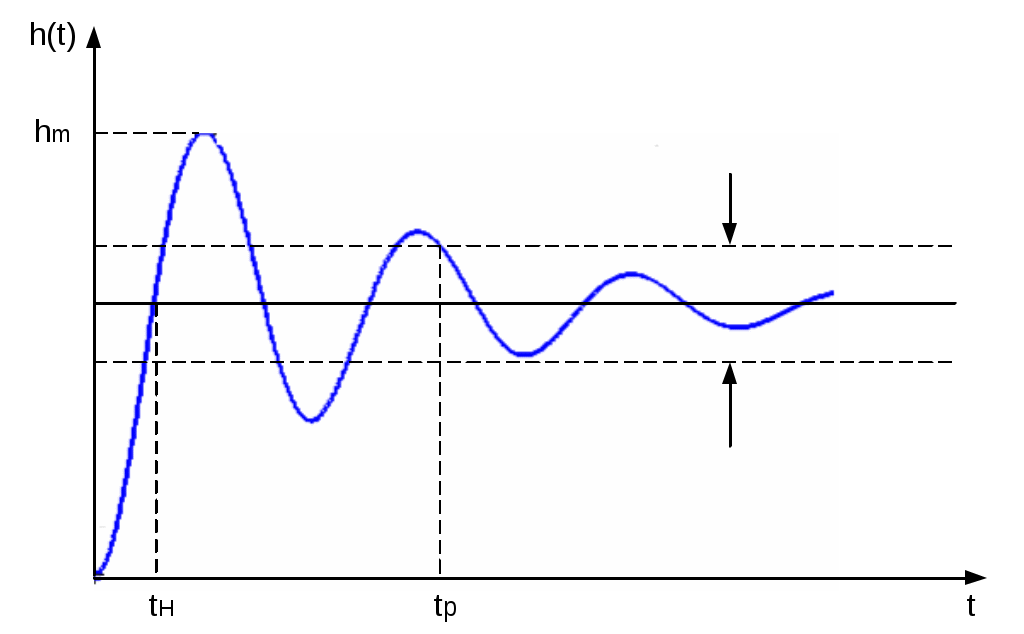
Временем регулирования t_p называется минимальное время, по истечении которого (с момента подачи ступенчатого воздействия) отклонение выходной величины от установившегося значения h(∞) не превышает некоторой заданной величины Δ.

Математически это определение можно записать следующим образом:

t_p = min {Tр: |h(t) – h(∞)| ≤ Δ, t ≥ Tр}.

Обычно принимают Δ = (0,05÷0,1) h(∞).

Для определения времени регулирования по переходной характеристике можно провести по обе стороны по прямой h(t) = h(∞) на расстоянии Δ параллельные прямые (рис.3). И время регулирования определяется как время t_p, когда переходная характеристика в последний раз пересекает любую из приведенных прямых.


h(∞)

2


Рис. 3. Переходная характеристика
Не играют роли детали очертания кривой переходной процесса, а важно, чтобы она не выходила за определенные границы (2).

Быстродействие определяется временем вхождения в 5%-ую трубку точности самой медленной затухающей свободной cоставляющей.

---

Таким образом:

.

Перерегулирование обозначают буквой σ и определяют следующим образом

,

где h_m – максимальное значение переходной функции.

Иначе говоря, перерегулированием называется максимальное отклонение переходной функции от установившегося значения h(∞), выраженное в процентах по отношению к h(∞).

Если ступенчатое воздействие подать на вход, где действует возмущение (f(t) = A₀*1(t)), то установившееся значение выходной переменной может быть малым или равным нулю, и кривая переходного процесса будет иметь вид, показанный на рис.4.


2


Рис.4 Кривая переходного процесса (по возмущению)
В этом случае перерегулирование определяется как максимальное отклонение, выраженное в процентах по отношению к величине входного воздействия:



Кроме времени регулирования и перерегулирования, иногда также рассматривают число колебаний за время регулирования t_p и время нарастания t_и – время первого достижения установившегося значения (см. рис. 3.).

Число колебаний за время регулирования N_к можно рассматривать как прямой численный показатель интуитивного понятия «колебательность» системы. Когда говорят, что колебательность системы повышается, как правило, имеют в виду, что увеличивается амплитуда или частота колебаний, колебания медленнее затухают. Во всех этих случаях N_к увеличивается.

Переходную характеристику проще всего построить с помощью компьютера, решив дифференциальное уравнение при единичной входной функции и нулевых начальных условиях.

---

Смотрите также файлы

• Дыбыс, дыбысты сипаттамалары, акустикалы резонанс, жаыры Оу бадарламасына сйкес оыту масаттары.docx

• Овтеты овтеты овтеты овтеты овтеты овтеты овтеты овтеты овтеты овтеты овтеты овтеты овтеты.docx

• Доклад на тему Лето 2019. Новые формы работы с детьми в лагере разновозрастных отрядов. Проблемы организации отдыха, оздоровления и занятости детей и подростков в каникулярный период.doc

• Делиханов Ахмед Адамович.doc

• Составитель учитель начальных классов Петухова М. Г. Технологическая карта по математике.docx