Файл: Методические указания к выполнению курсовых работ. Северодвинск 2017.docx
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 04.02.2024
Просмотров: 91
Скачиваний: 1
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
-
ТЕПЛОВОЙ РАСЧЁТ ТЕПЛООБМЕННОГО АППАРАТА
Тепловой расчёт выполняется на основе совместного решения двух уравнений.
-
Уравнение теплового баланса:
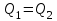 ,
,где:
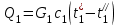 - количество теплоты, отдаваемое охлаждаемым теплоносителем в единицу времени;
- количество теплоты, отдаваемое охлаждаемым теплоносителем в единицу времени;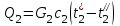 - количество теплоты, воспринимаемое охлаждающим теплоносителем в единицу времени;
- количество теплоты, воспринимаемое охлаждающим теплоносителем в единицу времени;G1, G2 – массовые расходы теплоносителей, кг/с;
с1, с2 – удельные теплоёмкости теплоносителей, Дж/ (кгК);
t/ - температуры на входе, t// - температуры на выходе.
-
Уравнение теплопередачи:
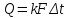 ,
,где:
k – коэффициент теплопередачи, Вт/(м2К);
F – площадь поверхности теплообмена, м2;
t – средний логарифмический температурный напор.
Коэффициент теплопередачи определяется по формуле:
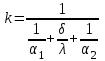 ,
,где:
1, 2 – коэффициенты теплоотдачи от охлаждаемого теплоносителя к поверхности стенки и от поверхности к охлаждающему теплоносителю;
- толщина стенки, разделяющей теплоносители;
- коэффициент теплопроводности материала стенки.
Частные коэффициенты теплоотдачи 1 и 2 зависят от многих факторов (свойства теплоносителей, конфигурация и материал поверхности теплообмена) и ввиду сложности процессов конвективного теплообмена как правило не могут быть выражены аналитически. Они рассчитываются с помощью критериальных уравнений, полученных при обработке экспериментальных данных на основе теории подобия. Критерии подобия, входящие в критериальное уравнение, зависят от геометрических характеристик канала, по которому протекает теплоноситель, и от свойств теплоносителей, которые определяются в первую очередь температурой. Температура, принимаемая за определяющую, должна наиболее полно отражать физическую сущность процесса теплопередачи. Чаще всего при расчёте теплообменных аппаратов в качестве определяющей принимается среднеарифметическая температура теплоносителя:
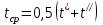
.
Иногда целесообразно в качестве определяющей выбирать температуру стенки.
Средний логарифмический температурный напор t зависит от схемы движения теплоносителей.
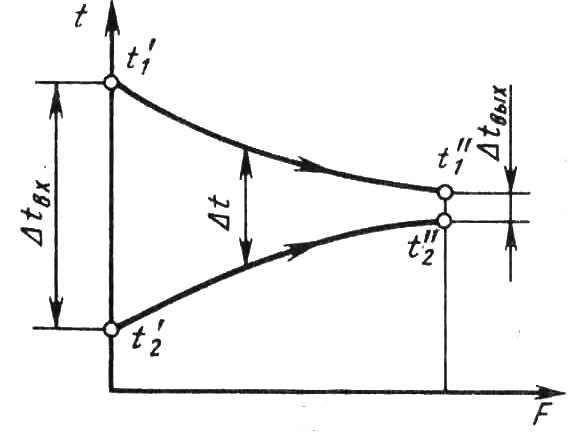
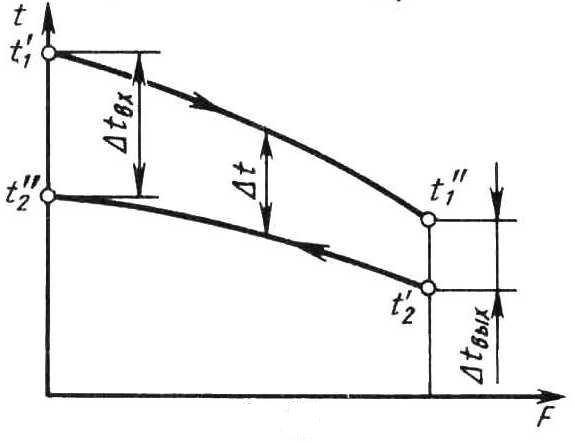
а) б)
Рис. 6
Для схемы прямотока (рис. 6, а) применяется формула:
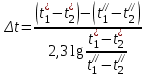 ,
,а для схемы противотока (рис. 6, б) – формула:
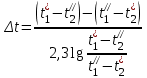 .
.При более сложных схемах движения теплоносителей математические выкладки значительно усложняются, поэтому температурный напор находят по формуле противотока с внесением поправочного множителя , который определяется с помощью специальных графиков. Множитель < 1, так как температурный напор при схеме противотока является максимальным при прочих равных условиях (для него = 1), соответственно температурный напор при схеме прямотока является минимальным.
Алгоритм теплового расчёта охладителя из круглых трубок с сегментными перегородками.
Исходными данными являются объёмные расходы теплоносителей W1 и W2, температуры охлаждаемого теплоносителя на входе и на выходе t1/ и t1// и температура охлаждающего теплоносителя на входе t2/.
-
Рассчитывается средняя температура охлаждаемого теплоносителя:
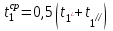
При данной температуре определяются параметры теплоносителя: 1, с1, 1, 1, Pr1.
-
Количество теплоты, отдаваемое охлаждаемым теплоносителем в единицу времени:
 ,
,массовый расход находится через объёмный:
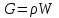 .
.-
Определяется температура охлаждающего теплоносителя на выходе:
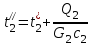 ,
,Q2 = Q1 (уравнение теплового баланса). Нужно найти с2 и 2 (ля определения G2) при средней температуре охлаждающего теплоносителя
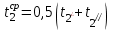
, которая в свою очередь зависит от искомой t2//. В этом случае используется метод последовательных приближений. Искомая температура t2// лежит в интервале [t2/; t1ср]. Берётся какое-либо значение {t2//} из этого интервала.
3.1) Рассчитывается:
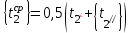 .
.3.2) При этом значении определяются с2 и 2 и рассчитывается:
 .
.3.3) Рассчитывается погрешность:
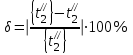 .
.Если < 5%, то полученное значение t2// принимается за истинную температуру охлаждаемого теплоносителя на выходе. Если же > 5%, то делается следующее приближение: полученное значение t2// принимается за {t2//}, и расчёт повторяется с пункта 3.1).
-
Рассчитывается средняя температура t2ср :
 .
.При данной температуре определяются параметры охлаждающего теплоносителя: 2, с2, 2, 2, Pr2.
-
Принимается скорость охлаждающего теплоносителя в трубках 2 , а так же наружный и внутренний диаметр трубок dнар и dвн. Толщина стенки ст = (dнар - dвн)/2. -
Рассчитывается число Рейнольдса для охлаждающего теплоносителя:
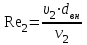
-
Температура стенки со стороны охлаждающего теплоносителя t2ст лежит в интервале [t2ср; t1ср]. Этот интервал разбивается с таким шагом, чтобы в него входило 10 - 15 значений температур. Эти значения t2ст1, t2ст2, … t2стnзаносятся в таблицу:
| № | t2ст | Pr2ст | 2 | q2 | ст | t1ст | Pr1ст | 1 | q1 |
| 1 | | | | | | | | | |
| 2 | | | | | | | | | |
| … | | | | | | | | | |
| n | | | | | | | | | |
-
Определяются для значений t2ст1, t2ст2, … t2стn числа Прандтля Pr2ст и заносятся в таблицу. -
По критериальному уравнению теплоотдачи для движения охлаждающего теплоносителя в трубках:
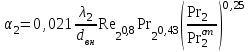
рассчитываются значения коэффициента теплоотдачи 21, 22, … 2n и заносятся в таблицу.
-
Определяется плотность теплового потока внутри трубок:
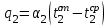 ,
,значения q21, q22, … , q2n заносятся в таблицу.
-
Рассчитывается температура стенки со стороны охлаждаемого теплоносителя:
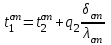 .
.Для этого для выбранного материала трубок определяются значения коэффициента теплопроводности ст при всех значениях t2ст1, t2ст2, … t2стn. Полученные значения температуры стенки со стороны охлаждаемого теплоносителя t1ст1, t1ст2, … t1стn заносятся в таблицу.
12. Принимается скорость охлаждаемого теплоносителя в межтрубном пространстве 1 и определяется минимальное расстояние между трубками .Для трубок 101 мм принято = 3,5 мм, а для трубок 161 мм принято = 5 мм.
13. Рассчитывается число Рейнольдса для охлаждаемого теплоносителя:
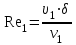 .
.-
Определяются для значений t1ст1, t1ст2, … t1стn числа Прандтля Pr1ст и заносятся в таблицу.
15. По критериальному уравнению теплоотдачи для движения охлаждаемого теплоносителя между трубками:
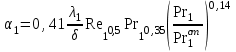
рассчитываются значения коэффициента теплоотдачи 11, 12, … 1n и заносятся в таблицу.
16. Определяется плотность теплового потока в межтрубном пространстве:
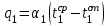 ,
,значения q11
, q12, … , q1n заносятся в таблицу.
-
По табличным данным строятся графики функций q2 = f(t2ст) и q1 = f(t2ст). На пересечении графиков находится искомая температура стенки со стороны охлаждающего теплоносителя t2ст.
Далее уже для найденной t2стпо пунктам 8/, 9/, 10/, 11/, 14/, 15/, 16/ производится расчёт истинных значений соответствующих величин.
-
Рассчитывается коэффициент теплопередачи:
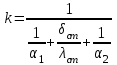 .
.-
Рассчитывается средний логарифмический температурный напор:
 .
.-
Рассчитывается площадь поверхности теплообмена:
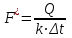 .
.-
С учётом поправки на загрязнение:
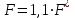 .
.-
Принимается число ходов охлаждающего теплоносителя в трубках z2 (1, 2, 4, … - имеет смысл для начала принять наименьшее значение, 1 или 2) и коэффициент заполнения трубной решётки = 0,7… 0,85. Чем больше ходов, тем меньше значение . -
Рассчитывается количество трубок ТОА:
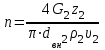 .
.-
Шаг разбивки по треугольнику:
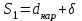 .
.-
Рассчитывается площадь трубной решётки:
 .
.-
Определяется внутренний диаметр корпуса ТОА:
 .
.-
Определяется длина трубок между трубными досками:
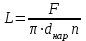 .
.-
Рассчитывается относительный диаметр ТОА:
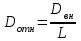 .
.Если Dотн укладывается в интервал [0,3 … 0,8], то всё в порядке, если же нет, следует вернуться к пункту 22 и взять большее количество ходов z2, а затем пересчитать для этого количества величины по пунктам 23, 25, 26, 27, 28 и снова проверить соответствие Dотн интервалу.