Тема: «Формулы приведения»

УМК А.Г. Мерзляк, Д.А. Номировский, В.М. Поляков «Алгебра и начала математического анализа 10 класс»

Тип урока: открытие новых знаний

Цели урока: вывод формул приведения; формирование умений и навыков применения формул приведения при преобразовании тригонометрических выражений.

Планируемые результаты (с позиции учащихся):

1. 
   Применяю формулы сложения для вывода формул приведения.
   
2. 
   Формулирую правило применения формул приведения.
   
3. 
   Применяю формулы приведения для упрощения тригонометрических выражений.
   

Технология (прием технологии): технология проблемного обучения.

Этапы урока	Время	Деятельность учителя	Деятельность ученика
Организационный момент (мотивация к учебной деятельности)	2 мин.	Здравствуйте! Для начала давайте подарим друг другу частичку доброты. Улыбнитесь соседу по парте. Спасибо. Присаживайтесь. Тема урока сегодня «Формулы приведения». Они необходимы для упрощения/преобразования тригонометрических выражений и вычисления значений тригонометрических функций больших углов. Их 32! Испугались? Заучивать их все не нужно. Достаточно будет знать правило и научится его применять. Попробуйте сформулировать цель урока.	Улыбаются друг другу. Садятся за парты. Записывают тему урока. - Научиться использовать формулы приведения для упрощения тригонометрических выражений и вычисления углов.
Актуализация знаний.	5 мин	Но начнём работу мы не с новой темы, а с повторения. Поиграем в «перестрелку». Правила такие. Вы называете угол (хоть в градусах, хоть в радианах) и имя ученика, который должен ответить в какой четверти находится угол. Если ученик ответил верно, то право выстрела переходит к нему, если нет, то возвращается к первому «стрелку». Правила понятны? Начинаем… После 5-6 выстрелов, учитель усложняет задачу. Просит, чтобы определяли знак тригонометрической функции угла. Например, cos189º<0, т.к. 189º находится в 3 четверти и значение косинуса там отрицательно. 5-6 выстрелов. Молодцы! Какую тему мы изучали на прошлых уроках? Для чего их используют? Запишите, пожалуйста, формулы сложения на доске. (косинус разности/суммы, синус разности/суммы, тангенс разности/суммы)	Играют в «перестрелку». Определяют, в какой четверти находится угол. После усложнения игры, определяют знак тригонометрической функции. Отвечают на вопрос - Формулы сложения. -Их используют для нахождения значений тригонометрических функций суммы или разности аргументов, для упрощения выражений. Записывают формулы на доске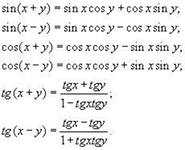
Постановка учебной задачи.	6 мин	Теперь делимся на группы по 4 человека и с помощь формул сложения упрощаем выражения. Угол α – острый. См. приложение Задание 1.Затем записываем ответ в таблицу. Приложение 2.	Делятся на группы. Каждый член группы по очереди выполняет задание. Все члены группы обсуждают и фиксируют решение в тетрадку. И на доске в таблицу
Построение проекта выхода из затруднения («открытие» нового знания)	3 мин	Ребята, посмотрите на получившиеся результаты внимательно. Заметили ли вы закономерности в таблице при помощи, которых можно выразить синус, косинус, тангенс, котангенс указанных через угол α? А от чего зависит знак правой части формулы?	Ребята высказывают свои мнения. -Если в левой части формулы угол имеет вид π/2±α или 3π/2±α, то синус меняется на косинус, тангенс на котангенс и наоборот. Если же угол в левой части формулы имеет вид π±α,2π±α, то замены не происходит. -Знак зависит от того, в какой четверти лежит угол в левой части формулы.
Первичное закрепление во внешней речи.	2 мин	Попробуйте сформулировать правило. Учитель обращает внимание на то, что α-острый угол. Мнемоническое правило (мнемоника – искусство запоминания). Достаточно задать себе два вопроса: 1. Меняется ли функция? Если в формуле присутствуют углы π/2  или  3π/2­­­ - это углы вертикальной оси, киваем головой по вертикали и сами себе отвечаем: «Да», если же присутствуют углы горизонтальной оси π или 2π, то киваем головой по горизонтали и получаем ответ: «Нет». 2. Какой знак надо поставить в правой части формулы? Знак определяем по левой части. Смотрим, в какую четверть попадает угол, и вспоминаем, какой знак в этой четверти имеет функция, стоящая в левой части. Повторите правило соседу по парте.	Ученики формулируют правило. В правой части равенства ставят, тот знак, который имеет левая часть при условии, что α-острый угол. Если в левой части формулы угол равен π/2±α,3π/2±α, то синус меняется на косинус, косинус – на синус, тангенс – на котангенс и котангенс – на тангенс. Если угол равен π±α, то замены функции не происходит. Повторяют правило с соседом.
Самостоятельная работа с проверкой по эталону.	8 мин	Если нет вопросов, то перейдём к тренировке «ручейком». Каждый ученик получает задание на карточке и решает его. См. приложение 3.По сигналу учителя ученики за партой меняются каточками, решают их и производят взаимопроверку. По второму сигналу учителя ученики 1 варианта остаются на месте, а ученики 2 варианта переходят за следующую парту и меняются карточкой с новым соседом и т.д.	Решают задания на карточках, проводят взаимопроверку, при необходимости корректируют своё решение или решение соседа.
Включение в систему знаний и повторение.	13 мин	Найди ошибку. 1) sin (3π/2 + α) = - sin α 2) tg (π + α) = - tgα 3) cos (π/3 + α) = sin α Теперь работаем с номером 25.3 стр.183 из учебника.	Ученики анализируют записи ищут ошибку. 1) sin (3π/2 + α) = - sin α 1) sin (3π/2 + α) = - cos α 2) tg (π + α) = - tgα 2) tg (π + α) = tgα 3) cos (π/3 + α) = sin α 3) cos (π/3 + α) = нет формулы приведения, так как к аргументу левой части добавляется π/3 Выполняют номер 25.3 из учебника у доски с подробным комментированием.
Рефлексия деятельности (итог урока)	6 мин	Урок подходит к концу. Запишите, пожалуйста, домашнее задание. Номера 25.2 и 25.4 на странице 183. Уберите тетрадки в портфель и пройдите с телефонов/ смартфонов тестирование https://forms.gle/cUqUrBPPPBKYcDhW7 После прохождения учащимися тестирования, учитель выводит диаграмму ответов на экран и анализирует с учениками результаты. Рефлексия «Корзина идей» Учащиеся записывают на листочках свое мнение об уроке, своей деятельности на уроке, интересных или сложных моментах. Все листочки кладутся в корзину (коробку, мешок), затем выборочно учителем зачитываются мнения и обсуждаются ответы. Учащиеся мнение на листочках высказывают анонимно.	Записывают домашнее задание. Проходят тестирование. По результатам тестирования делают вывод о том, достигли ли они цели урока. Рефлексируют свою деятельность на уроке.

---

---

Смотрите также файлы

• Фармацевтикалы технология кафедрасы.docx

• Особенности воспитания в семье ребёнка с проблемами речи. Всякое искусство и искусство воспитания тоже, имеет целью восполнить то, чего не достаёт от природы.docx

• Вертикальный дисплей.pdf

• Что является одной из частых причин заболевания поджелудочной железы.docx

• Построение umlмодели сапр. Диаграммы вариантов использования, классов.docx