Файл: Альтернативой и к нормативной в мировой практике все становится метод конечномоделирования железобетонных.docx
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 04.02.2024
Просмотров: 18
Скачиваний: 1
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
В процессе эксплуатации железобетонные конструкции подвергаются воздействию различных факторов окружающей среды: силовых, физических, химических, техногенных и т.д. Расчет долговечности и надежности конструкций должен учитывать динамику процессов протекающих в материале под действием агрессивных сред. Для этого должны быть определены основные характеристики сопротивления бетонов действию химически-активных веществ и определен механизм взаимодействия материала со средой.
Многочисленные экспериментальные данные свидетельствуют о том, что значения расчетно-конструктивных параметров конструкций, а так же величины внешних воздействий носят случайный характер, т.е. отклоняются от средних значений, обычно принимаемых в расчетах. Можно утверждать, что метод, достоверно отражающий работу конструкции, должен в большей степени базироваться на методах теории вероятности. Следовательно, наличие достоверных характеристик расчетно-параметров и окружающей среды необходимым условием вероятностного расчета Для более оценки долговечности и безопасности при расчет конструкций отражать их работу при действии нагрузки и среды, а же учитывать характер величин в расчете.
Согласно нормативной документации [2], элементы рассчитывают действие изгибающих продольных и сил, моментов и местное действие (местное сжатие, ). При этом в исходных расчетных определяющих связь на пряжениями и применяют трех- двухлинейную диаграммы яния бетона; строятся по из вестным прочностным и мационным характеристикам (сопротивлению сжатию и пре дельным деформациям при и растяжении, модулю упругости и ).
Альтернативой и к нормативной в мировой практике все становится метод конечно-моделирования железобетонных
Современные методы расчета конструкций при большое значение в с тем что многие технологические решения, «бесконтактные» арматурных конструкций (петлевых стыков, а же прямых гнутых перепусков с личными анкерными ), сдерживаются ввиду или неполноты -методической базы рас чета и этих конструкций. В с этим необходимым научно-обеспечение проектов конструкций зданий и АЭС для методов строительства с методов вычислительной
Расчет в том железобетонных, с
целью их безотказной, работы в эксплуатации. Задача достаточно сложная, как механические материала, размеры элементов, воздействия и являются случайными [4,3].
Поэтому расчетное условие записывать в неравенства: max R min S (1.1)
Smax – (предельное) усилия от воздействий в Rmin – значение усилия, сопротивление элемента. А
многочисленных экспериментальных [5, 3] что кривые распределения функций S и R нормальный характер. Тогда безотказной работы конструкций можно в виде
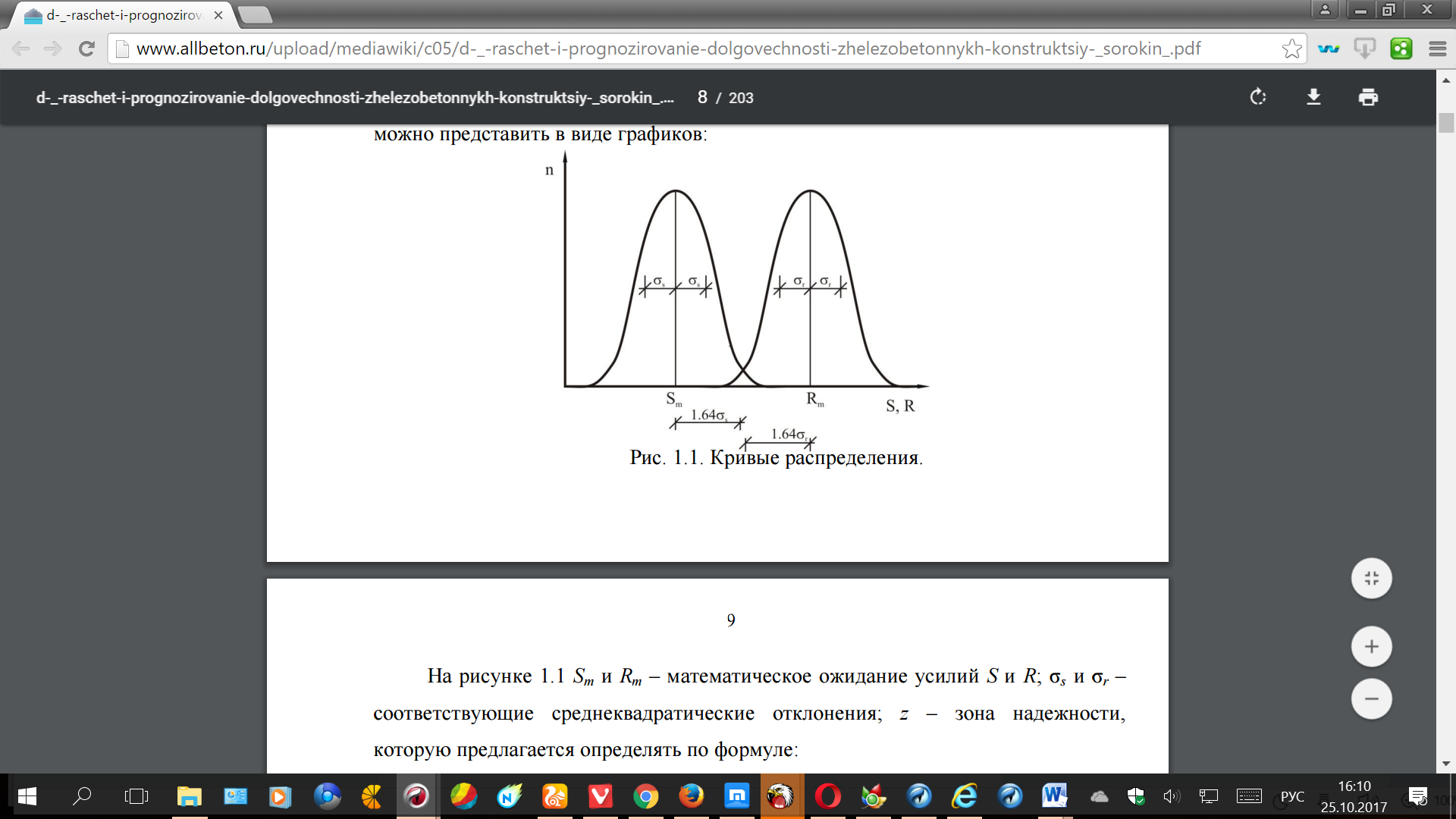
На 1.1 Sm и Rm – ожидание усилий S и R; и σr – среднеквадратические отклонения; z – надежности, предлагается определять формуле:
mn mn z R S (1.2)
Rmn и Smn – характеристические значения
Rmn Rm r 1.(1.3)
mn m s S S 1.64 (1.4)
Так распределение функций Rmn и Smn закону близкому к то распределение z будет нормальным.
Тогда вероятности безотказной элемента β определяться функцией
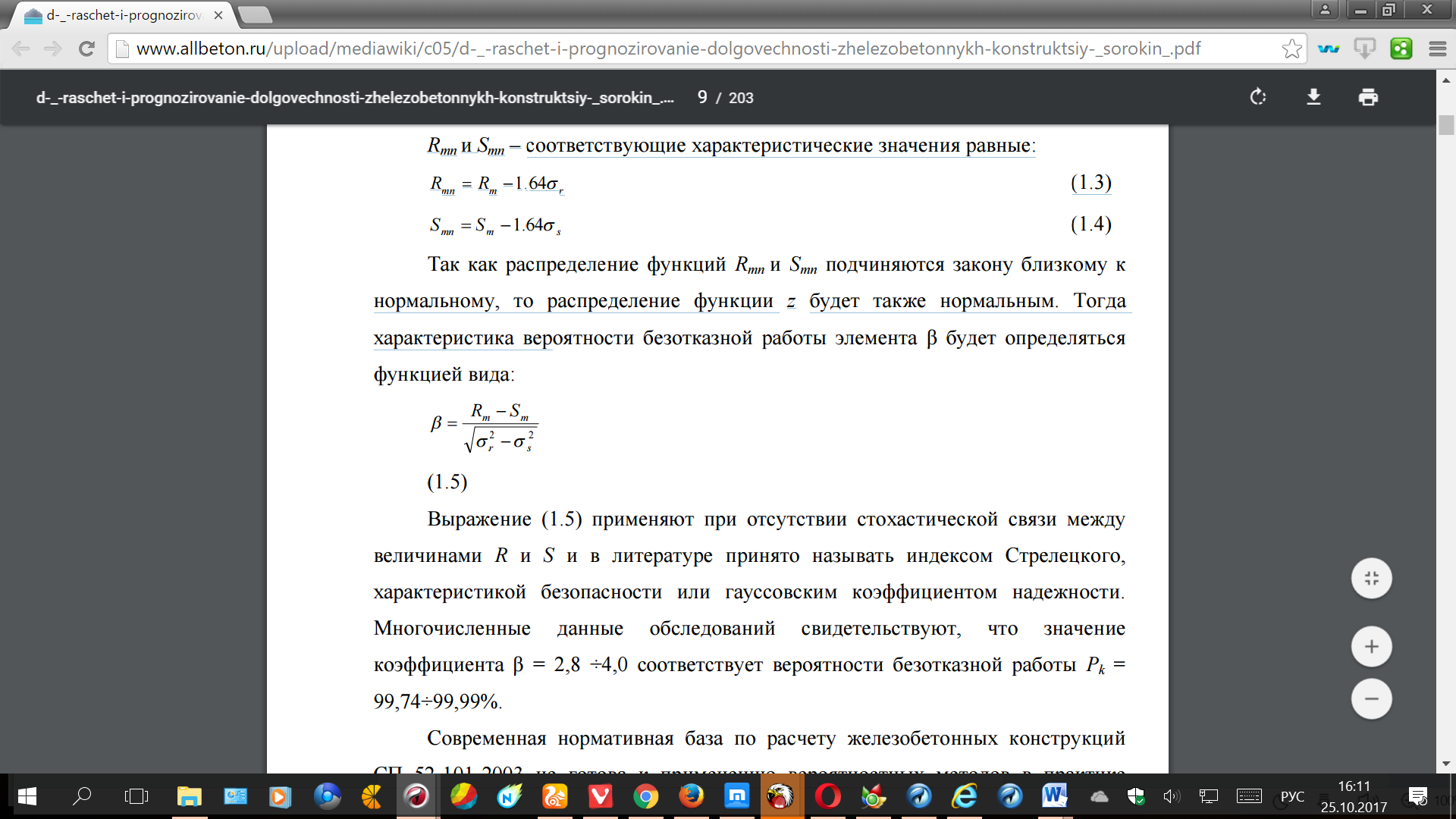
Выражение (1.5) при отсутствии связи между R и S и в принято называть Стрелецкого, безопасности или коэффициентом надежности. Многочисленные обследований свидетельствуют, значение коэффициента β = 2,8 ÷4,0 вероятности безотказной Pk = 99,74÷99,99%
Метод по разрушающим дает более представление о работе железобетона, более правильно прочностные и свойства материалов и в случаев позволяет более экономичные решения. Недостатком расчета по усилиям является единого коэффициента в связи с не могут явно учтены отклонения фактических нагрузок, характеристик материалов, сечений и пр. расчетных значений.
Кроме метод расчета разрушающим усилиям определять только способность конструкции. Основными метода расчета предельным состояниям прежних являются установление предельных конструкции и системы расчетных взамен общего запаса прочности.
Для надежности сооружений методы теории и математической [3]. Большая научных изысканий в области существующего метода [3]. Условно выделить следующие способ более обоснования существующих обеспечивающих надежность конструкции; расчета вероятности работы; существующих норм
Все надежности, могут быть при формулировании требований к конструкциям
, функции вероятности за какой-промежуток времени.
Условие математически выражается [56]: R - Q 0 (1.9) где R и Q – величины с законами распределения. Q – от внешних и других R – способность выраженная в же единицах.
Вопрос в способе вероятности отказа, учета изменения конструкций и во времени. Разработаны методы определения конструкций с вероятностного подхода и оценка.
Если способность R и от нагрузки Q по нормальному то интеграл (1.6) через интеграл P 1 - ( ) (1.11)
- надежности (безопасности);
В нелинейной функции 1 n g g x , x ..., x 2 , g=RQ – применить метод линеаризации, на разложении в Тейлора нелинейной в окрестности положения центра случайного вектора 1 n x , x ..., x 2 . Формула приближенного вычисления параметров нелинейной независимых случайных записывают в
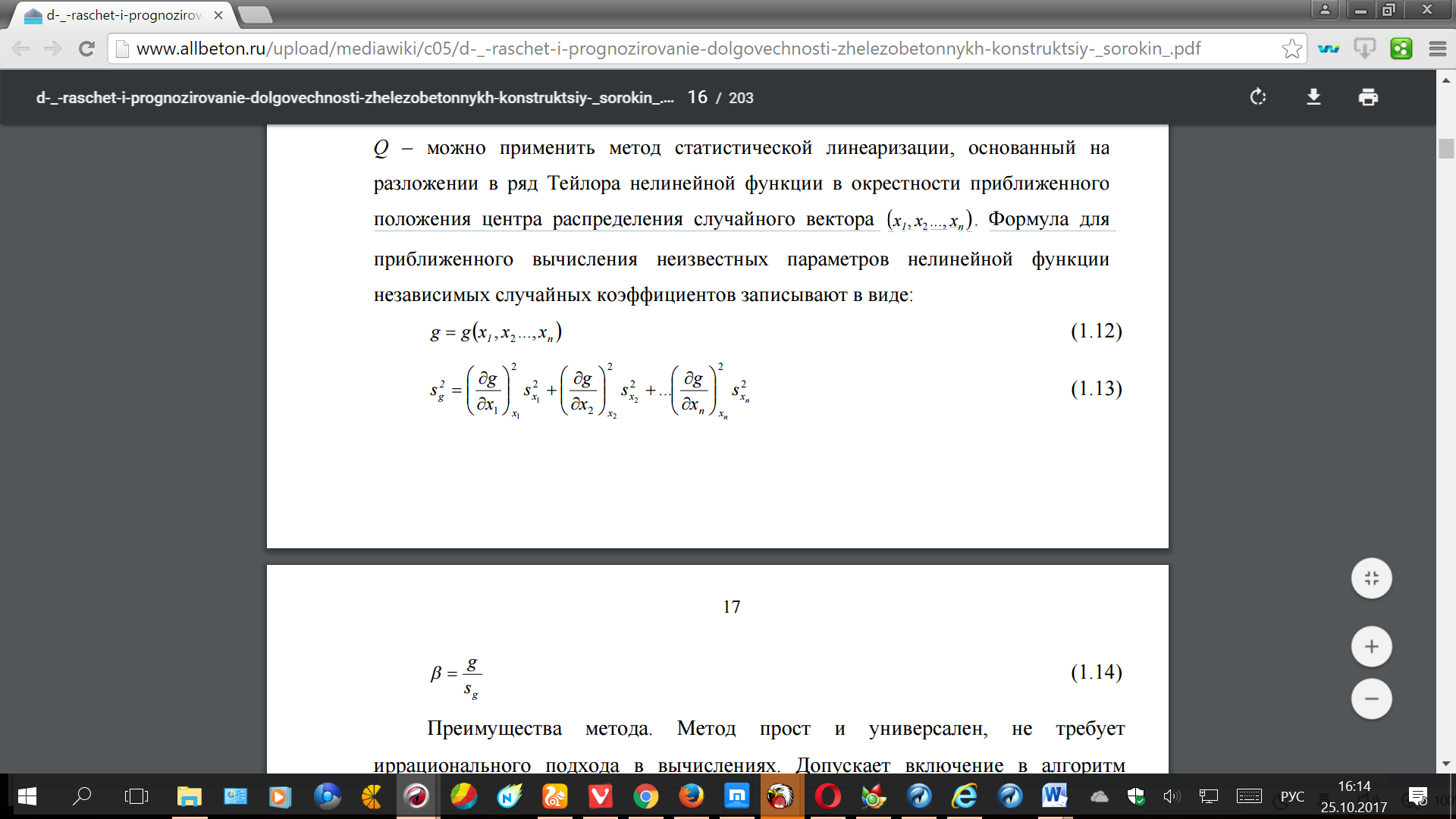
Если величины распределены по нормальному теоретически можно такое их чтобы привести распределение к (метод первого ). Однако, решение здесь только для производных от
В случаях преобразование собой аппроксимацию законов нормальным. Эта должна выполняться границе области (точка подгонки) с плотностью распределения величин, как в этой точки наиболее вероятные значения. Алгоритм основан на итерационном приближении точки подгонки тех пор, не окажется, аргумент функции безотказной работы индексу надежности. Что минимальную погрешность в
В создания конечно-модели, и анализа все геометрические конструкции и -механические свойства задаются параметри Это позволяет оптималь ные конструкции, армиро вания, бетона и исходя из работы и ответственности сооружений. Особый в этой представ ляло механизма разрушения, а общих закономерностей са трещинообразования с петлевыми
Полученные в численного расчета -деформированное со плит с армированием и образования трещин с экспериментальными а также некоторые из относящихся к разрушения подобных [2]. Расчетным было подтверждено о том, определяющим фактором, на не способность подобных следует считать радиально расположенных по контуру стыков, а первичных трещин нижней грани под областями на грузки, это случается простом продольном
При наблюдалось возникновение трещин в плоскости между петлевыми стыками. Кроме подтверждено предположение, наличие поперечной внутри петлевых (замковая арматура) влия ет несущую способность плит.
Установлено, наибольшие растягивающие в арматуре зованы в перехода прямолинейных нижнего ряда в окруж участки.
СПИСОК ЛИТЕРАТУРЫ
1. Карпенко Н.И. Общие механики железобетона. М.: Стройиздат, 416 с.
2. ANSYS Help. ANSYS, Inc. http://www. ansys.com/Support/Documentation,
3. LS-DYNA User’s Keyword Manual. Livermore Software Technology Corporation, http://www.lstc.com/download/manuals,
4. ABAQUS Analysis User’s Manual, Vol. III – Materials. Dassault Systems, http://www.3ds.com/ support/documentation/users-guide, 2013.
5. Ишлинский А.Ю., Ивлев Д.Д. Математическая теория пластичности. М.: Физматлит, 2014. 702 с.
6. Brannon R.M., Leelavanichkul S. Survey of Four Damage Models for Concrete// Sandia National Laboratories. http://prod.sandia.gov/ techlib/access-control.cgi/2009/095544.pdf, 2015.