Контрольная работа по дисциплине «Финансовый менеджмент»выполнена по методике Красиной Ф.А.Вариант 2Задание 1. Клиент поместил в банк 100 тыс. руб. под простую процентную ставку 11% годовых. Какая сумма будет на его счете через а) 7 месяцев; б) три года; в) 4 года 3 месяца? При расчете используйте формулу обычного процента с приближенным числом дней.Решение: Для решения задачи используем формулу F = P(1 + n*r), гдеF – наращенная сумма,Р – вложенная сумма, n – количество лет, r – простая процентная ставка. а) при P = 100 000, n = 0,58, r = 11, получаем:F = 100 000(1+0,58*0,11) = 106 380 руб. б) при P = 100 000, n = 3, r = 11, получаем: F = 100 000(1+3*0,11) = 133 000 руб. в) при P = 100 000, n = 4,25, r = 11, получаем: F = 100 000(1+4,25*0,11) = 146 750 руб.Задание 2. Предприниматель получил ссуду в 600 тыс. руб. на полгода. Банк предоставляет ссуду на условиях начисления простых учетных процентов по ставке 16 % годовых. Какую сумму предприниматель будет должен банку?Решение: Для решения задачи используем формулу F = P(1 + r*t/T), гдеt – продолжительность финансовой операции в днях;Т – количество дней в году. При Р = 600 000, Т = 360 дн., r = 16, t = 6*30 = 180 дн., получаем:F = 600 000(1+0,16*180/360) = 648 000 руб. Задание 3. В банк вложены деньги в сумме 800 тыс. руб. на полтора года под 10 % годовых с ежеквартальным начислением сложных процентов. Определите доход клиента в этой финансовой операции.Решение: Для решения задачи используем формулу F = P(1 + r)ⁿ. При Р = 800 000, r = 10, n = 18/12 = 1,5, получаем:F = 800 000(1 + 0,1)^1,5 = 800 000 * 1,154 = 923 200 руб.923 200 – 800 000 = 123 200 руб.Задание 4. Определите дисконтированную сумму при учете 100 тыс. руб. по простой и сложной учетной ставкам, если годовая ставка равна 18 % годовых и учет происходит за 30 дней, 180 дней, 1 год, 3 года, 5 лет. Полагать год равным 360 дням.

---

Решение: Для решения задачи используем формулы:Р = F(1 – n*d) – для простой учетной ставки;Р = F(1 – d)ⁿ – для сложной учетной ставки. При F = 100 000, d = 0,18 и различных n, получаем:

Способ дисконтирования	30 дней	180 дней	1 год	3 года	5 лет
Простая ставка	0,985	0,91	0,82	0,46	0,1
Сложная ставка	0,984	0,905	0,82	0,551	0,371

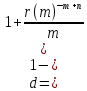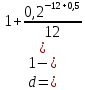
Задание 5. Банк выдает ссуду под сложную процентную ставку 20 % годовых. 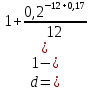Какую простую годовую процентную ставку должен установить банк, чтобы его доход не изменился, если начисление процентов происходит а) по полугодиям; б) каждые 2 месяца; в) каждую неделю.Решение:Для решения задачи используем формулу , приа) n = 0,5 получаем следовательно, простая учетная ставка составит 22,41 % годовых.б) n = 0,17 получаемследовательно, простая учетная ставка составит 23,29 % годовых.в) n = 0,02 получаем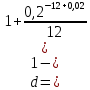следовательно, простая учетная ставка составит 23,71 % годовых.Задание 6. Контракт на выплату 10 000 долл. 1 ноября и выплату 5 000 долл. 1 января следующего года необходимо заменить новым контрактом, в соответствии с которым 1 декабря выплачивается 6 000 долл., оставшаяся сумма погашается 1 марта. Определите сумму второго платежа на основе простой ссудной ставки (следующий год не високосный).Решение:

---

Применим простые процентные ставки. Запишем уравнение эквивалентности: 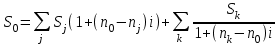,где S_j - размеры объединяемых платежей со сроками n_j < n₀; S_k - размеры платежей со сроками n_k > n₀ .За базовую дату, то есть за дату приведения, примем 01.01 (0-й день или 365-й день).01.10 – 274-й порядковый день в году; 01.01 – 365-й или 1 день в новом году; 01.12 – 335-й день в году;01.03 – 60-й день.Получаем: 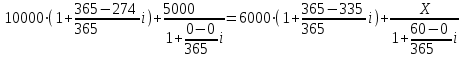.Определим Х. Примем условно ставку процента равную 10%: 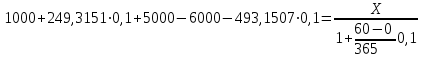; 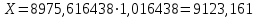.Сумма оставшегося платежа составляет 9123,161 долл. Задание 7. Номинальная процентная ставка, компенсирующая при наращении инфляцию, составляет 48 % годовых. Определите инфляцию за квартал, если начисление сложных процентов осуществляется каждый месяц.Решение: Приравняем годовой индекс инфляции к множителю наращения за год. Полагая r¹² = 0,48, получаем:I_p¹ = (1 + r¹²/12)¹² = (1 + 0,48/12)¹² = 1,601.Следовательно, индекс инфляции за квартал составит:I_p^0,25 = 1,601^0,25 = 1,1249.Значит темп инфляции за квартал равен в среднем 12,49 %. Задание 8. Анализируются два накопления денежных средств по схеме аннуитета пренумерандо: 1) класть на депозит 200 тыс. руб. каждые полгода при условии, что банк начисляет сложные проценты по ставке 8 % с ежеквартальным начислением процентов; 2) делать ежегодный вклад в размере 420 тыс. руб. при условии, что банк начисляет сложные проценты по ставке 7 % с ежемесячным начислением процентов. Какая сумма будет на счете через 5 лет при реализации каждого плана?Решение:Используем формулу: 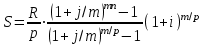, где 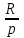- размер вклада; р – число вкладов в году; j – ставка процента; m – число периодов начисления.Получаем:- в случае 1:

---

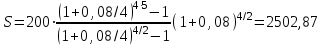
тыс. руб.;

- в случае 2: 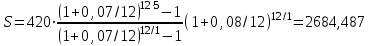тыс. руб.

В первом случае сумма составит 2502,87 тыс. руб., а во втором – 2684,487 тыс. руб.

Задание 9. По условиям контракта на счет в банке в начале года в течение 6 лет поступают платежи. Первый платеж равен 50 тыс. руб., а каждый последующий по отношению к предыдущему увеличивается на 2 %. Оцените этот контракт, если банк начисляет по вкладам сложные проценты из расчета 9 % годовых.

Решение:

Ежегодный платеж увеличивается в 1,02 раза (2 %), значит денежный поток представляет собой переменный аннуитет постнумерандо с постоянным относительным изменением его членов. Поэтому для оценки аннуитета воспользуемся формулой: FV_pre = FV_pst(1 + r), полагая А = 50 000, n = 6, q = 1,02 и r = 0,09, получаем:


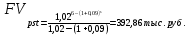
FV_pre = 392,86 · (1 + 0,09) = 428,22 тыс. руб.


Задание 10. Финансовая компания в соответствии со своими обязательствами должна выплачивать вкладчикам по 15 млн. руб. ежегодно в течение десяти лет. Какой суммой должна располагать компания, чтобы иметь возможность выполнить обязательства, если норма доходности составляет 10 % за год и выплаты происходят постоянно и достаточно равномерно?

Решение:

Используем формулу аннуитета постнумерандо, определим современную сумму, необходимую для выплат:

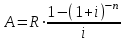, где R – ежегодная выплата; i – ставка процента; n – число лет.

Получаем:

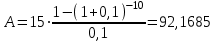млн. руб.

Необходимая сумма должна составить 92,1685 млн. руб.

Задание 11. Компания за предыдущий год выплатила 1 тыс. руб. за акцию. Согласно прогнозам дивиденды по акциям этой компании будут расти на 50 руб. ежегодно в течение неопределенно долгого времени. Сделайте вывод о целесообразности покупки акций компании по цене 21 тыс. руб., если можно поместить деньги в банк на депозит под 10 % годовых.

Решение:

Так как темп рост дивидендов со временем изменятся, то правильным решением в данном случае будет использование следующей формулы:



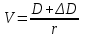
где D₀– дивиденд на акцию в момент времени t;

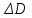– предполагаемый прирост дивидендов;

r – норма доходности.

Получаем:

---

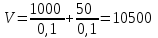
руб.

Покупка акции по цене 21 тыс. руб. нецелесообразна, так как текущая цена акции составляет 10,5 тыс. руб., следовательно, выгоднее положить деньги в банк.

Задание 12. Годовой спрос на продукцию составляет 15 000 единиц. Стоимость заказа равна 1500 рублей за заказ. Издержки хранения одной единицы продукции равны 4500 руб. в год. Время доставки заказа 6 дней. Определить оптимальный размер заказа, общие издержки по запасам, уровень повторного заказа. Количество рабочих дней в году принять равным 300.

Решение:

Оптимальный размер заказа рассчитаем по формуле:

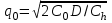, где

D - ежегодный спрос на запас продукции;

С₀ - переменная стоимость подачи одного заказа;

C_h - переменная стоимость хранения единицы продукции в запасе.

Получаем:

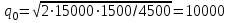ед.

Общие издержки по запасам рассчитаем по формуле:

ТС = С₀ (D/q) + C_h(q/2).

Получаем:

ТС=1500·15000/10000+4500·10000/2=22502250 руб.

Рассчитаем уровень   повторного   заказа  по формуле:

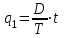, где

Т – количество рабочих дней в году;

t – время доставки заказа.

Получаем:

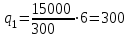ед.

Можно сделать вывод, что оптимальный размер запаса равен 10000 единиц, общие издержки – 22502250 руб., а размер повторного запаса равен 300 ед.

Задача 13. Предприниматель планирует открыть свое предприятие 1 января 200_ года, инвестируя в него 3 000 долл. Он предполагает купить за 4 000 долл. Газель для перевозки овощей в магазины. Гараж для газели будет взят в аренду на условиях 500 долл. в квартал, которые будут выплачиваться авансом. Для оборудования гаража и газели потребуются дополнительные затраты в сумме 2 500 долл. Предполагается, что выручка от реализации овощей в ближайшие полгода составит 30 000 долл. и будет равномерно распределена в этом периоде. Торговая надбавка над закупочной ценой овощей составит 30 %. Овощи будут закупаться и реализовываться еженедельно за наличные. Для начала деятельности необходимы оборотные средства в размере 500 долл. Текущие ежемесячные расходы составят:

- заработная плата помощника – 300 долл. (включая все налоги);

---

Смотрите также файлы

• араанды облысы білім басармасыны Саран аласыны білім бліміні 7 мектепинтернаты кмм жазы мектеп сабатарына атысу журналы.docx

• Курс таырыбы Апаратты объектілерді ру жне трлендіру Саба таырыбы.docx

• Акт пні бойынша 4сыныпа арналан ЫСа мерзімді жоспарлар жинаЫ.docx

• Время на выполнение задания в подгруппах 2025 минут.docx

• Лекция 12. Гносеология учение о познании. Соотношение абсолютной и относительной истины.docx