ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 04.02.2024
Просмотров: 42
Скачиваний: 2
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
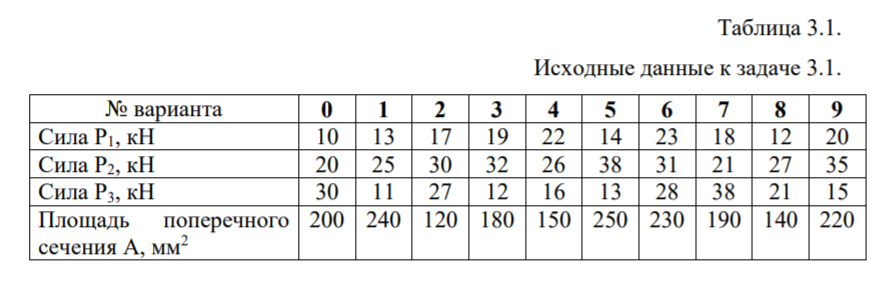
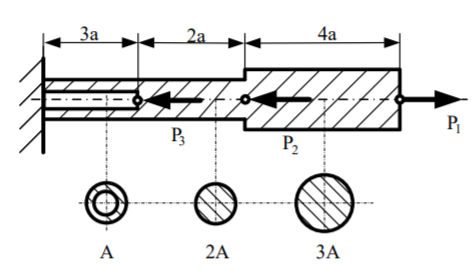
Дано:
Р1=10кН;
Р2=21кН;
Р3=11кН;
А=120мм2;
Е=2∙105Мпа;
[∆l]=3∙10-4м;
[σ]=160Мпа;
а=2м.
Найти: Реакцию опоры, продольное напряжение и удлинение на каждом участке стержня.
Решение:
1. Строим расчетную схему стержня.
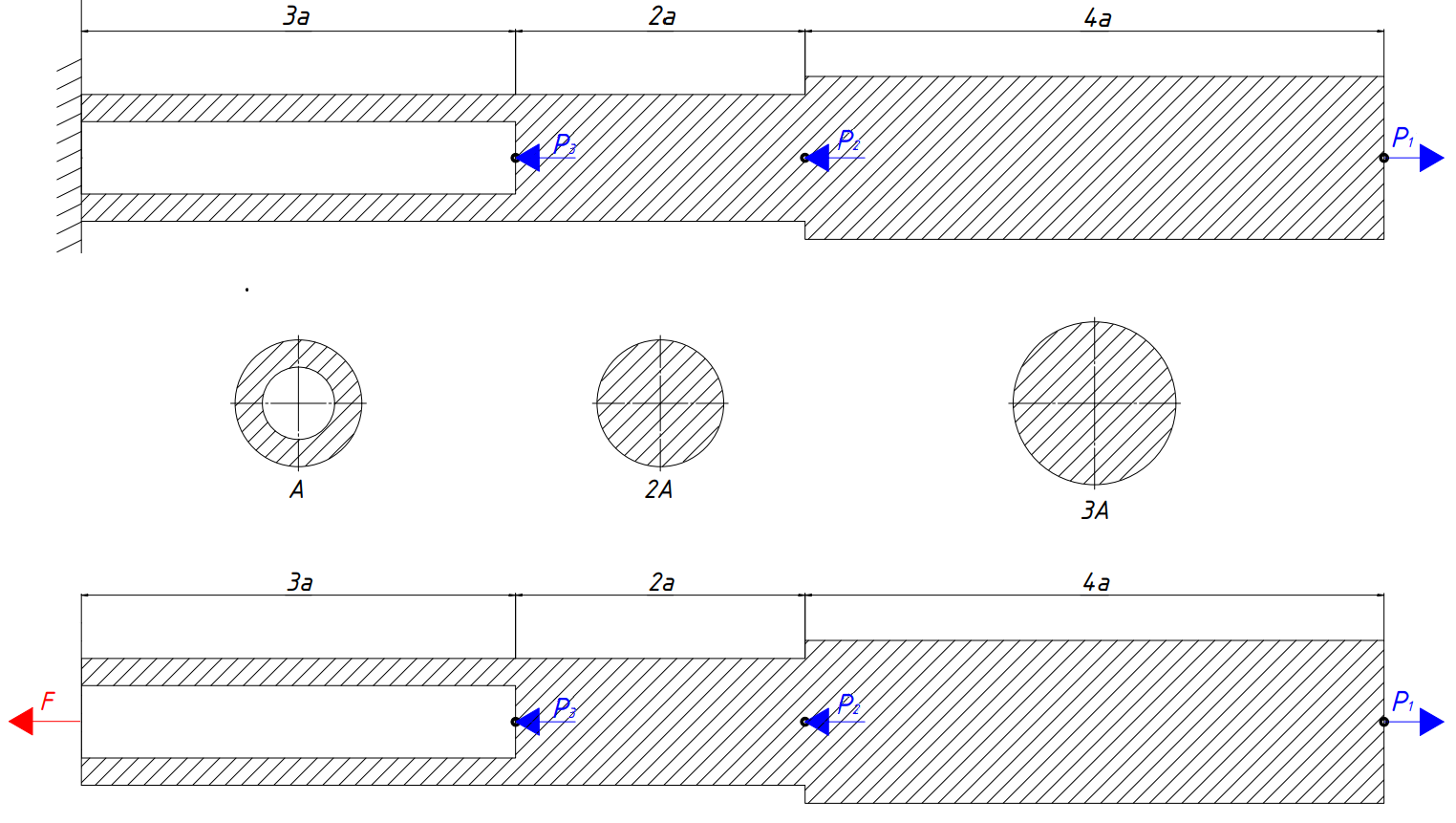
Рис. 1 – Расчетная схема стержня.
2. Определяем опорную реакцию стержня.
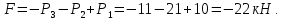
3. Определяем значения продольных сил, разбив стержень на участки в характерных сечениях.
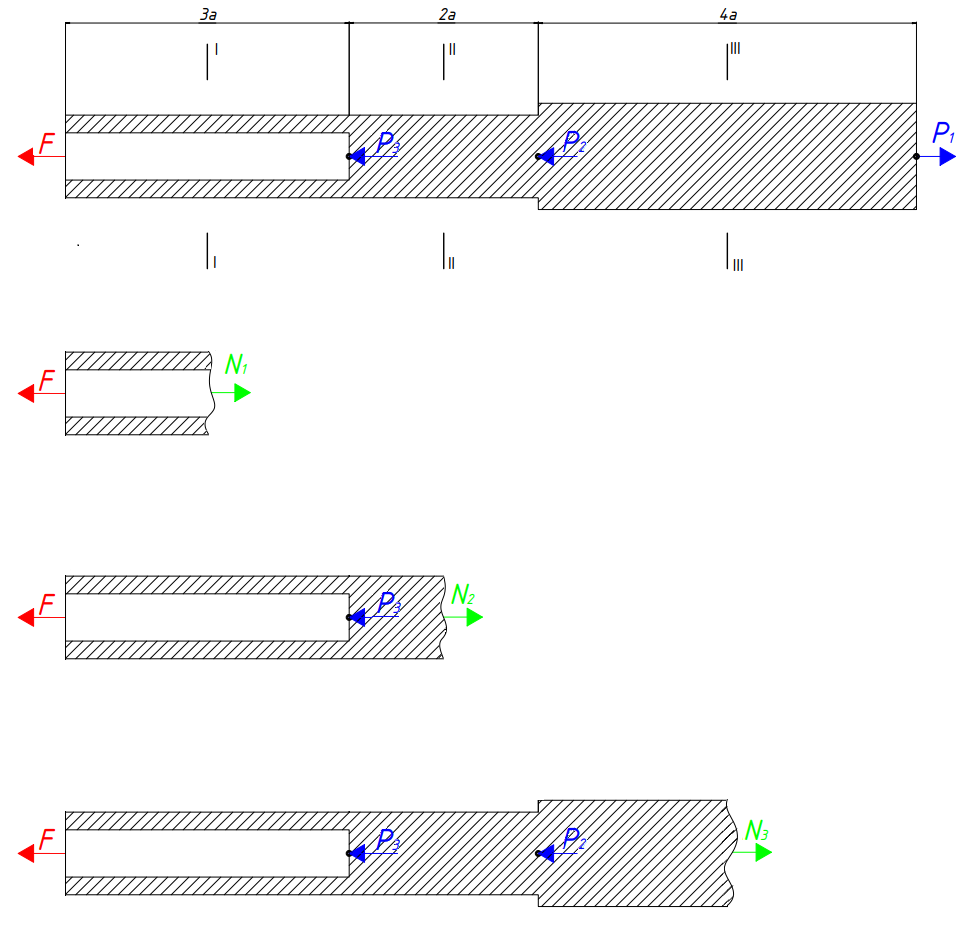
Рис. 2 – Метод сечений
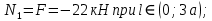
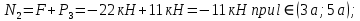
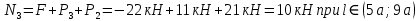.4. Определяем по формулам нормальные напряжения на характерных сечениях.
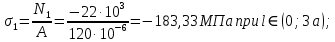
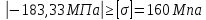,условие не выполняется, следовательно, подберем площадь сечения данного участка:
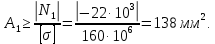
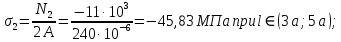
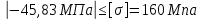, условие выполняется.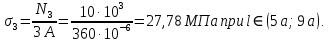
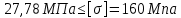, условие выполняется.5. Для определения перемещений отдельных сечений стержня вычисляем абсолютные деформации отдельных его участков:
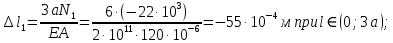
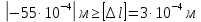
условие не выполняется, следовательно, подберем площадь сечения данного участка из условия абсолютного удлинения:
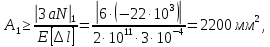
Принимаем площадь сечения участка
.
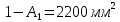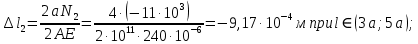
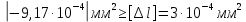
условие не выполняется, следовательно, подберем площадь сечения данного участка из условия абсолютного удлинения:
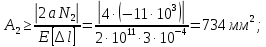
Принимаем площадь сечения участка
.
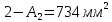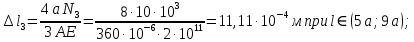
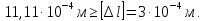
условие не выполняется, следовательно, подберем площадь сечения данного участка из условия абсолютного удлинения:
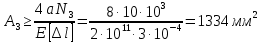;Принимаем площадь сечения участка
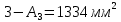.6. Определяем перемещения характерных сечений стержня.
Перемещения характерных сечений стержня находим суммирование абсолютных деформаций отдельных участков стержня:
,
,
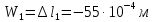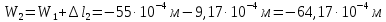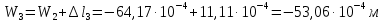.По результатам этих расчетов строим эпюры продольных сил, нормальных напряжений и перемещений.
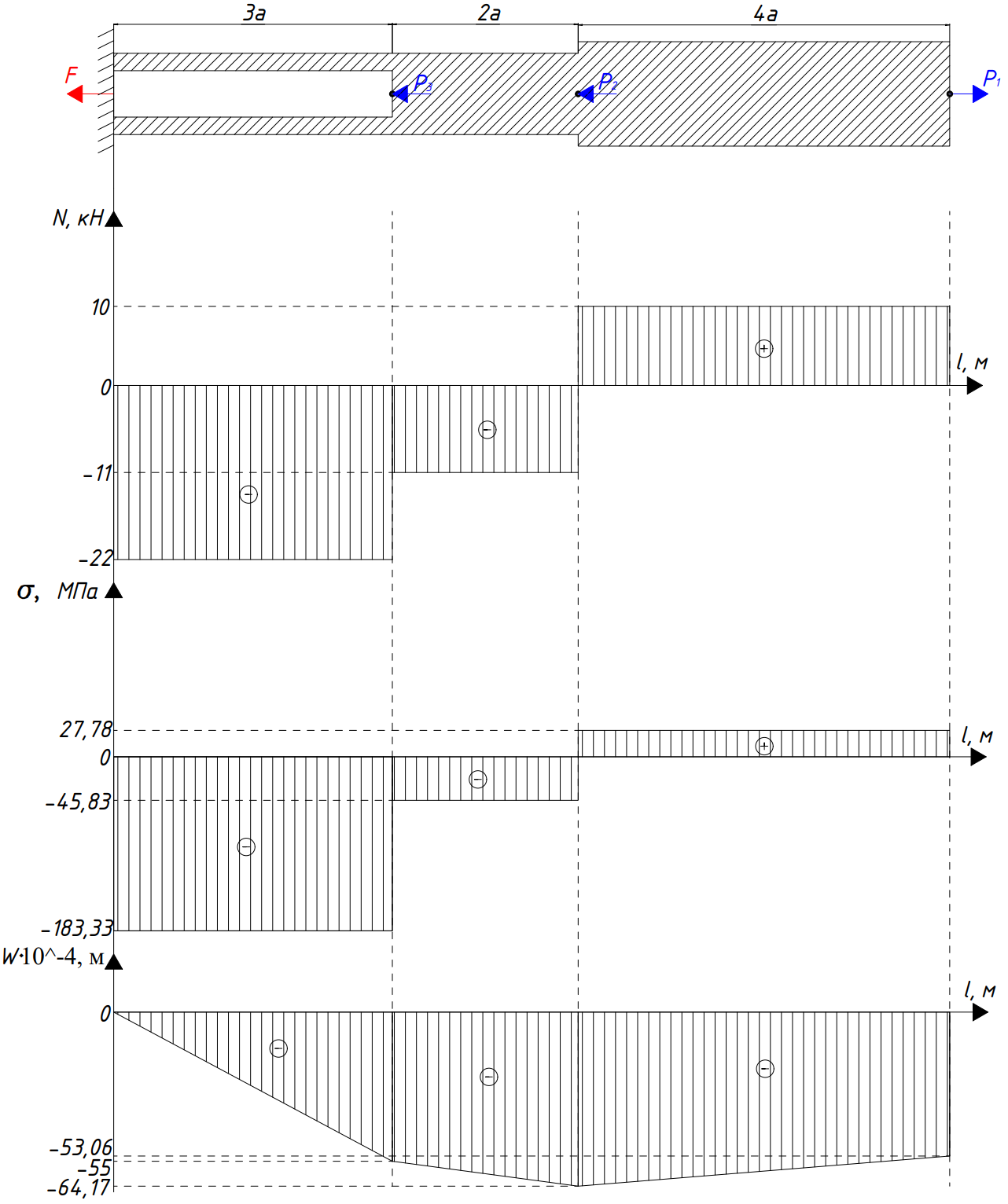
Рис. 3 – Эпюры продольных сил, нормальных напряжений и перемещений.
Задача 2.
Дано:
М1=16кНм;
М3=21кНм;
М2=31кНм;
М4=22кНм;
d=h=24мм;
d/D=0,55 (D=44мм);
h/b=1 (b=24мм);
а=2м;
G=8∙104МПа.
Найти: крутящие моменты, касательные напряжения и абсолютные углы закручивания на каждом участке вала.
Решение:
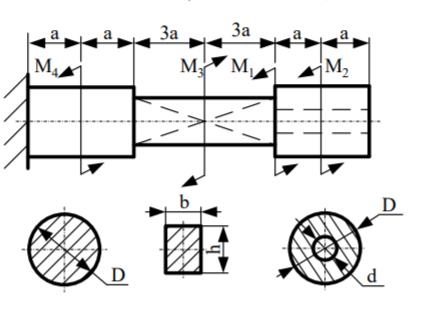
1. Составляем расчетную схему вала.
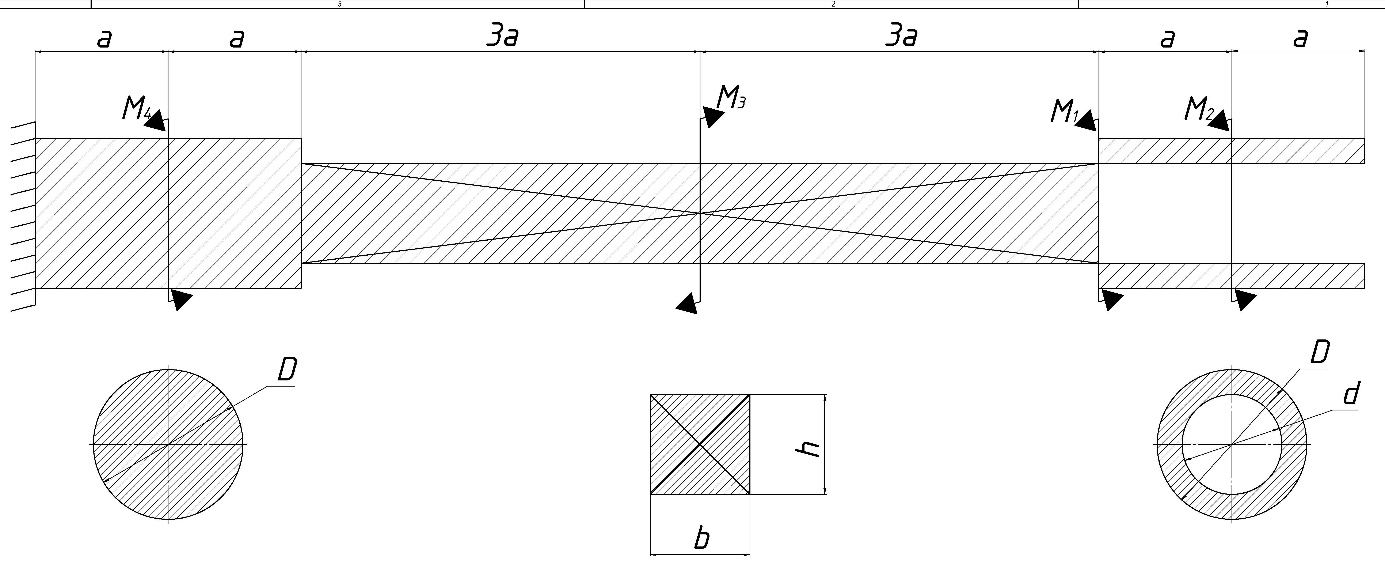
Рис 5. – Схема вала.
Определим методом сечений значения крутящих моментов на каждом силовом участке от свободного конца вала. Крутящий момент
равен алгебраической сумме внешних моментов, действующих на вал по одну сторону сечения.
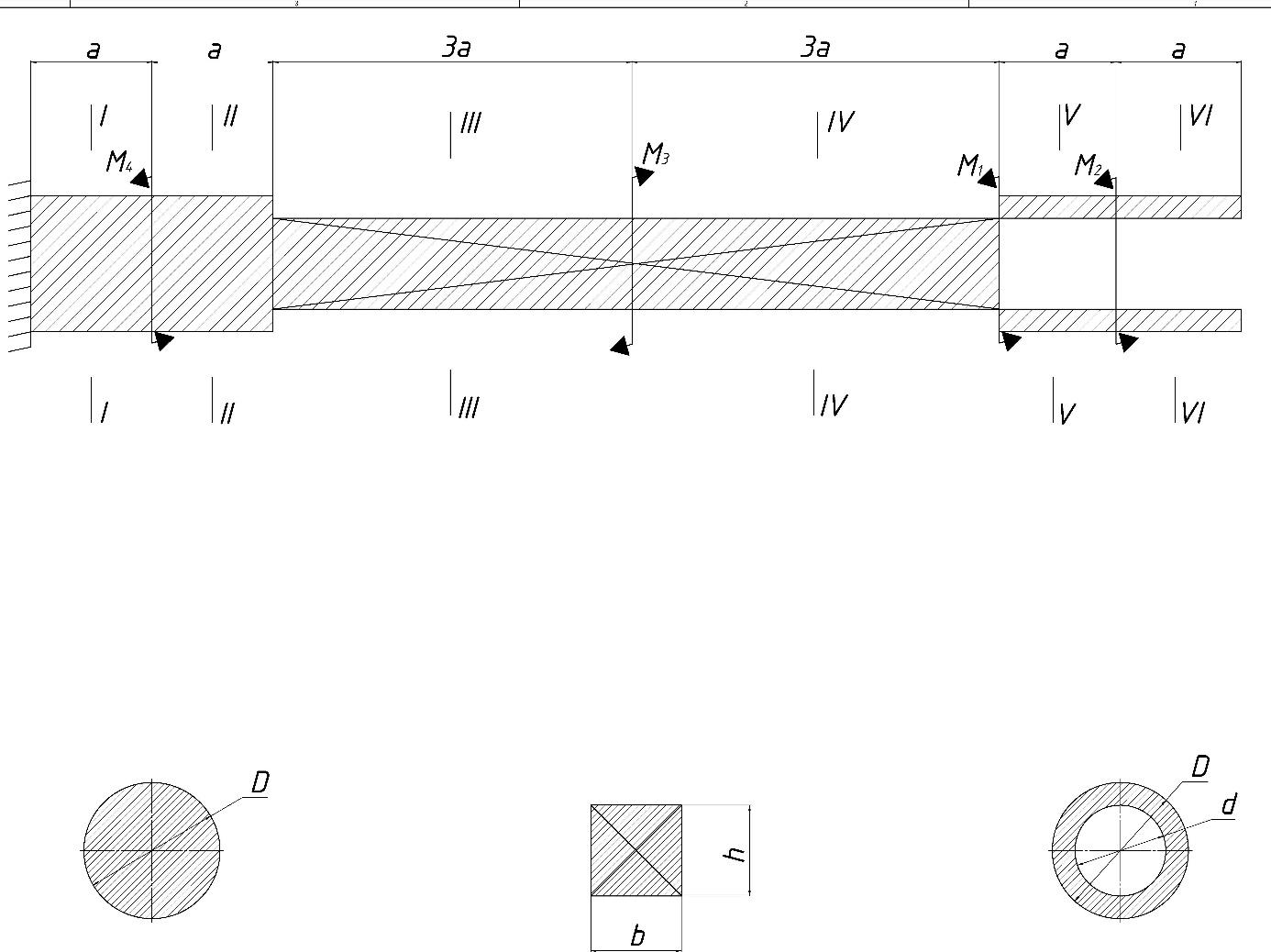
Рис. 6 – Метод сечений.
2. Определяем крутящий момент на каждом участке.
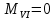при l∈ (0; а);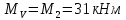
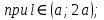
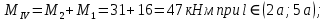
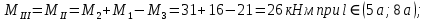
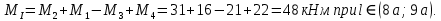
3. Определяем касательных напряжений.
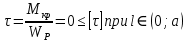
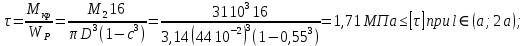
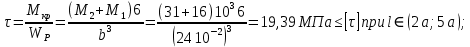
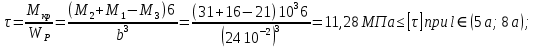
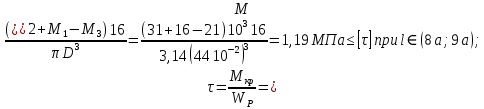
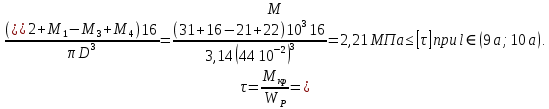
4. Определяем угла поворота участка вала.
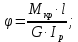
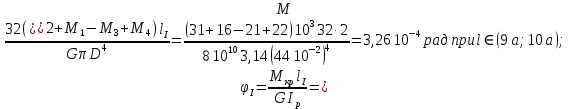
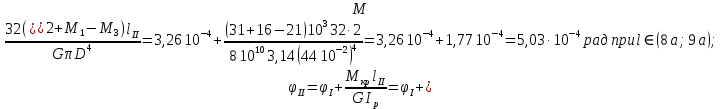
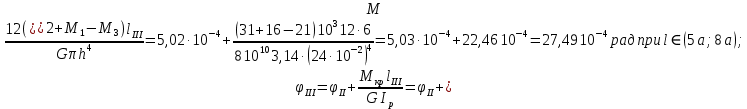
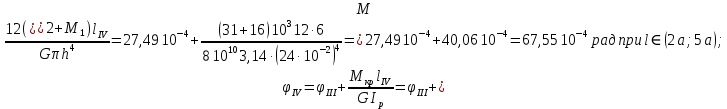
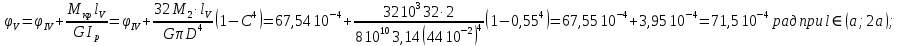
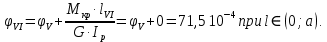
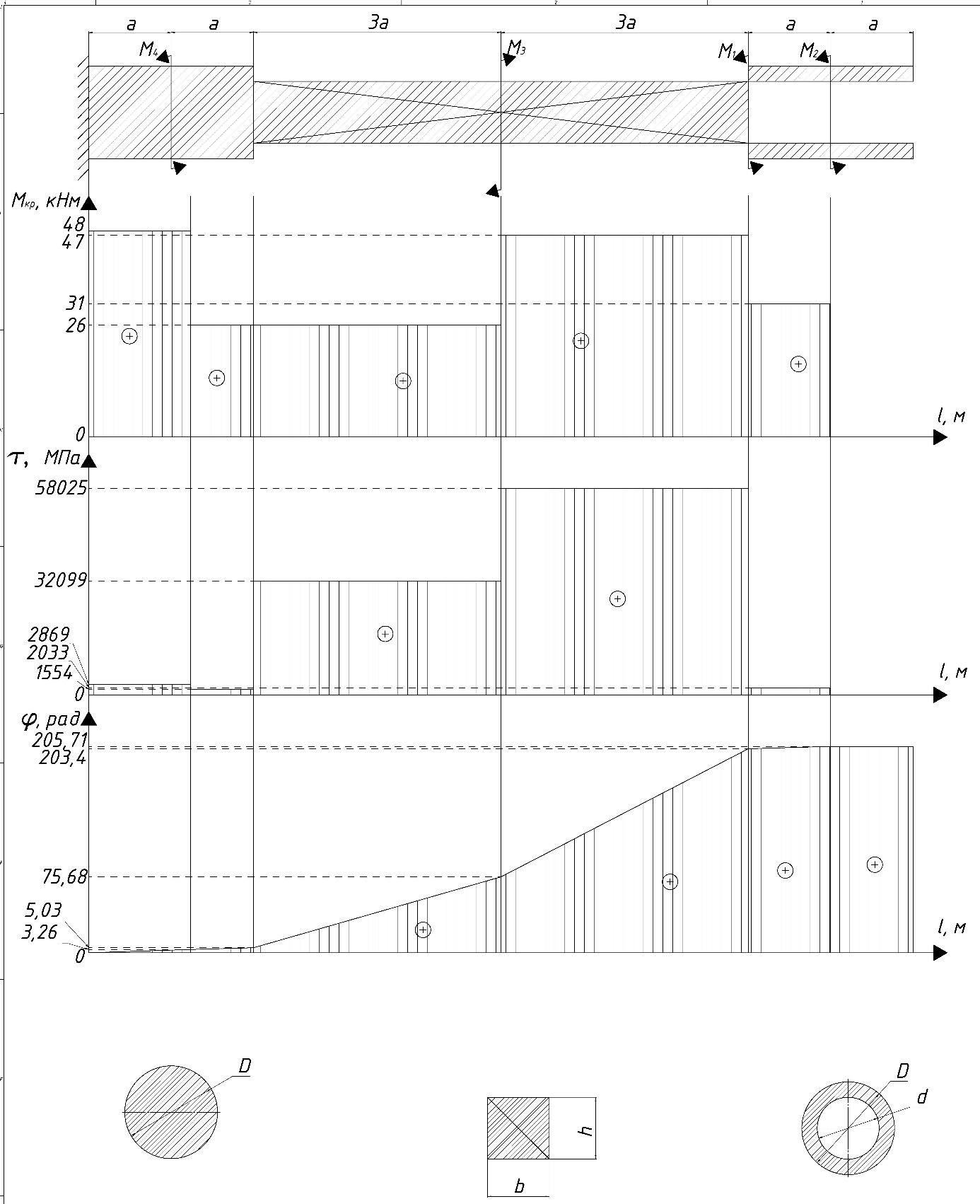
Рис. 7 – Эпюры крутящих моментов касательных напряжений и углов закручивания.
Задача 3.
Дано:
М=16кНм;
Р1=25кН;
Р2=60кН;
q=10кН/м;
а=2м.
Найти: силу реакции в опоре, поперечные силы и изгибающие моменты на каждом участке стержня, размеры для двутаврового и круглого поперечного сечения.
Решение:
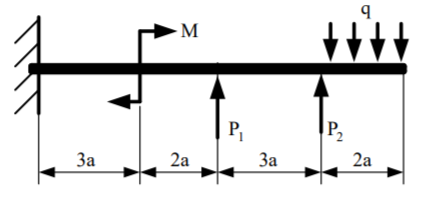
1. Составляем расчетную схему балки.
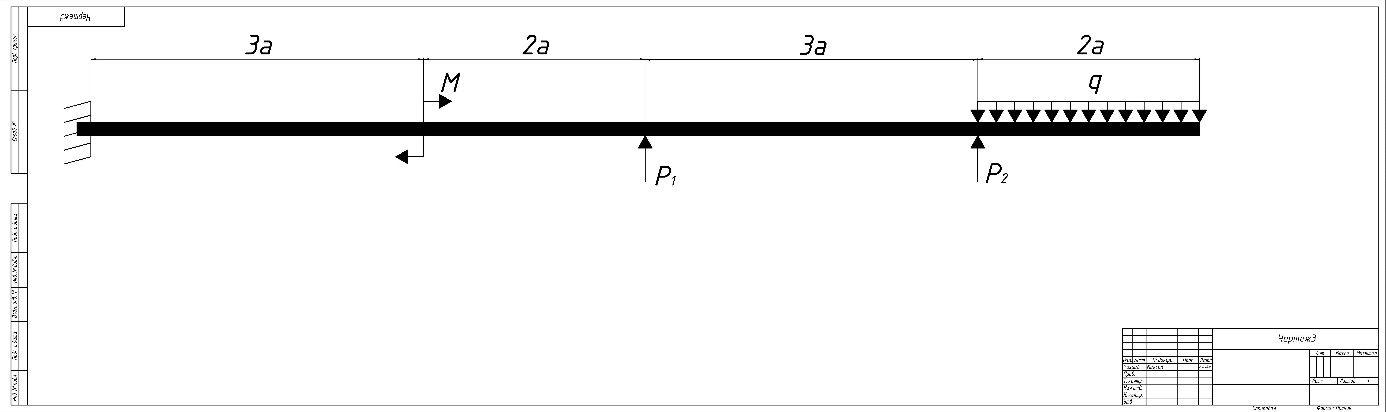
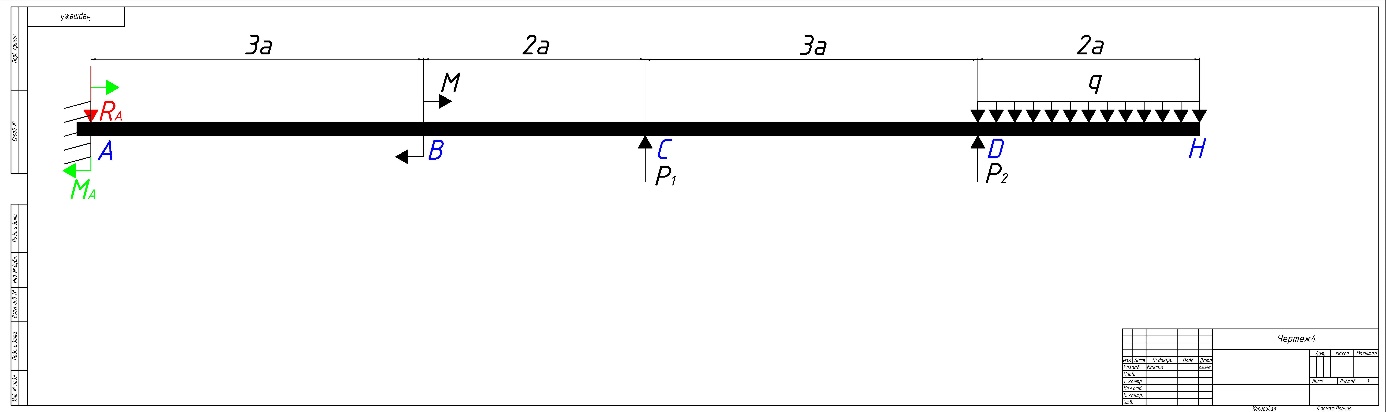
Рис. 8 – Схема балки.
2. Определяем величину и направление опорных реакций балки.
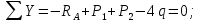
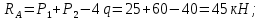
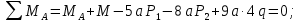
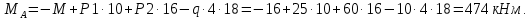
3. Определяем величины поперечной силы Q и изгибающего момента M по участкам балки методом сечений.
Участок АВ:
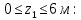
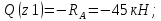
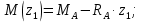
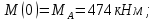
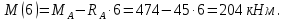
Участок ВС:
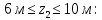
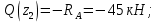
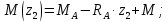
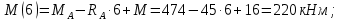
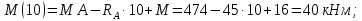
Участок CD:
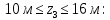
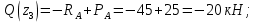
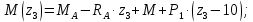
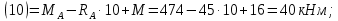
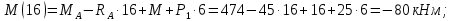
Участок DH:
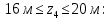
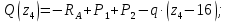
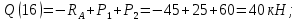
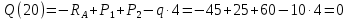
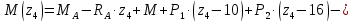
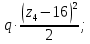
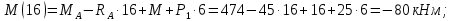
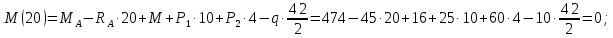
В середине участка DH:
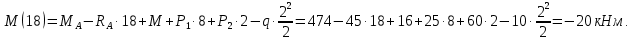
По полученным данным построим эпюры.
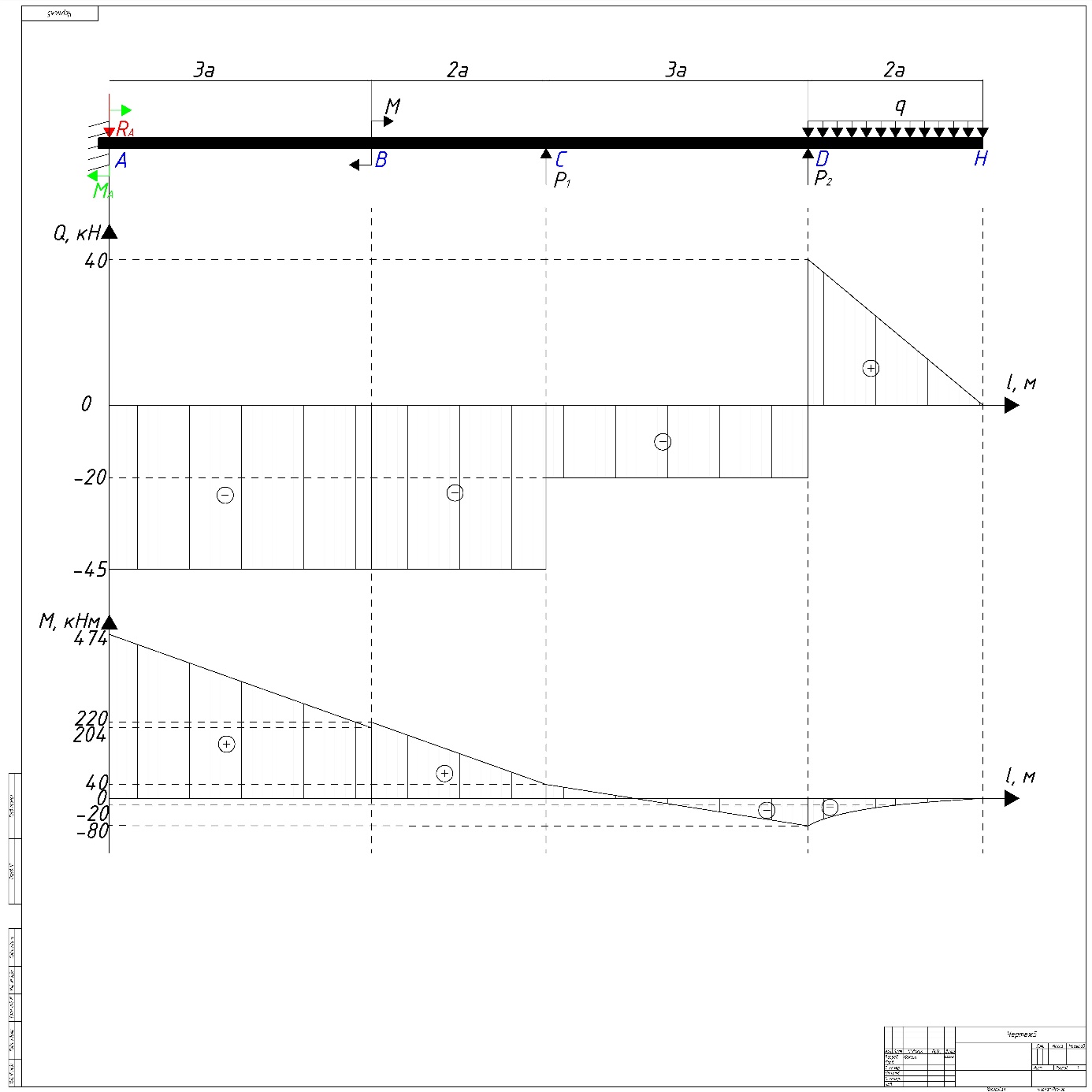
Рис. 9 – Эпюры поперечных сил и изгибающих моментов.
4. Рассчитаем размеры сечений
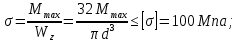
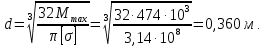
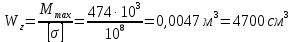
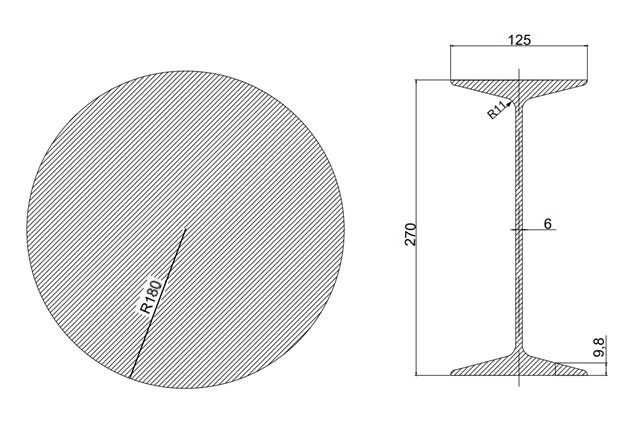
Рис. 10 – Сечения балки.