Файл: Metod_stat_1.doc

де n- кількість спостережень.

Параметри a іb можна розв’язати,використовуючи формули:

,.

Обчислений коефіцієнт регресії показує, що при збільшені розміру затрат на 1 га на 1 грн урожайність культури збільшується на­­­­­­­­­­­­­­­­­­­­________

Підставивши в рівняння знайдені параметри і фактичні значення факторної ознаки, дістанемо теоретичні рівні врожайності культури.

Якщо, то параметри рівняння визначенні правильно.

Таблиця 1

Вихідні та розрахункові дані для обчислення кореляційного рівняння зв’язку та

визначення коефіцієнта кореляції

Коефіцієнт кореляції визначається за формулою:

де r - коефіцієнт кореляції;

x -середня величина факторної ознаки;

y -середня ознака результативної ознаки;

xy -середня величина з добутку ознак та;

-середнє квадратичне відхилення факторної ознаки;

-середнє квадратичне відхилення результативної ознаки.

Коефіцієнт детермінації:

%

Висновок: Розрахунковий коефіцієнт кореляції свідчить про те, що між показниками врожайності та розміром затрат на 1 га існує в даному випадку __________, _________ зв’язок.

Завдання 2. На основі вихідних даних побудувати кореляційне поле, розв’язати рівняння зв’язку при криволінійній залежності між ознаками. Визначити кореляційне відношення, одержанні результати проаналізувати, а також визначити вірогідність кореляційного відношення.

Методика виконання

1. Якщо криволінійна залежність має форму параболи другого порядку, зв’язок між результативною і факторною ознакою виражають таким рівнянням:

,

де– теоретичні значення результативної ознаки;

x - значення факторної ознаки;

a,b,c-параметри рівняння.

Складають систему рівнянь:

Для спрощення розв’язку,замість значеньx вводять відхилення від середньої. Рівняння буде мати такий вигляд:

,

а система рівнянь:

Оскільки використовуючи спосіб найменших квадратів ми маємо , які дорівнюють нулю, то система рівнянь спрощується:

Середнє значення факторної ознаки за формулою:

.

Підставимо табличне значення в систему рівнянь.З другого рівняння визначимо параметрb. Перше і третє рівняння розділимо на коефіцієнти приa. В першому рівнянні наn, в третьому .З більшого рівняння віднімемо менше , визначимо параметрc.Підставивши в одне з попередніх рівнянь значення параметраc, визначимоa.

Підставивши в рівняння відповідні значення відхилень та їх квадрати, обчислимо теоретичні рівні результативної ознаки.

Таблиця 2

Вихідні та розрахункові дані для визначення параметрів рівняння параболи

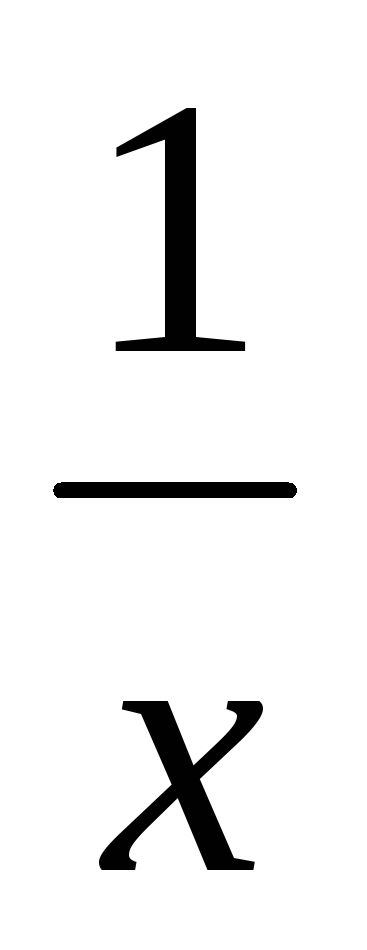
2. Якщо криволінійна зеленість між результативною і факторною ознакою має гіперболічний характер, розв’язуємо рівняння гіперболи:

,

де – теоретичне значення результативної ознаки;

x -значення факторної ознаки.

a i bПараметри рівняння регресії.

Для визначення параметрів а і в способом найменших квадратів складають систему рівнянь:

.

Таблиця 3

Вихідні та розрахункові дані для визначення рівняння гіперболи

Шифр підприємств	y	x
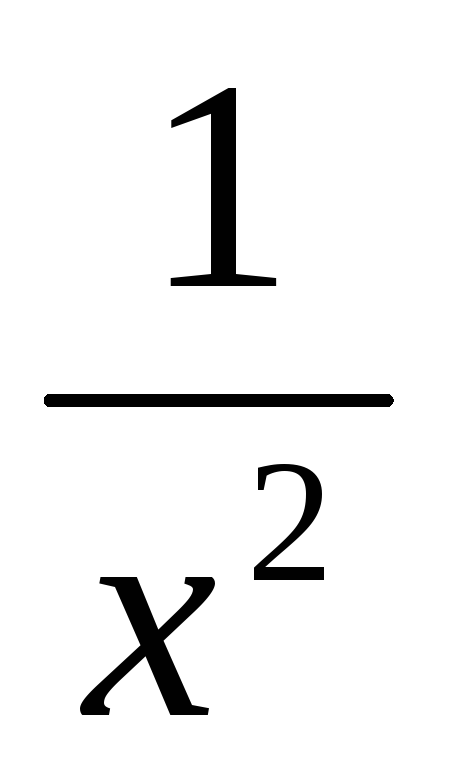
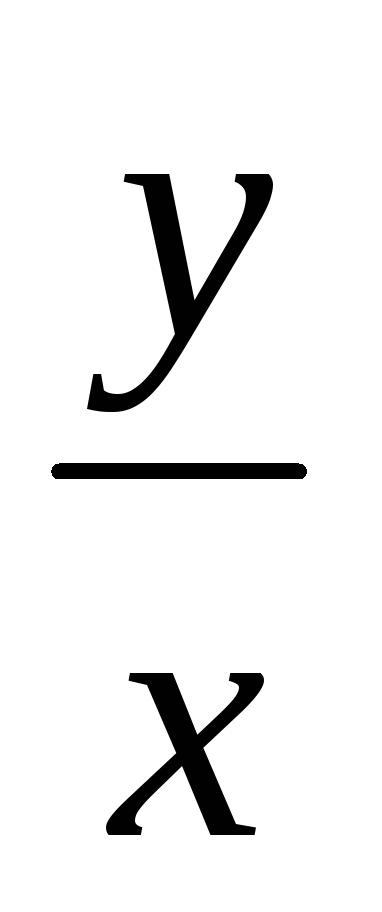
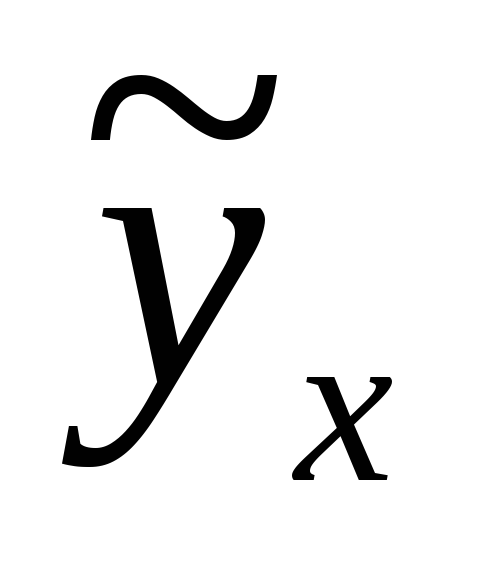
1 2 3 4 5 6 7 і т.д.
Всього

Підставивши дані таблиці 3 у рівняння, знайдемо параметри ai b.

Підставивши в рівняння, значення факторної ознаки х, дістанемо теоретичні значення результативної ознаки.

3. Тісноту зв’язку при криволінійних формах залежності визначають за допомогою кореляційного відношення:

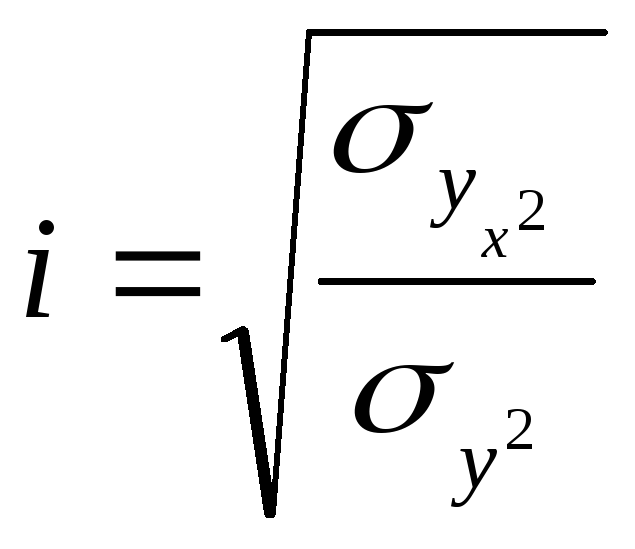
де - між групова дисперсія;

- загальна дисперсія.

Можна використати спрощену робочу формулу кореляційного відношення:

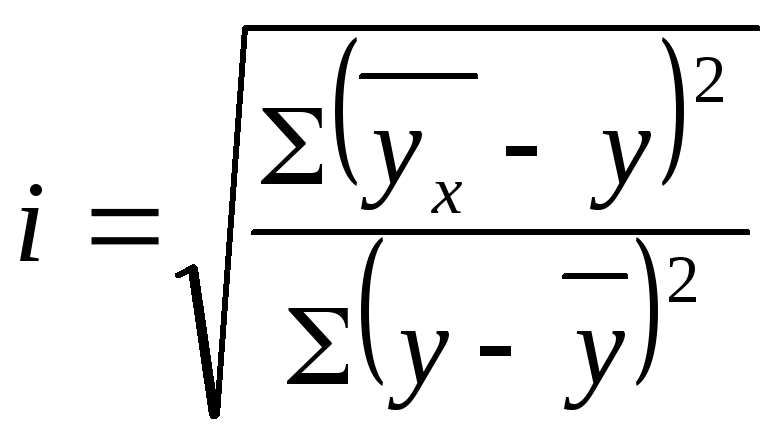
Середнє значення результативної ознаки визначають за формулою:

3. Вірогідність коефіцієнта парної кореляції визначають за t- критерієм, який обчислюють за формулою:

де - середня помилка коефіцієнта кореляції;

r- коефіцієнт кореляції;

n- вибіркова сукупність;

- фактичне значення t- критерію .

Середня помилка коефіцієнта кореляції визначається:

Якщо перевищує табличне значення, зв'язок між ознаками вірогідний. Якщо , то коефіцієнт кореляції не вірогідний. Вірогідність кореляційного відношення визначають аналогічно.