ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 19.03.2024
Просмотров: 30
Скачиваний: 0
ЗМІСТ
|
Передмова
Додатки Список літератури
|
1 2 7
10 24
29 36
42 49 55 62 69 79 85 136
|
-
Побудова епюр нормальних сил і нормальних напружень при розтягу (стиску)
Під розтягом (стиском) розуміють такий вид навантаження бруса, при якому в його поперечних перерізах виникають нормальні сили. Вважається, що нормальна сила прикладена в центрі ваги і направлена по нормалі до цього перерізу.
Передача зусиль до бруса (стержня) може бути здійснена різними способами, як показано на розрахункові схемі (рис.1.1).
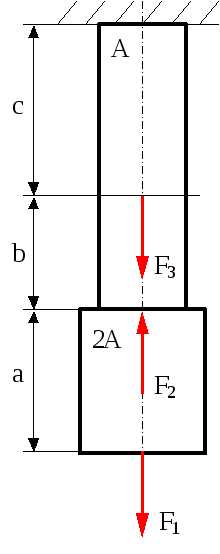
Рис.1.1
Точки прикладення сил Fi (i=1,2,3…) і лінії їх дії співпадають з віссю, яка розташована по лінії центрів ваги поперечних перерізів бруса.
При розтягу і стиску розглядаються прямолінійні стержні довільної форми поперечного перерізу А, виконані з різних матеріалів ( - питома вага матеріалів стержнів). Власна вага стержня обмежених розмірів виявляється набагато менше величини сил Fi, які можуть бути прикладені до стержнів з умови міцності матеріалів стержнів.
Нормальні сили в поперечних перерізах визначаються методом перерізів. Кожний переріз ділить стержень на дві частини. На частині, яка розглядається, додатна (розтягуюча) сила зображується від перерізу, від’ємна (стискаюча) сила – до перерізу. Дійсний напрямок нормальної сили по відношенню до перерізу встановлюється при розгляді рівноваги одної частини стержня. Для цього достатньо скласти рівняння рівноваги
F(x)=0
де x – геометрична вісь центрів ваги поперечних перерізів стержня.
Якщо в розтягнутому або стиснутому стержні його вага не враховується, то нормальні сили визначаються через задані зовнішні сили Fi.
При врахуванні власної ваги стержня нормальна сила N є функцією довжини ділянки, яка розглядається. В межах цієї ділянки поперечний переріз А може бути або постійним по величині або змінюватися по закону, який залежить від форми поперечного перерізу стержня.
В залежності від форми перерізу А вага відсіченої частини стержня може підраховуватися або в об’ємі прямокутного циліндра, квадрата і т.і. або в об’ємі піраміди, усіченого конуса і т.і.
Рівнодіюча внутрішніх сил, підрахована з врахуванням власної ваги, також прикладається в центрі ваги поперечного перерізу А.
Прийнято припущення, що в кожній точці поперечного перерізу внутрішні сили розподіляються рівномірно (принцип Сен-Венана). Ці сили, які приходяться на одиницю площі поперечного перерізу, в подальшому будемо називати нормальними напруженнями . Нормальні напруження в поперечних перерізах розтягнутого (стиснутого) стержня визначаються по формулі
![]() ,
,
де N – нормальна сила,
А – площа поперечного перерізу.
Нормальним напруженням в перерізах стержня приписуються знаки нормальних сил N в тих же перерізах.
Кожний поперечний переріз під дією нормальної сили N може переміщатися (паралельно зміщуватися відносно других поперечних перерізів) на деяку величину l (мм, см). Величина l, яка підрахована в стержнях, які виконані з машинобудівних матеріалів, мала порівняно з заданими розмірами стержнів, а тому при складанні рівнянь рівноваги в перерізах стержнів величиною l нехтують (принцип незмінності початкових розмірів).
Переріз, розташований в защемленні, не зміщується, а будь-який фіксований переріз (наприклад переріз І-І) по довжині стержня отримає по відношенню до защемлення переміщення
![]() ,
,
де l1 – відстань від перерізу І-І, який розглядається, до защемлення,
ЕА – жорсткість матеріалу стержня в межах довжини l1 (l1l, l – довжина стержня),
Е – модуль пружності матеріалу стержня.
В межах довжини l1 стержень може мати різну величину площ А (поступова або різка, ступінчаста зміна площі), а також може бути виготовлений з різних матеріалів (різні величини модуля пружності Е та питомої ваги ).
Тоді вказаний вище інтеграл для підрахунку величини lІ-І потрібно розкривати по частинам.
Якщо в підсумку отримаємо відповідь lІ-І0, то це значить, що переріз І-І віддалився від защемлення (стержень на довжині l1 отримав позитивне видовження). При lІ-І0 стержень на довжині l1 отримав деяке вкорочення (переріз І-І приблизився до защемлення відносно свого початкового положення).
В підсумку короткої теоретичної довідки відмітимо, що величини нормальних сил, нормальних напружень і переміщень поперечних перерізів стержнів від дії сил Fi і власної ваги визначаються відповідно принципу незалежності дії сил, згідно якого дія кожної сили на стержень враховується окремо, а дія всіх сил алгебраїчно сумується.
Умова міцності при розтягу (стиску)
![]() ,
,
де - напруження в поперечному перерізі стержня;
N – нормальна сила;
А – площа поперечного перерізу;
- допустиме напруження.
Умову жорсткості можна представити у вигляді
l[l],
де l – переміщення або деформація в конструкції;
[l] – допустиме значення переміщення (або деформації), яке задається згідно технічних умов експлуатації конструкції.
Приклад
Для заданого ступінчастого стержня побудувати епюри осьових зусиль з урахуванням власної ваги стержня, якщо: F1=2кН, F2=4кН, F3=3кН, А1=20см2, А2=2А1=40см2, А3=3А1=60см2, а=1м, b=1м, c=1.5м, d=0.5м, D=5см. Матеріал стержня – сталь: =78.510-3 Н/см3.
Стержень розбивається на ділянки AB, BC, CD і DE з постійною площею поперечного перерізу а також по точкам прикладення зовнішніх сил. Для визначення осьових зусиль застосовується метод перерізів. На рис.1.2,б,в,г,д показані перерізи на кожній ділянці, дію відкинутої верхньої частини замінено відповідно зусиллями N1, N2, N3 і N4. Величина цих зусиль визначається з умови рівноваги відсічених частин.
Переріз 1-1 (0x100см)
Y=0; N1-G1-F1=0,
де G1 – вага відсіченої частини першої ділянки,
![]() ,
,
N1(x=0)=A10+F1=F1=2кН=2000Н,
N1(x=100)=A1100+F1=78.510-320100+2000=2157Н,
Переріз 2-2 (0x100см)
Y=0; N2-G2-G1-F1=0,
![]() ,
,
N2(x=0)=A20+A1a+F1=78.510-3400+
+78.510-320100+2000=2157Н,
N2(x=100)=A2100+A1a+F1=78.510-340100+
+78.510-320100+2000=2471Н.